1、选择题  一根轻质弹簧，当它上端固定，下端悬挂重为G的物体时，长度为L1；当它下端固定在水平地面上，上端压一重为G的物体时，其长度为L2，则它的劲度系数是：
A．G/L1
B．G/L2
C．G/（L1-L2）
D．2G/(L1-L2)

参考答案：D

本题解析：轻质弹簧上端固定，下端悬挂重为G的物体时，弹簧的弹力大小等于G；当弹簧的下端固定在水平地面上，上端压一重为G的物体时，弹力大小等于G．根据胡克定律：弹簧的弹力与伸长的长度或压缩的长度成正比，列方程求解．
设弹簧的原长为L0，劲度系数为k，则根据胡克定律得
G=k（L1-L0）?①
G=k（L0- L2）?②
联立①②得? k=2G/(L1-L2)
故选D
点评：应用胡克定律解题时要注意弹簧的弹力与弹簧的形变量成正比，不是与弹簧的长度成正比．

本题难度：简单

2、实验题  如图所示，是用光电计时器等器材做“验证机械能守恒定律”的实验，在滑块上安装一遮光板，把滑块放在水平气垫导轨上并静止在A处，并通过定滑轮的细绳与钩码相连，光电计时器安装在B处，测得滑块（含遮光板）质量为M、钩码总质量为m、遮光板宽度为d、当地的重力加速度为g，将滑块在图示A位置释放后，光电计时器记录下遮光板通过光电门的时间为△t；

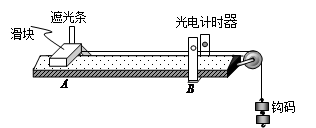
①实验中是否要求钩码总质量m远小于滑块质量M ?（填：是、否）。
②实验中还需要测量的物理量是?（用文字及相应的符号表示）。
③本实验中验证机械能守恒的表达式为: ?
（用以上对应物理量的符号表示）。
④如果实验结果系统动能增加量大于重力势能减少量，请指出实验的调节可能出的问题
??。?

参考答案：①否?②两光电门中心之间的距离L?③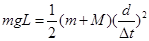?④气垫导轨不水平

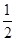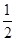本题解析：①本实验中不需要让钩码的重力等于绳子的拉力，故不要求钩码总质量m远小于滑块质量M；②为了求出运动过程中钩码减小的重力势能，则需要测量A、B间的距离L；③我们验证的是：△EP与△EK的关系，即验证：△EP=△EK代入得：mgL=(M+m)v2，而v=所以本实验中验证机械能守恒的表达式为mgL=(M+m)(()2，④如果实验结果系统动能增加量大于重力势能减少量，则可能是气垫导轨不水平造成的。

本题难度：一般

3、计算题  将质量均为m厚度不计的两物块A、B用轻质弹簧相连接，弹簧的劲度系数为k。第一次将B物块放在水平面上，A在弹簧弹力的作用下处于静止，如图（甲）所示，此时弹簧的弹性势能为Ep，现突然敲击A，使A在一瞬间获得向下的速度，在随后的过程中B物块恰能离开地面但不继续上升。第二次用手拿着A、B两物块，使得弹簧竖直并处于原长状态，此时物块B离地面的距离为H，如图（乙）所示，然后由静止同时释放A、B，B物块着地后速度立即变为0。若对于给定的弹簧，其弹性势能只跟弹簧的形变有关，求：

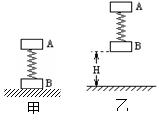
（1）第一次当B物块恰好离开地面时，A物块相对于自己静止时的初始位置升高的距离h
（2）第二次释放A、B后，A上升至弹簧恢复原长时的速度大小v1
（3）若弹簧的劲度系数k未知，但第一次敲击A后，A获得的速度大小v0已知。则第二次释放A、B后，B刚要离地时A的速度大小v2是多少？

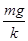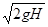参考答案：（1）2（2）（3）

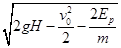
本题解析：（1）第一次静止时，弹簧向上产生的弹力与A的重力平衡。
设弹簧的形变量（压缩）为△x1，有△x1=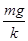? (2分)
第一次当B刚要离地时弹簧产生向上的弹力与B的重力平衡
设弹簧的形变量（伸长）为△x2，有△x2=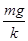? (2分)? h=△x1+△x2=2 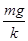(2分)
（2）第二次释放A、B后，A、B做自由落体运动，B着地后，A和弹簧相互作用至A上升到弹簧恢复原长过程中，弹簧对A做的总功为零 。?
对A从开始下落至弹簧恢复原长过程，对A由动能定理有 mgH=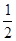mv12?(3分)
解得 v1=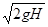? (3分)
（3）第二次释放AB后，在B刚要离地时弹簧产生向上的弹力与B的重力平衡
设弹簧的形变量（伸长）为△x3，有△x3=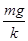?(2分)
△x1=△x2=△x3?
因此第一次静止时、第一次B刚要离地时和第二次B刚要离地时，弹簧的弹性势能都为Ep?在第一次A获得速度到B刚要离地时，对A和弹簧组成的系统，由机械能守恒有
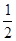mv02+Ep=mg(△x1+△x2)+EP ?(2分)
第二次释放后，对A和弹簧系统，从A上升至弹簧恢复原长到B刚要离地过程，由机械能守恒有　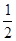　　　　　　mv12=mg△x3+EP+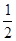mv22? (2分)
由以上解得v2=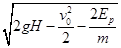　?(2分)

本题难度：一般

4、填空题  如图所示，质量相同的A、B两球用细线悬挂于天花板上且静止不动．两球间是一个轻质弹簧，如果突然剪断悬线，则在剪断悬线瞬间A球加速度为______；B球加速度为______．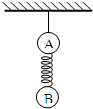

参考答案：设两球质量为m．
悬线剪断前，以B为研究对象可知：弹簧的弹力F=mg，以A、B整体为研究对象可知悬线的拉力为2mg；
剪断悬线瞬间，弹簧的弹力不变，F=mg，根据牛顿第二定律得
? 对A：mg+F=maA，又F=mg，得aA=2g，
? 对B：F-mg=maB，F=mg，得aB=0
故答案为：2g；0

本题解析：

本题难度：一般

5、实验题  在“验证机械能守恒定律”的实验中，质量为1kg的重锤自由下落，通过打点计时器在纸带上记录运动过程，打点计时器所接电源频率为50Hz．如图所示，纸带上O点为重锤自由下落时纸带打点起点，选取的计数点A、B、C、D依次间隔一个点（图中未画出），各计数点与O点距离如图所示，单位为mm，重力加速度为9.80 m/s2 ，则（答案均保留三位小数）

打点计时器记录B点时，重锤速度vB="_______" m/s，重锤动能EKB=__________J．
（2）从开始下落算起，打点计时器记录B点时，重锤势能减少量为?J．

参考答案：（1）1.175；0.690；（2）0.692。

本题解析：(1)在B点时，重锤速度vB=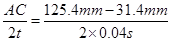="1.175" m/s，重锤动能EKB=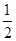mvB2=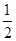×1kg×(1.175 m/s)2=0.690J。
（2）重锤势能减少量为△Ep=mgh=1kg×9.8N/kg×70.6×10－3m=0.692J。

本题难度：一般