1、选择题  为了研究太阳演化的进程需知太阳的质量，已知地球的半径为R，地球的质量为m，日地中心的距离为r，地球表面的重力加速度为g，地球绕太阳公转的周期为T，则太阳的质量为（　　）
A．

参考答案：设T为地球绕太阳运动的周期，则由万有引力定律和动力学知识得：
GMmr2=mv2r
根据地球表面的万有引力等于重力得：
对地球表面物体m′有
Gmm′R2=m′g
两式联立得M=4π2mr3T2R2g
故选A．

本题解析：

本题难度：简单

2、简答题  2008年9月我国成功发射“神舟七号”载人航天飞船．如图为“神舟七号”绕地球飞行时的电视直播画面，图中数据显示，飞船距地面的高度约为地球半径的

参考答案：
（1）设地球质量为M，半径为R，对“神舟七号”飞船由万有引力提供向心力可得：
GMmr2=mv2r，
其中：r=R+R20．
又：GM=gR2，
解得：
v=

本题解析：

本题难度：一般

3、选择题  某卫星的发射过程如图所示，先将卫星从地面发射并从A点进入椭圆轨道I运行，然后在B点通过改变卫星的速度，让卫星进入预定圆形轨道II上运行。则下列说法正确的是（?）

A．该卫星的发射速度一定要大于第二宇宙速度11.2km/s
B．该卫星沿椭圆轨道I从A点运动到B点过程中，速度减小，机械能增大
C．该卫星在轨道I上运行的周期大于在轨道II上运行的周期
D．测量出该卫星在轨道II上运行的线速度和周期，即可计算地球的质量

参考答案：D

本题解析：第一宇宙速度7.9km/s是离开地球表面的最小发射速度，第二宇宙速度11.2km/s是摆脱地球引力进入太阳系的最小发射速度，该卫星一直绕地球运动，因此发射速度在第一宇宙速度到第二宇宙速度之间，A错。根据开普勒第二定律行星和太阳连线在相等时间内扫过相等的面积，近地点A线速度大，远地点B线速度小，从A到行星B的过程线速度减小，但是万有引力也就是重力做负功，只有重力做功，机械能不变。B错。根据开普勒第三定律，所有行星绕太阳运行的半长轴的三次方与公转周期的二次方比值都相等，那么只要中心天体不变都是成立的，轨道I的半 长轴小所以周期小，C错。轨道II为匀速圆周运动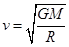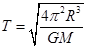，,,整理可得,答案D对。

本题难度：简单

4、简答题  两个靠得很近的天体，离其它天体非常遥远，它们以其连线上某一点O为圆心各自做匀速圆周运动，两者的距离保持不变，科学家把这样的两个天体称为“双星”，如图所示．已知双星的质量为m1和m2，它们之间的距离为L．求双星运行轨道半径r1和r2，以及运行的周期T．

参考答案：

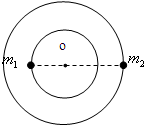
如图，
设双星中质量为m1的天体轨道半径为r1，质量为m1的天体轨道半径为r2
据万有引力定律和牛顿第二定律，得：
Gm1m2L2=m1ω2r1①
Gm1m2L2=m2ω2r2②
r1+r2=L③
由①②③联立解得：
r1=m2Lm1+m2
r2=m1Lm1+m2
再由：Gm1m2L2=m14π2T2r1得
运行的周期T=2πL

本题解析：

本题难度：一般

5、选择题  一颗小行星绕太阳做匀速圆周运动的半径是地球公转半径的4倍，则这颗小行星运转的周期是?
A．4年
B．8年
C．6年
D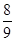．年

参考答案：B

本题解析：由周期公式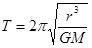可知B对；

本题难度：简单