微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 在如图所示的平面直角坐标系xOy中，存在沿x方向按如图所示规律周期性变化的匀强电场，沿x轴正向为正。沿垂直于xOy平面指向纸里的方向存在按如图所示规律周期性变化的匀强磁场，坐标原点O处有带正电的粒子，从t=0时刻无初速释放，已知粒子的质量m=5×10-10 kg，电荷量q=1×10-6 C，不计粒子的重力，求：
(1)t=0. 25×10-3 s时粒子的速度及位置；
(2)t=1×10-3 s时粒子的位置坐标；
(3)t=8×10-3 s时粒子的速度。
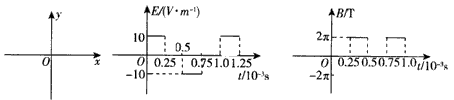
参考答案：解：(1)在第一个t0=0.25×10-3 s内粒子的加速度a满足：qE=ma
末速度v1=at0=5m/s
沿x轴正向运动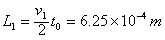
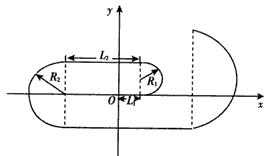
(2)0.25×10-3～0.5×10-3 s内粒子做匀速圆周运动
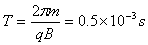
故粒子在0.25×10-3 s内运动了半个圆周
圆周运动的半径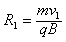
在0.5×10-3～0.75×10-3 s内粒子沿x轴负向匀加速运动
末速度大小v2=v1+at0=2v1
位移大小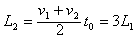
在0.75×10-3～1×10-3 s内粒子做匀速圆周运动，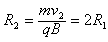
末位置坐标：x=-(L2-L1)=-1.25×10-3 m，y=-(2R2-2R1)=-8×101-4 m
(3)粒子在8×10-3 s内16次加速，每次速度增加v1，故：v=16v1
v=80 m/s，方向沿x轴正向
本题解析：
本题难度：困难
2、简答题 一个质量m=0.1g的小滑块，带有|q|=5×10-4C的电荷量多少为5×10-4C，放置在倾角α=30°的光滑斜面上（斜面绝缘），斜面置于B=0.5T的匀强磁场中，磁场方向垂直纸面向里．如图所示，小滑块由静止开始沿斜面滑下，其斜面足够长，小滑块滑至某一位置时，要离开斜面．求：
（1）小滑块带何种电荷？
（2）小滑块离开斜面的瞬时速度多大？
（3）该斜面的长度至少为多少？
参考答案：（1）小滑块沿斜面下滑过程中，受重力mg、斜面支持力N和洛伦兹力F．若要小滑块离开斜面，洛伦兹力F方向应垂直斜面向上，根据左手定则可知，小滑块应带负电荷．
（2）小滑块沿斜面下滑时，垂直斜面方向的加速度为零，有：
qvB+N-mgcosα=0
当N=0时，小滑块开始脱离斜面，此时有：qvB=mgcosα
得：v=mgcosαqB=0.1×103×10×cos30°5×10-4×0.5m/s=2
本题解析：
本题难度：一般
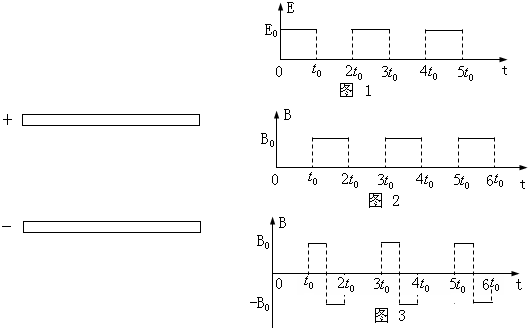
3、简答题 两块足够大的平行金属板水平放置，极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律分别如图1、图2所示（规定垂直纸面向里为磁感应强度的正方向）．在t=0时刻由负极板释放一个初速度为零的带负电的粒子（不计重力）．若电场强度E0、磁感应强度B0、粒子的比荷q/m均已知，且t0=
，两板间距h=10π2mE0
q．
（1）求粒子在0～t0时间内的位移大小与极板间距h的比值．
（2）求粒子在两极板间做圆周运动的最大半径（用h表示）．
（3）若板间电场强度E随时间的变化仍如图1所示，磁场的变化改为如图3所示，试画出粒子在板间运动的轨迹图（不必写计算过程）．
参考答案：
解法一：
（1）设粒子在0～t0时间内的位移大小为s1，由运动学公式和你对第二定律有：
s1=12at20，a=qE0m
又已知t0=2πmqB0，h=10π2mE0qB20
联立以上两式解得：
s1h=15．
（2）粒子在t0～2t0时间内只受洛伦兹力作用，且速度与磁场方向垂直，所以粒子做匀速圆周运动．设运动速度大小为v1，轨道半径为R1，周期为T，则有：
v1=at0，qv1B0=mv21R1
联立以上两式得R1=h5π
又T=2πmqB0，即粒子在t0～2t0时间内恰好完成一个周期的圆周运动．在2t0～3t0时间内，粒子做初速度为v1的匀加速直线运动，设位移为s2，则有：
s2=v1t0+12at20
解得：s2=35h
由于s1+s2＜h，所以粒子在3t0～4t0时间内继续做匀速圆周运动，设速度大小为v2，半径为R2，则有：
v2=v1+at0，qv2B0=mv22R2
解得：R2=2h5π
由于s1+s2+R2＜h，粒子恰好又能完成一个周期的圆周运动．
在4t0～5t0时间内，粒子运动到正极板（如图1所示）．因此粒子的最大半径为：
R2=2h5π．
（3）粒子在板间运动的轨迹如图2所示．
解法二：
由题意可知，电磁场的周期为2t0，前半周期粒子受电场作用做匀加速直线运动，加速度大小为：
a=qE0m，方向向上．
后半周期粒子受磁场作用多匀速圆周运动，周期为T，则有：
T=2πmqB0=t0
粒子恰好完成一次匀速圆周运动．至第n个周期末，粒子位移大小为sn，有：
sn=12a(nt0)2
又已知sn=n5πh
粒子速度大小为vn=ant0，粒子做圆周运动的半径为：
Rn=mvnqB0，
解得：Rn=nh5π，显然s2+h＜h＜s3
所以有：（1）粒子在0～t0时间内的位移大小与极板间距h的比值为s1h=15
（2）粒子在两极板间做圆周运动的最大半径R2=2h5π
（3）粒子在板间运动的轨迹图见解法一中的图2．
答：（1）粒子在0～t0时间内的位移大小与极板间距h的比值为s1h=15
（2）粒子在两极板间做圆周运动的最大半径R2=2h5π
（3）粒子在板间运动的轨迹图为图2．
本题解析：
本题难度：一般
4、选择题 如图所示，光滑绝缘杆固定在水平位置上，使其两端分别带上等量同种正电荷 ，杆上套着一带正电小球，整个装置处在一个匀强磁场中，磁感应强度方向垂直纸面向里，将靠近右端的小球从静止开始释放，在小球从右到左的运动过程中，下列说法正确的是（）
A．小球受到的洛伦兹力大小变化，但方向不变
B．小球受到的洛伦兹力将不断增大
C．小球的加速度先减小后增大
D．小球的电势能一直减小
参考答案：AC
本题解析：小球从右到左的运动过程中，小球先做加速度减小的加速运动，后做加速度增大的减速运动。小球受到的洛伦兹力大小先减小，后增大，但方向始终竖直向上。小球所受电场力先做正功，后做负功，小球的电势能先减小，后增大。
本题难度：一般
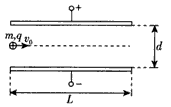
5、计算题 如图所示，两块相同的金属板正对着水平放置，金属板长为L，两板间距离为d，上极板的电势比下极板高U。质量为m、带电量为q的正离子束，沿着两板间中心轴线，以初速度v0进入两板间，最终都能从两板间射出。不计离子重力及离子间相互作用的影响。
(1)求离子在穿过两板的过程中沿垂直金属板方向上移动的距离y；
(2)若在两板间加垂直纸面的匀强磁场，发现离子束恰好沿直线穿过两板，求磁场磁感应强度B的大小和方向；
(3)若增大两板间匀强磁场的强度，发现离子束在穿过两板的过程中沿垂直金属板方向上移动的距离也为y，求离子穿出两板时速度的大小v。
参考答案：解：(1)离子在穿过两板的过程中，只受与初速度v0垂直的电场力F作用，且F=qE
两板间电场强度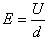
离子的加速度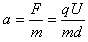
离子沿中心轴线方向做匀速直线运动，设离子穿过两板经历的时间为t，则L=v0t
离子沿垂直金属板方向上做初速度为0的匀变速直线运动，则
解得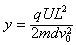
(2)离子束恰好沿直线穿过两板，说明离子受力平衡，即qE=qv0B
所以磁感应强度的大小 ，磁场的方向垂直纸面向里
(3)增大磁场的强度时，离子受洛伦兹力增大，所以离子会向上偏在离子穿过极板的过程中，电场力做负功，根据动能定理得
解得离子穿出两板时的速度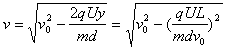
本题解析：
本题难度：困难
|
考试问吧
