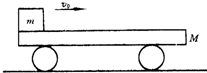
1、简答题  如图所示，质量m=20kg的物体以水平速度v0=5m/s滑上静止在水平地面的平板小车的左端．小车质量M=80kg，物体在小车上滑行一段距离后相对于小车静止．已知物体与平板间的动摩擦因数μ=0.8，小车与地面间的摩擦可忽略不计，g取10m/s2，求：
（1）物体相对小车静止时，小车的速度大小；
（2）整个过程中系统产生的热量；
（3）小车在地面上滑行的距离．

参考答案：（1）因小车与地面之间没有摩擦力，物体和车组成的系统，合外力为零，系统的动量守恒，取向右方向为正方向，根据系统的动量守恒可得，
mv0=（M+m）v共，
即20×5=（20+80）v共，
解得：v共=1m/s，即物体相对小车静止时，小车速度大小为1m/s．
（2）根据系统的能量守恒可得，
产生的热量 Q=12mv02-12（m+M）v共2=[12×20×52-12×（20+80）×12]J=200J．
（3）对小车，由动能定理可得，
W=fS=12Mv共2，
即160S=12×80×12J=40J，
所以S=0.25m，
答：（1）物体相对小车静止时，小车的速度大小是1m/s；（2）整个过程中系统产生的热量是200J；（3）小车在地面上滑行的距离是0.25m．

本题解析：

本题难度：一般

2、计算题  （5分）在光滑水平面上，一个质量为m，速度为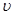的A球，与质量也为m的另一静止的B球发生正碰，若它们发生的是弹性碰撞，碰撞后B球的速度是多少？若碰撞后结合在一起，共同速度是多少？

参考答案：，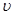

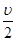
本题解析：设A、B球碰后的速度分别为v1、v2，根据动量守恒，因是弹性碰撞，故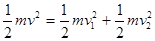，联立解得v1=0，v2=v；若碰撞后结合在一起，

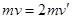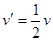
本题难度：简单

3、计算题  (9分)如图所示，质量为m1＝60 kg的小车在光滑水平面上以速度v1＝0.5 m/s向右运动，质量为m2＝40 kg的小车(包括小孩)在光滑水平面上以速度v2＝3 m/s向左运动，为了避免两滑块再次相碰，在两小车靠近的瞬间，m2上的小孩用力将m1推开．求小孩对m1做功的范围．(滑块m2与右边竖直墙壁碰撞时无机械能损失，小孩与小车不发生相对滑动，光滑水平面无限长)

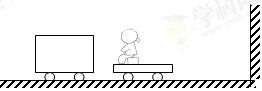
参考答案：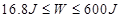

本题解析：设向左为正方向，推后二者共速向左

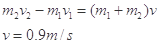
对m1分析

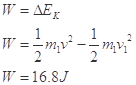
设向左为正方向，推后二者反向，速度等大


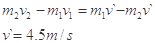
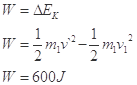
所以，做功范围为：

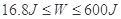
考点：原子核、动能定理、动量守恒定律

本题难度：一般

4、计算题  【选修3-5选做题】
如图所示，一辆质量mA=3kg的小车静止在光滑的水平面上，小车左端与一轻质弹簧相连，将轻质弹簧压缩并锁定，此时弹簧的弹性势能为Ep=6 J，小车上有一质量mB=1 kg的光滑小球，小球紧靠在弹簧右端，小球到小车右壁的距离L=1.2 m，现将弹簧解除锁定，小球脱离弹簧后与小车右壁的油灰阻挡层碰撞并被粘住，求：
（1）小球脱离弹簧时小球和小车各自的速度；
（2）整个过程中，小车移动的距离。

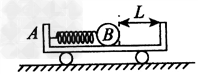
参考答案：解：（1）整个过程中，A、B和弹簧组成的系统动量守恒、机械能守恒
mAvA=mBvB

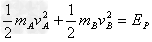
解得vA=1 m/s，vB=3 m/s
（2）设A、B移动的距离分别为LA、LB，则由动量守恒得
mALA=mBLB
又LA+LB=L
解得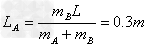

本题解析：

本题难度：一般

5、简答题  如图所示，质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂．现将绝缘球拉至与竖直方向成θ=60°的位置自由释放，下摆后在最低点与金属球发生弹性碰撞．在平衡位置附近存在垂直于纸面的磁场．已知由于磁场的阻尼作用，金属球将于再次碰撞前停在最低点处．求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°．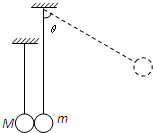

参考答案：设小球m的摆线长度为l
小球m在下落过程中与M相碰之前满足机械能守恒：mgl(1-cosθ)=12mv02①
m和M碰撞过程是弹性碰撞，故满足：
mv0=MVM+mv1 ②
12mv02=12mv12+12MVM2? ③
联立?②③得：v1=m-Mm+Mv0? ④
说明小球被反弹，且v1与v0成正比，而后小球又以反弹速度和小球M再次发生弹性碰撞，满足：
mv1=MVM1+mv2 ⑤
12mv12=12mv22+12MVM12⑥
解得：
v2=m-Mm+M|v1|?⑦
整理得：
v2=-(m-Mm+M)2v0⑧
故可以得到发生n次碰撞后的速度：
vn=|(m-Mm+M)nv0|⑨
而偏离方向为450的临界速度满足：
mgl(1-cos450)=12mv临界2⑩
联立①⑨⑩代入数据解得，当n=2时，v2＞v临界
当n=3时，v3＜v临界
即发生3次碰撞后小球返回到最高点时与竖直方向的夹角将小于45°．

本题解析：

本题难度：一般