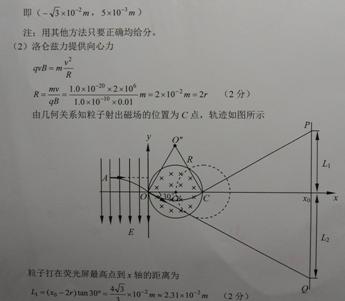
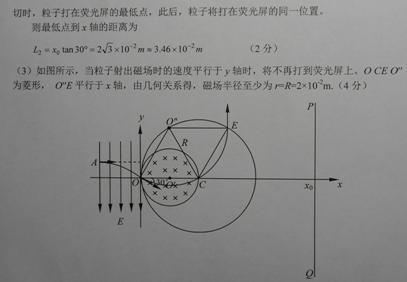
1、计算题  （16分）如图所示，xoy平面内，y轴左侧有方向竖直向下，电场强度为E=1．0×1 04 N／的匀强电场。在Y轴右侧有一个边界为圆形的匀强磁场区域，圆心O’位于x轴上,半径为r=0．01 m，磁场最左边与Y轴相切于O点，磁感应强度为B=0．01T，方向垂直纸面向里。在坐标xo=0．06m处有垂直于x轴的足够大的荧光屏PQ。一束带正电的粒子从电场中的A点（图中未标出）以垂直于电场的初速度向右运动，穿出电场时恰好通过坐标原点，速度大小为v="2" ×106m／s，方向与x轴正向成300角斜向下。已知粒子的质量为m=1．0×l0-2kg，电量为q=1．0×10-10C，重力不计。

（1）求粒子出发点A的坐标；
（2）若圆形磁场可沿x轴向右移动，圆心O仍在x轴上，由于磁场位置的不同，导致该粒子打在荧光屏上的位置也不同，求粒子打在荧光屏上的位置范围；
（3）若改变磁场半径,磁场最左边仍然与Y轴相切于O点，当磁场半径至少为多大时，粒子就再也不能打到带屏上?

参考答案：

本题解析：略

本题难度：一般

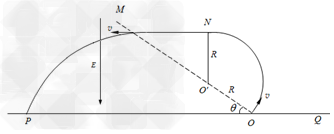
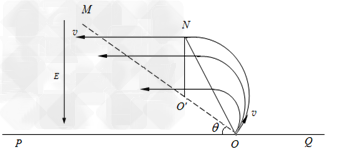
2、计算题  如图所示，在竖直平面内，虚线MO与水平线PQ相交于O，二者夹角θ=30°，在MOP范围内存在竖直向下的匀强电场，电场强度为E，MOQ上方的某个区域有垂直纸面向里的匀强磁场，磁感应强度为B，O点处在磁场的边界上，现有一群质量为m、电量为+q的带电粒子在纸面内以速度v（0<v≤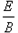）垂直于MO从O点射入磁场，所有粒子通过直线MO时，速度方向均平行于PQ向左，不计粒子的重力和粒子间的相互作用力。求：?
（1）速度最大的粒子在磁场中运动的时间；?
（2）速度最大的粒子打在水平线POQ上的位置离O点的距离；?
（3）磁场区域的最小面积。

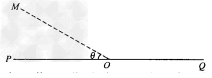
参考答案：解：（1）因粒子通过直线MO时，速度方向均平行于PQ向左，说明粒子速度方向改变了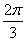，由几何关系可得粒子的运动轨迹如图所示。设粒子在匀强磁场中做匀速圆周运动的半径为R，周期为T，粒子在匀强磁场中运动时间为t1

因为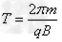
所以?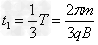
（2）由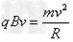，得?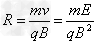
设粒子自N点水平飞出磁场，出磁场后应做匀速运动至OM，设匀速运动的距离为s，由几何关系知：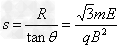
过MO后粒子在电场中做类平抛运动，设运动的时间为t2，则：?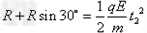
?
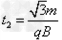由几何关系知，速度最大的粒子打在水平线POQ上的位置离O点的距离
?
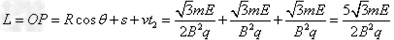（3）由题知速度大小不同的粒子均要水平通过OM，则其飞出磁场的位置均应在ON的连线上，故磁场范围的最小面积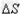是速度最大的粒子在磁场中的轨迹与ON所围成的面积

扇形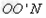的面积?
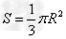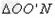的面积为：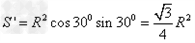

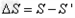
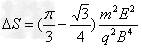
本题解析：

本题难度：困难

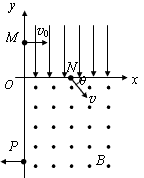
3、计算题  在平面直角坐标系xOy中，第I象限存在沿y轴负方向的匀强电场，第IV象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m，电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场，经x轴上的N点与x轴正方向成60°角射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，如图所示。不计粒子重力，求：
（1）M、N两点间的电势差UMN；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从M点运动到P点的总时间t。

参考答案：解：（1）设粒子过N点的速度为v，有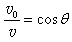，v＝2v0
粒子从M点到N点的过程，有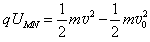
?
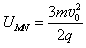
（2）粒子在磁场中以O′为圆心做匀速圆周运动，半径为O′N
有：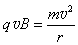
得：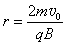
（3）由几何关系得：ON＝rsinθ
设粒子在电场中运动的时间为t1，有ON＝v0t1，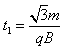
粒子在磁场中做匀速圆周运动的周期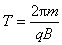
设粒子在磁场中运动的时间为t2，有，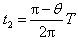
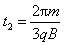
t＝t1＋t2
解得：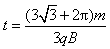

本题解析：

本题难度：困难

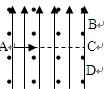
4、选择题  如图，空间某一区域内存在着相互垂直的匀强电场和匀强磁场，一个带电粒子以某一初速度由A点进入这个区域沿直线运动，从C点离开区域；如果这个区域只有电场，则粒子从B点离开场区；如果这个区域只有磁场，则粒子从D点离开场区；设粒子在上述三种情况下，从A到B点、A到C点和A到D点所用的时间分别是t1、t2和t3，比较t1、t2和t3的大小，则有(粒子重力忽略不计)? (? )

A．t1=t2=t3
B．t2<t1<t3
C．t1=t2<t3
D．t1=t3>t2

参考答案：C

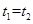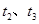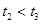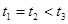本题解析：先看，由于只有电场时，电场方向与小球初速度垂直不改变A到达B点的直向速度（类似于平抛运动），再看，由于磁场不改变速度大小，A到C和D的速度大小都相同，显然A到D的距离远，即，综上，C正确，
点评：当带电粒子在电磁场中发生偏转时，需要弄清楚粒子受力情况，从而得出在各个方向上的运动性质，

本题难度：一般

5、计算题  如图14所示，在坐标系xoy的第一象限内存在匀强磁场，磁场方向垂直于xoy面向里；第四象限内有沿y轴正方向的匀强电场，电场强度大小为E。一质量为m、带电荷量为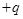的粒子自y轴的P点沿x轴正方向射入第四象限，经x轴上的Q点进入第一象限。已知P点坐标为（0，-2），Q点坐标为（4，0），不计粒子重力。求：

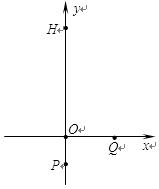
（1）求粒子过Q点时速度的大小。
（2）若磁感应强度的大小为一定值B，粒子将以垂直y轴的方向经H点进入第二象限，求B的大小及H点的坐标值；
（3）求粒子在第一象限内运动的时间t。

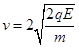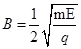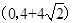参考答案：（1）?（2）??（3）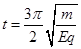

本题解析：（1）设粒子在电场中运动的时间为t0，加速度的大小为a，粒子的初速度为v0，过Q点时速度的大小为v，沿y轴方向分速度的大小为vy，在第四象限，粒子受电场力与初速度方向垂直而且为恒力，为雷平抛运动
竖直方向由牛顿第二定律得?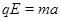?（1分）
由运动学公式得???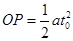
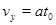水平方向?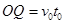
合速度?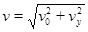
解得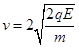：?（1分）
（2）粒子在第一象限内做匀速圆周运动，设粒子做圆周运动的半径为R，
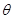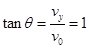第四象限类平抛运动的末速度与水平夹角为，则，即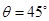
根据初末速度的洛伦兹力均指向圆心可得半径如下图所示，由几何关系可得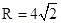?（1分）

洛伦兹力提供向心力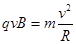?（1分）
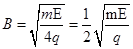解得： ?（1分）
由几何关系可得，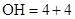
H点的坐标为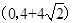?（1分）
（3）粒子在第一象限内做匀速圆周运动的圆心角为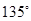，所以运动的时间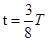
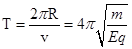?（1分）
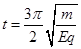解得：?（1分）

本题难度：一般