1、选择题  如图是某种正弦式交变电压的波形图，由图可确定该电压的(　　)

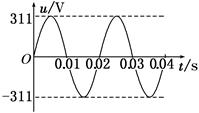
A．周期是0.01 s
B．最大值是311 V
C．有效值是220 V
D．表达式为u＝220sin 100πt(V)

参考答案：BC

本题解析：由图象知周期为0.02s，故A错误；由图象知最大值为311V，故B正确；电压的有效值为，故C正确；表达式为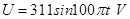，故D错误
故选：BC
点评：要根据交流电图象正确求解最大值、有效值、周期、频率、角速度等物理量，同时正确书写交流电的表达式．

本题难度：简单

2、选择题  一理想变压器原、副线圈匝数比n1∶n2＝11∶5，原线圈与正弦交流电源连接，输入电压的u－t图象如图所示，副线圈接一个10 Ω的电阻，则(　　)

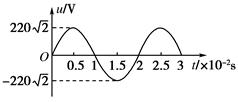
A．流过电阻的电流为0.2 A
B．与电阻并联的电压表示数是100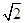V
C．变压器的输入功率是1×103 W
D．变压器副线圈中的交变电压的频率为100 Hz

参考答案：C

本题解析：原线圈电压有效值为220 V，所以副线圈的电压有效值为100 V，电阻两端的电压为100 V，流过电阻的电流为10 A，电阻的功率P＝I2R＝1000 W，则选项A、B错误，C正确．由图象可知，交流电压的周期为0.02 s，则频率为50 Hz，选项D错误．

本题难度：一般

3、简答题  如图所示，匀强磁场B=0.50 T，矩形线圈的匝数N=100，边长Lab="0.20" m，Lbc="0.10" m，以3 000 r/min的转速匀速转动,在线圈平面通过中性面时开始计时，试求：
(1)交变电动势的瞬时值表达式；
(2)若线圈总电阻为2 Ω，线圈外接电阻为8 Ω，写出交变电流的瞬时值表达式；
(3)线圈由图示位置转过的过程中，交变电动势的平均值.

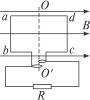
参考答案：（1）e="314sin314t" V?（2）e="31.4sin314t" A?（3）200 V

本题解析：（1）线圈的角速度：ω="2πn=314" rad/s
线圈电动势的最大值Em="NBSω=314" V
所以电动势的瞬时值表达式：e="314sin314t" V.
（2）Im=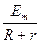="31.4" A
所以电流的瞬时值表达式：e="31.4sin314t" A.
（3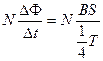）=="4NBSn=200" V.

本题难度：简单

4、选择题  如图甲所示为一发电机原理图，产生的交变电流接理想变压器的原线圈、原副线圈匝数之比为22∶1，副线圈输出的电动势e随时间t变化的规律如图乙所示，发电机线圈电阻忽略不计，则 (　　)．

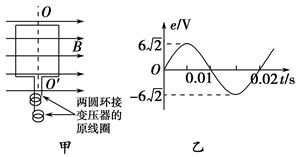
A．在t＝0.01 s时刻，穿过发电机线圈的磁通量最大
B．变压器原线圈中瞬时电动势的表达式为e′＝132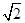sin 50πt V
C．若仅使发电机线圈的转速增大一倍，则变压器副线圈输出电压的频率增大一倍，而电压最大值不变
D．若仅使发电机线圈的转速增大一倍，则变压器副线圈输出电压的频率和最大值都增大一倍

参考答案：D

本题解析：根据题图乙可知，在t＝0.01 s时刻，变压器副线圈上产生的感应电动势的瞬时值为零，说明穿过原副线圈的磁通量的变化率为零，磁通量最大，而此时发电机线圈中的瞬时电流最大，穿过线圈的磁通量的变化率最大，磁通量为零，选项A错误；根据变压器的工作原理可知，原、副线圈中电流的周期、频率相同，根据题图乙可知，周期T＝0.02 s，角速度ω＝＝100π rad/s，所以副线圈输出的电动势e＝6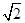sin 100πt V，原线圈输入的瞬时电动势e′＝132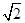sin 100πt V，选项B错误；若仅使发电机线圈的转速n增大一倍，根据关系式f＝n，ω＝2πn以及Em＝BSω可知，变压器原线圈输入电压(或副线圈输出电压)的频率和最大值都增大一倍，所以选项C错误，D正确．

本题难度：一般

5、填空题  一个矩形线圈在匀强磁场中绕垂直于磁场的转轴从中性面向开始匀速转动，在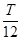(T为周期)时产牛的感应电动势为2V，则感应电动势的有效值为______V.

参考答案：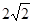

本题解析：矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动时，从中性面开始计时，线圈中感应电动势的瞬时值表达式为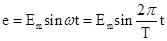，由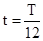?时瞬时值为2V，求出Em，再求出有效值．
解：矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动时，从中性面开始计时，线圈中感应电动势的瞬时值表达式为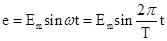．当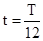时瞬时值e=2V，代入解得? Em=4V，电动势有效值。
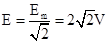点评：对于感应电动势的瞬时值表达式e=Emsinωt要注意计时起点必须是从中性面开始，否则表达式中初相位不为零．

本题难度：简单