1、简答题  一电梯，启动时匀加速上升，加速度为2m/s2，制动时匀减速上升，加速度为－1m/s2，楼高52m．求：
⑴若上升的最大速度为6m/s，电梯升到楼顶的最短时间是多少？
⑵如果电梯先加速上升，然后匀速上升，最后减速上升，全程共用时间为16s．上升的最大速度是多少？[8]

参考答案：（1）t＝13.17s
（2）上升的最大速度是4m/s

本题解析：（1）设电梯作匀加速上升的末速为v，电梯升到楼顶的总时间为t，则加速运动过程上升的位移为：
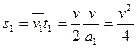，　　　　　　　　　　　　　①
减速运动过程上升的位移为：
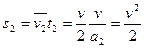，　　　　　　　　　　　　　②
匀速上升的位移为：
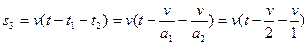，　　　　③
由题意知：
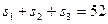，　　　　　　　　　　　　　　　④
解①、②、③、④式得：
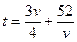，　　　　　　　　　　　　　　　　　⑤
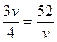从⑤式知，当，即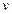=8.3m/s时，t 最短；而电梯上升的最大速度为6m/s，所以电梯升到楼顶的最短时间为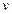=6m/s时，代入⑤式可得t＝13.17s。
(2) 如果电梯先加速上升，然后匀速上升，最后减速上升，全程共用时间为16s，代入⑤式可得v =4m/s（v =17.3m/s，不合题意舍去），故电梯上升的最大速度是4m/s。

本题难度：简单

2、选择题  如图所示，传送带的水平部分长为L，传动速率为v，在其左端无初速释放一小木块，若木块与传送带间的动摩擦因数为μ，则木块从左端运动到右端的时间不可能是（　　）
A．

2L μg D． L 2v 参考答案：①当木块一直做匀加速直线运动． 若木块一直做匀加速直线运动到达右端时的速度还未达到v． 根据牛顿第二定律得，a=μg． 根据L=12at2，解得t= 本题解析： 本题难度：简单 3、选择题  小球从空中自由下落，与水平地面第一次相碰后弹到空中某一高度，其速度随时间变化的关系如图所示，则（　　） A．小球第一次反弹初速度的大小为3m/s B．小球反弹起的最大高度为0.45m C．小球是从5m高处自由下落的 D．碰撞时速度改变量大小为2m/s

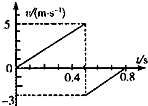
参考答案：A、由图可知，小球在t=0.3s时刻反弹，第一次反弹初速度的大小为3m/s．故A正确．
B、在0.3-0.8s内是小球第一次反弹过程，根据图象的“面积”大小等于物体在某一段时间内发生的位移可得，小球反弹起的最大高度为h=12×3×(0.8-0.5)m=0.45m．故B正确．
C、在0-0.3s内小球下落，下落的高度为H=12a1t12=12×10×（0.5）2m=1.25m．故C错误．
D、小球与地面碰撞过程的速度的变化量
△v=v2-v1=（-3）-5m/s=-8m/s．故速度的变化量大小为8m/s．故D错误．
故选AB

本题解析：

本题难度：简单

4、计算题  在一次警车A追击劫匪车B时，两车同时由静止向同一方向加速行驶，经过30 s追上。两车各自的加速度为aA＝15 m/s2，aB＝10 m/s2，各车最高时速分别为vA＝45 m/s，vB＝40 m/s，问追上时两车各行驶多少路程？原来相距多远？

参考答案：解：如图所示，以A车的初始位置为坐标原点，Ax为正方向，设L为警车追上劫匪车所走过的全程，l为劫匪车走过的全程。则两车原来的间距为ΔL＝L－l

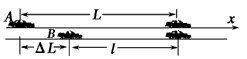
设两车加速运动用的时间分别为tA1、tB1，以最大速度匀速运动的时间分别为tA2、tB2，则vA＝aAtA1，解得tA1＝3 s，则tA2＝27 s
同理tB1＝4 s，tB2＝26 s
警车在0～3 s时间段内做匀加速运动，L1＝aAtA12
在3 s～30 s时间段内做匀速运动，则L2＝vAtA2
警车追上劫匪车的全部行程为L＝L1＋L2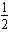＝aAtA12＋vAtA2＝1 282.5 m
同理劫匪车被追上时的全部行程为l＝l1＋l2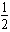＝aBtB12＋vBtB2＝1 120 m
两车原来相距ΔL＝L－l＝162.5 m

本题解析：

本题难度：困难

5、选择题  一物以6m/s的初速度在斜面上某一位置向上做加速度大小为2m/s2的匀减速运动，又以同样大小的加速度沿斜面滑下，则经过多长时间物体位移的大小为5m（斜面足够长）（　　）
A．1s
B．3s
C．5s
D．（3+

参考答案：若物体的位移在初始位置的上方，根据匀变速直线运动的位移时间公式x=v0t+12at2得，5=6t-12×2×t2，解得t=1s或t=5s．
? 若物体的位移在初始位置的下方，根据匀变速直线运动的位移时间公式x=v0t+12at2得，-5=6t-12×2×t2，解得t=3+

本题解析：

本题难度：简单