微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (10分)如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经 时间从p点射出。
时间从p点射出。
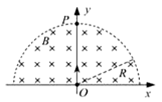
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经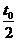 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
参考答案:(1) ,沿x轴正方向?(2)
,沿x轴正方向?(2)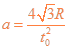 ?(3)
?(3)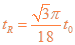
本题解析:
(1)设带电粒子的质量为m,电荷量为q,初速度为v,电场强度为E。可判断出粒子受到的洛伦磁力沿x轴负方向,于是可知电场强度沿x轴正方向
且有? qE=qvB?①
又? R=vt0?②
则? ?③
?③
(2)仅有电场时,带电粒子在匀强电场中作类平抛运动
在y方向位移?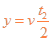 ?④
?④
由?②④式得?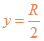 ?⑤
?⑤
设在水平方向位移为x,因射出位置在半圆形区域边界上,于是
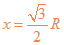
又有?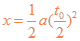 ?⑥
?⑥
得?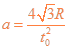 ?⑦
?⑦
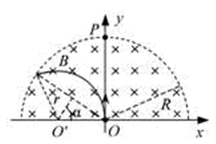
(3)仅有磁场时,入射速度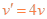 ,带电粒子在匀强磁场中作匀速圆周运动,设轨道半径为r,由牛顿第二定律有
,带电粒子在匀强磁场中作匀速圆周运动,设轨道半径为r,由牛顿第二定律有
 ?⑧
?⑧
又? qE=ma?⑨
由⑦⑧⑨式得?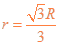 ?⑩
?⑩
由几何关系?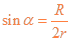 ?11
?11
即? ?
?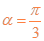 ?12
?12
带电粒子在磁场中运动周期
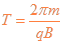
则带电粒子在磁场中运动时间
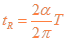
所以?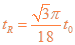 ?13
?13
本题难度:一般
2、计算题 如图所示,两平行金属板水平放置,板间存在竖直向下的勻强电场。一带电粒子以初速度V0沿上板边缘垂直于电场线射入匀强电场,它刚好贴着下板边缘飞出。已知匀强电场两极板长L,间距为d,(粒子的重力忽略不计)求:(16分)
⑴如果带电粒子的初速度变为2V0,则离开电场时,沿场强方向的侧向位移y为多少?
⑵如果带电粒子的初速度变为2V0,粒子离开电场后继续运动,当它的竖直位移仍为d时,它的水平位移x为多少?
(3)如果带电粒子的初速度变为2V0,粒子离开电场时动能与带电粒子以初速度V0射入匀强电场后离开电场时动能之比?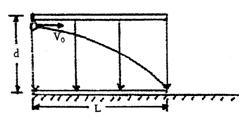
参考答案:(1) 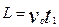 ?
?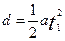 ?
?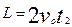 ?
?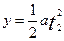 ?联立得 :
?联立得 : 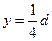
⑵ 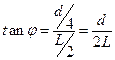 ?又?
?又?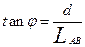 ?得
?得 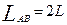 ?
?
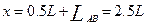
(3)?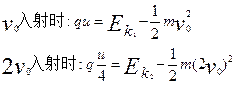 ?
?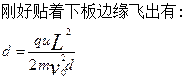
联立解得: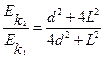
本题解析:略
本题难度:一般
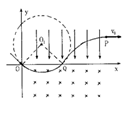
3、计算题 (16分) 如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向里的匀强磁场。现有一质量为m、电量为+q的粒子(重力不计)从坐标原点O以速度大小为v0射入磁场,其入射方向与x轴的正方向成30°角。当粒子第一次进入电场后,运动到电场中P点处时,方向与x轴正方向相同,P点坐标为〔(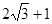 )L,L〕。(sin37°=0.6,cos37°=0.8)求:
)L,L〕。(sin37°=0.6,cos37°=0.8)求:
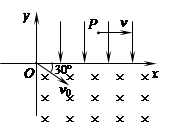
(1)粒子运动到P点时速度的大小为v;
(2)匀强电场的电场强度E和匀强磁场的磁感应强度B;
(3)粒子从O点运动到P点所用的时间t。
参考答案:(1)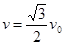 (2)
(2)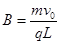 (3)
(3)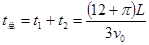
本题解析:(1)粒子运动轨迹如图所示,OQ段为圆周,QP段为抛物线,粒子在Q点时的速度
大小为v0,根据对称性可知,方向与x轴正方向成30°角,可得:?
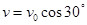 ?(2分)
?(2分)
解得: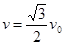 ?(1分)
?(1分)
(2)在粒子从Q运动到P的过程中,由动能定理得
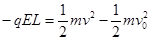 ? 2分)
? 2分)
解得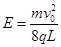 ?(1分)
?(1分)
水平方向的位移为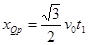 ?(1分)
?(1分)
竖直方向的位移为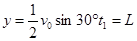 ?(1分)
?(1分)
可得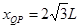 ?
?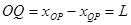 ?(1分)
?(1分)
由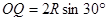 ,故粒子在OQ段圆周运动的半径
,故粒子在OQ段圆周运动的半径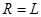 ?(1分)
?(1分)
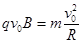 ?(2分)
?(2分)
解得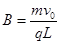 ?(1分)
?(1分)
(3)粒子从O点运动到Q所用的时间为: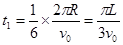 ?(1分)
?(1分)
设粒子从Q到P所用时间为t2,在竖直方向上有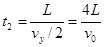 ?(1分)
?(1分)
则粒子从D点运动到P点所用的时间为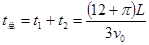 ?(1分)
?(1分)
点评:难度较大,粒子在交替复合场中的运动,首先分析粒子的受力情况,把整体的运动分解为几个分段运动,判断运动轨迹,由类平抛运动和圆周运动进行分析求解
本题难度:一般
4、计算题 (12 分)如图所示,在平面直角坐标系xOy 内,第Ⅰ象限的等腰直角三角形 MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为 m、电荷量为q的带正电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场. 已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
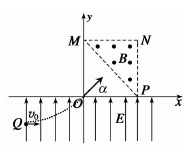
(1)电场强度E的大小;
(2)带电粒子从O点射出电场时与水平方向夹角α的正切值tan α;
(3)磁感应强度B的大小.
参考答案:(1)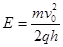 (2)
(2)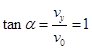 (3)
(3)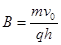
本题解析:(1)粒子在电场中运动过程中 ,由平抛运动规律及牛顿运动定律得
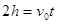 ① (1分)
① (1分)
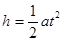 ② (1分)
② (1分)
又 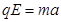 ③ (1分)
③ (1分)
联立①②③解得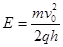 ④ (1分)
④ (1分)
(2)设粒子到达O点时的速度为v,沿y轴正方向的分速度为vy
则有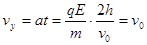 ,
,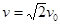 ⑤ (2分)
⑤ (2分)
速度v与x正方向的夹角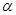 满足
满足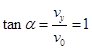 (2分)
(2分)
即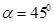 所以粒子从MP的中点垂直于MP进入磁场
所以粒子从MP的中点垂直于MP进入磁场
(3)又因为粒子垂直于NP射出磁场,所以P点为圆心
轨道半径 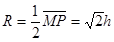 ⑥ (1分)
⑥ (1分)
由牛顿第二定律有 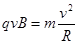 ⑦ (2分)
⑦ (2分)
将⑤⑥式代入⑦式解得 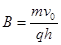 (1分)
(1分)
考点:本题考查带电粒子在复合场中的运动
本题难度:一般
5、计算题 如图所示,水平桌面处有水平向右的匀强电场,场强大小E=2´104V/m,A、B是完全相同的两个小物体,质量均为m=0.1kg,电量均为q=2´10-5C,且都带负电,原来都被按在桌面上的P点。现设法使A物体获得和电场E同方向的初速vA0=12m/s,A开始运动的加速度大小为6m/s2,经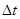 时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力,运动过程中A,B的带电量不发生改变),求:
时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力,运动过程中A,B的带电量不发生改变),求:

【小题1】小物体与桌面之间的阻力 为多大?
为多大?
【小题2】在A未与B相遇前,A电势能增量的最大值;
【小题3】如果要使A尽快与B相遇,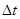 为多大?
为多大?
参考答案:
【小题1】0.2N
【小题2】4.8J
【小题3】4s
本题解析:(1)(3分)A释放后:qE+f=ma
得f=ma-qE= 0.2N
(2)(4分)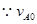 >
> ,且
,且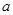 相同
相同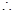 只能在A往返过程中与B相遇
只能在A往返过程中与B相遇
A速度减到零,经过的位移为s=vA02/2a=12m,tA=vA0/a=2s
DEmax=qEs=2×105×2×104×12 J=4.8J
(3)(5分)要使A在最短时间内与B相遇,则对应B减速到零时与A相遇。
B的最大位移:sB=vB02/2a=3m 运动时间:tB=vB0/a=1s
A返回时: qE-f=ma’
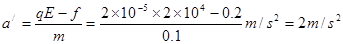
A返回走了s’=s-sB=9m 用时 ==3s
==3s 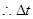 =tA+
=tA+ -tB=4s
-tB=4s
本题难度:一般