1、简答题  为满足不同列车间车厢进行重新组合的需要，通常需要将相关的列车通过“驼峰”送入编组场后进行重组（如图所示），重组后的车厢同一组的分布在同一轨道上，但需要挂接在一起．现有一列火车共有n节车厢，需要在编好组的“驼峰”左侧逐一撞接在一起．已知各车厢之间间隙均为s0，每节车厢的质量都相等，现有质量与车厢质量相等、且没有动力驱动的机车经过“驼峰”以速度v0向第一节车厢运动，碰撞后通过“詹天佑挂钩”连接在一起，再共同去撞击第二节车厢，直到n节全部挂好．不计车厢在挂接中所受到的阻力及碰撞过程所需的时间，求：
（1）这列火车的挂接结束时速度的大小；
（2）机车带动第一节车厢完成整个撞接过程所经历的时间．
（3）这列火车完成所有车厢挂接后，机车立即开启动力驱动，功率恒为P，在行驶中的阻力f恒定，经历时间t达到最大速度，求机车此过程的位移．

参考答案：（1）在车厢连接的过程中，不计车厢在挂接中所受到的阻力，动量守恒，整个挂接过程中根据动量守恒定律得：
mv0=（n+1）mv
解得：v=v0n+1
（2）与第1节车厢挂接时，根据动量守恒定律得：
mv0=2mv1
解得：v1=v02
则机车带动第一节车厢运动的时间t1=s0v1=2s0v0，
同理与第2节车厢挂接时，根据动量守恒定律得：
2mv1=3mv2
解得：v2=v03
则机车带动第一、二节车厢运动的时间t2=s0v2=3s0v0
…
同理可知机车带动n-1节车厢运动的时间为tn-1=s0vn-1=ns0v0
则总时间t=t1+t2+…+tn-1=(2+3+4+…+n)s0v0=(n+2)(n-1)s02v0
（3）当牵引力等于阻力时，速度最大，则vm=Pf，
机车开始启动到最大速度的过程中，根据动能定理得：
12mvm2-12mv2=Pt-fx
解得：x=Pt+12mv02(n+1)2-12mP2f2f
答：（1）这列火车的挂接结束时速度的大小为v0n+1；
（2）机车带动第一节车厢完成整个撞接过程所经历的时间为(n+2)(n-1)s02v0．
（3）机车此过程的位移为Pt+12mv02(n+1)2-12mP2f2f．

本题解析：

本题难度：一般

2、简答题  有一电子经电压U1加速后，进入两块间距为d，电压为U2的平行金属板间，若电子从两板正中间垂直电场方向射入，且正好能打在B板的正中点，设电子的电荷量为e，质量为m，求：
（1）电子刚进入平行金属板时的初速度v0；
（2）电子的偏转时间t．
（3）平行金属板的长度L．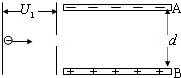

参考答案：（1）由动能定理有?eU1=12mv02
? 得?v0=

本题解析：

本题难度：一般

3、计算题  (15分)在一次国际城市运动会中，要求运动员从高为H的平台上A点，由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后落在水池中，如图所示，设滑道的水平距离为L，B点的高度h可由运动员自由调节(取g＝10m/s2)，求：

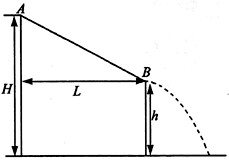
⑴运动员到达B点的速度与高度h的关系；
⑵运动员要达到最大水平运动距离，B点的高度h应调为多大？对应的最大水平距离smax为多少？
⑶若图中H＝4m，L＝5m，动摩擦因数μ＝0.2，则水平运动距离要达到7m，h值应为多少？

参考答案：⑴vB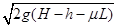＝；⑵当h＝时，smax＝H－μL＋L；⑶h1＝2.62m，h2＝0.38m

本题解析：⑴设斜面的长度为s，斜面倾角为θ，运动员到达B点的速度为vB，在运动员由A点运动至B点的过程中，运动员受重力mg、斜面的支持力N和滑动摩擦力f＝μmgcosθ作用，支持力N始终不做功，根据动能定理有：mg(H－h)－μmgcosθs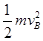＝－0?①
根据图中几何关系有：L＝scosθ?②
由①②式联立解得：vB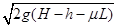＝?③
⑵运动员离开B点后做平抛运动，设经时间t落入水池，根据平抛运动规律，在水平方向有：x＝vBt ④
在竖直方向上有：h＝?⑤
运动员运动的水平距离为：s＝x＋L?⑥
由③④⑤⑥式联立解得：s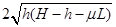＝＋L?⑦
由于h＋(H－h－μL)＝H－μL(为定值)，所以，当h＝H－h－μL，即h＝时，xmax＝H－μL
即运动员运动的最大水平距离smax＝xmax＋L＝H－μL＋L
⑶根据⑦式，当s＝7m，H＝4m，L＝5m，μ＝0.2时，解得：h1＝m＝2.62m，h2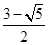＝m＝0.38m

本题难度：一般

4、计算题  如图所示，倾角为θ的光滑斜面上放有两个质量均为m的小球A、B(可视为质点)，两小球用一根长L的轻杆相连，下面的B球离斜面底端的高度为h，两球从静止开始下滑并从斜面进入光滑平面(不计与地面碰撞时的机械能损失)。求：
?
(1)两球在光滑平面上运动时的速度；
(2)在此过程中杆对A球所做的功；
(3)试用文字表述杆对A做功所处的时间段。

参考答案：（1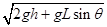）（2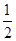）－mgLsinθ（3）从B球与地面刚接触开始至A球也到达地面的这段时间内

本题解析：(1)因系统机械能守恒有：
mgh＋mg(h＋Lsinθ)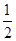＝×2mv2
解得：v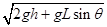＝.?（3分）
(2)以A球为研究对象，由动能定理得：
mg(h＋Lsinθ)＋W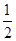＝mv2
则mg(h＋Lsinθ)＋W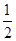＝m(2gh＋gLsinθ)
解得：W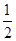＝－mgLsinθ.?（3分）
(3)从B球与地面刚接触开始至A球也到达地面的这段时间内，杆对A球做了W的负功．（2分）

本题难度：一般

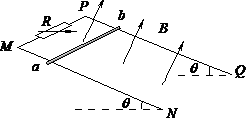
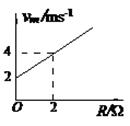
5、计算题  （10分）如图甲，MN、PQ两条平行的光滑金属轨道与水平面成θ = 30°角固定，M、P之间接电阻箱R，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B = 0.5T。质量为m的金属杆a b水平放置在轨道上，其接入电路的电阻值为r。现从静止释放杆a b，测得最大速度为vm。改变电阻箱的阻值R，得到vm与R的关系如图乙所示。已知轨距为L = 2m，重力加速度g取l0m/s2，轨道足够长且电阻不计。
（1）当R = 0时，求杆a b匀速下滑过程中产生感生电动势E的大小及杆中的电流方向；
（2）求金属杆的质量m和阻值r；
（3）当R = 4Ω时，求回路瞬时电功率每增加1W的过程中合外力对杆做的功W。

参考答案：(1)?电流方向从b→a? (2) m=0.2kg，r=2Ω? (3) W=0.6J

本题解析：（1）由图可知，当R=0时，杆最终以v=2m/s匀速运动，产生电动势
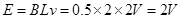?由右手定则判断可知杆中电流方向从b→a
（2）设杆运动的最大速度为v，杆切割磁感线产生的感应电动势?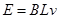
由闭合电路的欧姆定律得：,杆达到最大速度时满足?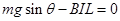
联立解得：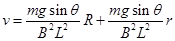
由图象可知：斜率为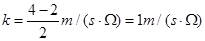，纵截距为v0=2m/s，
得到：
解得：m=0.2kg，r=2Ω?
(3)由题意：，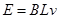
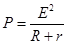
得?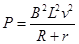
瞬时电功率增大量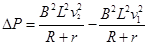
由动能定理得:?
比较上两式得?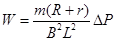
代入解得 W=0.6J

本题难度：一般