1、简答题  如图所示，一平行板电容器水平放置，板间距离为d，上极板开有一小孔，三个质量均为m、带电荷量均为+q的带电小球，其间用长为L的绝缘轻轩相连，处于竖直状态，已知?d=3L今使下端小球恰好位于小孔中，且由静止释放，让三球竖直下落．当下端小球到达下极板时，速度恰好为零．?试求：
（1）两极板间的电压?
（2）小球运动的最大速度．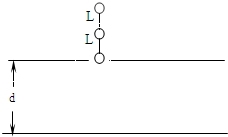

参考答案：（1）从开始到下端小球到达下极板，应用动能定理得：
? 3mgd-Eqd-Eq（d-L）-Eq（d-2L）=0 …（1）
? d=3L …（2）
而E=Ud…（3）
联立解得 U=9mgL2q?
（2）当合力为零速度最大，即3mg=EQ
由（2）（3）（4）得：E=3mg2q
联立以上两式得 Q=2q
所以第二小球进入电场时速度最大，根据动能定理得
? 3mgL-qEL=12?3mv2m
解得，vm=

本题解析：

本题难度：一般

2、简答题  如图所示，水平桌面处有水平向右的匀强电场，场强大小E=2×104V/m，A、B是完全相同的两个小物体，质量均为m=0.1kg，电量均为q=2×10-5C，且都带负电，原来都被按在桌面上的P点．现设法使A物体获得和电场E同方向的初速vA0=12m/s，A开始运动的加速度大小为6m/s2，经τ时间后，设法使B物体获得和电场E同方向的初速vB0=6m/s（不计A、B两物体间的库仑力），求：
（1）在A未与B相遇前，A电势能增量的最大值；
（2）如果要使A尽快与B相遇，τ为多大？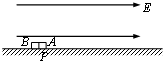

参考答案：（1）A释放后，根据牛顿第二定律有
? qE+f=ma，得f=0.2N，
A速度减到零所用时间为 t=vAOa=2s，
经过的位移为s=v2AO2a=12m，
所以在A未与B相遇前，A电势能增量的最大值为△Emax=qEs=4.8J．
（2）因为B的速度较小，要尽快相遇，对应B减速到零时与A相遇，
B的最大位移为 sB=v2BO2a=3m，花时tB=vBOa=1s，
对于A：返回时qE-f=ma′，得a′=2m/s2．
A返回走了s′=s-sB=9m，用时tA=

本题解析：

本题难度：一般

3、计算题  如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为l、足够长且电阻忽略不计，导轨平面的倾角为α，条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直。长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“”型装置，总质量为m，置于导轨上导体棒中通以大小恒为I的电流（由外接恒流源产生，图中未画出）。线框的边长为d（d＜l），电阻为R，下边与磁场区域上边界重合。将装置由静止释放，导体棒恰好运动到磁场区域下边界处返回，导体棒在整个运动过程中始终与导轨垂直，重力加速度为g。求：
（1）装置从释放到开始返回的过程中，线框中产生的焦耳热Q；
（2）线框第一次穿越磁场区域所需的时间t1；
（3）经过足够长时间后，线框上边与磁场区域下边界的最大距离xm。

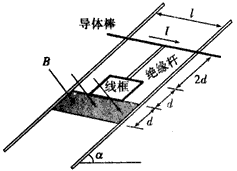
参考答案：解：（1）设装置由静止释放到导体棒运动到磁场下边界的过程中，作用在线框上的安培力做功为W
由动能定理mgsinα·4d+W－Blld=0
且Q=-W
解得Q=4mgdsinα－BIld
（2）设线框刚离开磁场下边界时的速度为v1，则接着向下运动2d
由动能定理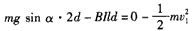
装置在磁场中运动时受到的合力F=mgsinα－F"
感应电动势ε=Bdv
感应电流I"=ε/R
安培力F"=BI"d
由牛顿第二定律，在t到t+△t时间内，有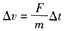
则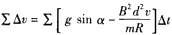
有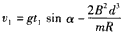
解得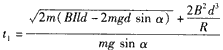
（3）经过足够长时间后，线框在磁场下边界与最大距离xm之间往复运动
由动能定理mgsinα·xm－BIl(xm－d)=0
解得

本题解析：

本题难度：困难

4、简答题  如图所示，一质量为m的物块在与水平方向成θ角的力F的作用下从A点由静止开始沿水平直轨道运动，到B点后撤去力F，物体飞出后越过“壕沟”落在平台EG段．已知物块的质量m=1kg，物块与水平直轨道间的动摩擦因数为μ=0.5，AB段长L=10m，BE的高度差h=0.8m，BE的水平距离x=1.6m．若物块可看做质点，空气阻力不计，g取10m/s2．

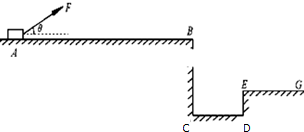
（1）要越过壕沟，求物块在B点最小速度v的大小；
（2）若θ=37°，为使物块恰好越过“壕沟”，求拉力F的大小．

参考答案：（1）设运动时间为t，则有：
h=12gt2
所以，t=

本题解析：

本题难度：一般

5、计算题  （16分）如图所示，矩形区域MNPQ内有水平向右的匀强电场；在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B。半径为R的光滑绝缘空心半圆细管ADO固定在竖直平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN。一质量为m、电荷量为q的带正电小球（可视为质点）从半圆管的A点由静止滑入管内，从O点穿出后恰好通过O点正下方的C点。已知重力加速度为g，电场强度的大小。求：

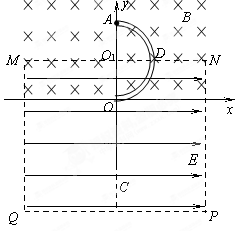
⑴小球到达O点时，半圆管对它作用力的大小；
⑵矩形区域MNPQ的高度H和宽度L应满足的条件；
⑶从O点开始计时，经过多长时间小球的动能最小？

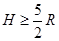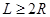参考答案：（1）?（2）?，?（3）

本题解析：⑴从A→O过程，由动能定理得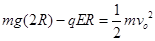：（2分）
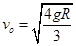解得：（1分）
在O点，由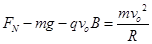（2分）?
得 ?（1分）
(2)小球从O→C 过程： 水平方向做匀减速运动，竖直方向做自由落体运动?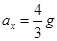
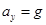
设向左减速时间为t，则?（1分）
水平位移大小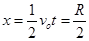（1分）?
竖直位移大小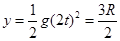（1分）
高度满足条件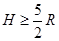（1分）?
宽度应满足条件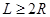（1分）
（3）以合力F方向、垂直于合力方向分别建立x-y坐标系，并将速度分别沿x、y方向分解，如图所示；当F与速度v垂直时，小球的速度最小，动能最小，设经过的时间为t，

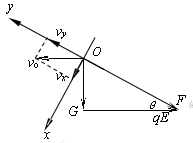
由几何关系知：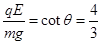
在y方向：初速度为；末速度为零；加速度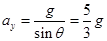
所以运动的时间

本题难度：一般