1、填空题  如图所示，半径为R的圆筒绕竖直中心轴OO/转动，小物块A靠在圆筒的内壁上，它与圆筒的动摩擦因数为μ。现要使A不下落，圆筒转动的角速度ω至少为??。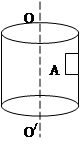

参考答案：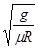

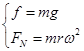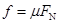本题解析：A物体不下落，说明静摩擦力等于重力，A随着转动过程中，支持力提供向心力，即，且联立则解得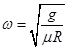
点评：本题考查了向心力的来源。通过受力分析建立等式，分析向心力来源通过向心力公式列式求解。

本题难度：简单

2、选择题  如图所示，水平转台上放着A、B、C三个物体，质量分别为2m、m、m，离转轴的距离分别为R、R、2R，与转台间的摩擦因数相同，转台旋转时，下列说法中正确的是?（?）

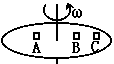
A、若三个物体均未滑动，C物体的向心加速度最大
B、若三个物体均未滑动，B物体受的摩擦力最大
C、转速增加，A物比B物先滑动
D、转速增加，C物先滑动

参考答案：AD

本题解析：
试题分析:三物都未滑动时，角速度相同，设角速度为ω，根据向心加速度公式a=ω2r，知C的向心加速度最大．故A正确；三个物体受到的静摩擦力分别为：fA=（2m）ω2R，fB=mω2R，fC=mω2（2R）．所以物体B受到的摩擦力最小．故B错误；根据μmg=mrω2得：ω=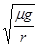，因为C物体的临界角速度最小，增加转速，可知C先达到最大静摩擦力，所以C先滑动．A、B的临界角速度相等，可知A、B一起滑动．故C错误，D正确．

本题难度：一般

3、填空题  两个完全相同的物体，分别以相同的速度，从A点和A′点进入并通过光滑圆弧轨道

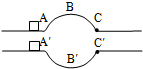
参考答案：根据动能定理知，由于轨道光滑，所以动能变化为零，到达另一端的速度与初速度大小相等，所以v1=v2．
对于沿ABC运动的物体，速度先减小后增大，沿A′B′C′运动的物体，速度先增大后减小，则沿ABC运动的平均速度小，所以运动时间长．所以t1＞t2．
故答案为：等于；大于

本题解析：

本题难度：一般

4、选择题  如上图所示，轻绳一端系一小球，另一端固定于O点，在O点正下方的P点钉一颗钉子，使悬线拉紧与竖直方向成一角度θ，然后由静止释放小球，当悬线碰到钉子时（不计任何能量损耗）则：（?）

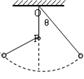
A．小球的线速度突然变大
B．小球的加速度突然变小
C．小球的角速度突然变大
D．悬线所受的拉力突然变大

参考答案：CD

本题解析：小球摆下后由机械能守恒可知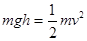，因小球下降的高度相同，故小球到达最低点时的速度相同，故小球的线速度不变，故A错误；小球的向心加速度，故小球的向心加速度增大，故B错误．根据v不变，r变小，故ω变大，故C正确；设钉子到球的距离为R，则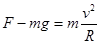，故绳子的拉力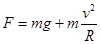因R小于L，故有钉子时，绳子上的拉力变大，故D正确；
故选CD
点评：本题中要注意细绳碰到钉子前后转动半径的变化，再由向心力公式分析绳子上的拉力变化．

本题难度：一般

5、填空题  甲、乙两物体做匀速圆周运动，其质量比是1 ∶2，运动的轨道半径之比是1 ∶2，在相等的时间里甲转了4圈，乙转了3圈。则它们所受向心力之比是_______。

参考答案：4∶9

本题解析：

本题难度：简单