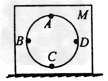
1、选择题  如图所示，质量为M的物体内有圆形轨道，质量为m的小球在竖直平面内沿圆轨道做无摩擦的圆周运动，A与C两点分别是轨道的最高点和最低点，B、D两点是圆水平直径两端点。小球运动时，物体M在地面静止，则关于M对地面的压力N和地面对M的摩擦力方向，下列说法中正确的是?

[? ]
A．小球运动到B点时，N >Mg，摩擦力方向向左?
B．小球运动到B点时，N = Mg，摩擦力方向向右?
C．小球运动到D点时，N >(M + m)g，摩擦力方向向左?
D．小球运动到C点时，N >(M + m)g，M与地面的摩擦力方向不能确定

参考答案：B

本题解析：

本题难度：一般

2、简答题  普通洗衣机的脱水桶以1200r/min的速度高速旋转，为避免发生人身伤害事故，脱水机构都装有安全制动系统．如图所示为脱水制动示意图，该系统由脱水桶盖板、制动钢丝、刹车制动盘等组成，刹车盘与脱水筒共轴转动．当脱水桶运转时，如果打开脱水桶盖，则该系统便产生制动作用．安全制动系统的作用有两个：一是将脱水电动机的电源自动切断；二是刹车带自动紧压在刹车盘上，使脱水桶迅速停止转动．
若脱水桶的半径为9cm，刹车盘的半径为6cm，打开脱水桶盖到脱水桶停止共转了50圈（设为均匀减速），若衣服和桶的质量为3kg（可以认为质量全部分布在脱水桶桶壁上，刹车盘的质量不计）．试计算：
（1）打开脱水筒盖的瞬间，贴在脱水筒筒壁上的衣服运动的线速度；
（2）刹车盘边缘上的某点在这一过程中的路程；
（3）刹车带上的平均摩擦力的大小．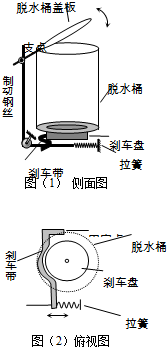

参考答案：（1）脱水桶以1200r/min的速度高速旋转，脱水桶的半径为9cm；
根据线速度公式v=rω和角速度公式联立，得到：
ω=2πnv=ωr大=2πnr大=2π×（120060）×0.09=11.31（m/s）?
（2）打开脱水桶盖到脱水桶停止共转了50圈，刹车盘的半径为6cm；
故：s=N?2πr小=50×2π×0.06=18.85（m）?
（3）脱水后，衣服紧靠脱水桶壁，桶和衣服具有动能，刹车后动能转化为内能，故：由能量守恒有：
fs=12mv2
解得：f=mv22S=3×11.3122×18.852=10.18（N）?
答：（1）打开脱水筒盖的瞬间，贴在脱水筒筒壁上的衣服运动的线速度为11.31m/s；
（2）刹车盘边缘上的某点在这一过程中的路程为18.85m；
（3）刹车带上的平均摩擦力的大小为10.18N．

本题解析：

本题难度：一般

3、选择题  如下图所示，一小球套在光滑轻杆上，绕着竖直轴OO′匀速转动，下列关于小球的说法中正确的是

[? ]
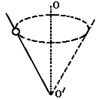
A.小球受到重力、弹力和摩擦力
B.小球受到重力、弹力
C.小球受到一个水平指向圆心的向心力
D.小球受到重力、弹力的合力是恒力

参考答案：B

本题解析：

本题难度：一般

4、简答题  带电粒子的质量m=1.7×10-27kg，电荷量q=1.6×10-19C，以速度v=3.2×106m/s沿着垂直于磁场方向又垂直磁场边界的方向进入匀强磁场，磁场的磁感应强度为B=0.17T，磁场宽度为L=10cm，求：（不计重力）．
（1）带电粒子离开磁场时的偏转角多大？
（2）带电粒子在磁场中运动的时间是多少？
（3）带电粒子在离开磁场时偏离入射方向的距离d多大？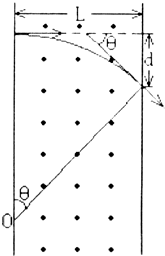

参考答案：（1）由洛伦兹力提供向心力得：
qvB=mv2?R得，
轨道半径为：R=mvqB=1.7×10-27×3.2×1061.6×10-19×0.17m=0.2m
所以，由图知　sinθ=LR=0.10.2=12
即：带电粒子离开磁场时的偏转角为：θ=30°　　
（2）带电粒子在磁场中运动的时间为：
t=θ2πT=π62π2πmqB
t=3.14×1.7×10-276×16．×10-19×0.17=3.3×10-8s
（3）由几何关系得，带电粒子在磁场中偏离入射方向的距离为：
d=R-Rcosθ
=0.2-0.2cos30°m=0.027m?
答：（1）偏转角30°（2）运动时间3.3×10-8s（3）偏离入射方向的距离0.027m

本题解析：

本题难度：一般

5、简答题  如图所示，相互平行的竖直分界面MN、PQ，相距L，将空间分为Ⅰ、Ⅱ、Ⅲ区．Ⅰ、Ⅲ区有水平方向的匀强磁场，Ⅰ区的磁感应强度未知，Ⅲ区的磁感应强度为B；Ⅱ区有竖直方向的匀强电场（图中未画出）．一个质量为m、电荷量为e的电子，自MN上的O点以初速度v0水平射入Ⅱ区，此时Ⅱ区的电场方向竖直向下，以后每当电子刚从Ⅲ区进入Ⅱ区或从Ⅰ区进入Ⅱ区时，电场突然反向，场强大小不变，这个电子总是经过O点且水平进入Ⅱ区．（不计电子重力）
（1）画出电子运动的轨迹图；
（2）求电子经过界面PQ上两点间的距离；
（3）若Ⅱ区的电场强度大小恒为E，求Ⅰ区的磁感应强度．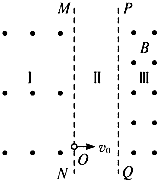

参考答案：


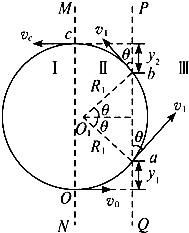
（1）电子运动的轨迹如图所示．
（2）电子在Ⅱ区Oa段做类平抛运动，
在a点的速度v1与PQ成θ角，v1sinθ=v0…①
电子在Ⅲ区ab段做匀速圆周运动，洛伦兹力提供向心力，有：
ev1B=mv21R1…②
由几何知识有：
.ab=2R1sinθ…③
①②③联立解得：
.ab=2mv0eB…④
（3）电子在Ⅱ区Oa段运动的竖直位移：
y1=12at2=eE2m?(Lv0)2=eEL22mv20…⑤
电子在bc段做类斜上抛运动，加速度与Oa段等值反向，由运动的对称性得
电子运动的竖直位移：
y2=y1=eEL22mv20…⑥
同样有对称可得电子在c处的速度为：
vc=v0，方向水平向左…⑦
所以，电子在Ⅰ区CO段做匀速圆周运动的半径为：
R′=12(y1+y2+.ab)…⑧
由牛顿运动定律有：
ev0B=mv20R′…⑨
解得：
B′=mv0mv0B+e2L2E2Emv20（或2m2v30B2m2v30+e2L2BE）
答：（1）电子运动的轨迹图如图所示．
（2）电子经过界面PQ上两点间的距离为2mv0eB．
（3）若Ⅱ区的电场强度大小恒为E，Ⅰ区的磁感应强度为mv0mv0B+e2L2E2Emv20．

本题解析：

本题难度：一般