微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 如图所示,在光滑的绝缘水平桌面上,有直径相同的两个金属小球a和b,质量分别为ma=2m,mb=m,b球带正电荷2q,静止在磁感应强度为B的匀强磁场中,不带电小球a以速度v0进入磁场,与b球发生正碰,若碰后b球对桌面压力恰好为0,求a球对桌面的压力是多大。
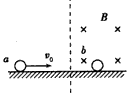
参考答案:解:a,b碰撞满足动量守恒,有2mv0=2mva+mvb ①
a与b碰后,电荷重新分配,各带电荷量为q,b对桌面恰无压力,则有mg=Bqvb ②
a受力有重力2m、支持力FN和洛伦兹力Bqva,有2mg=FN+Bqva ③
整理①②③得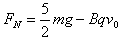
根据牛顿第三定律知,a球对桌面的压力
本题解析:
本题难度:一般
2、计算题 有一倾角为θ的斜面,其底端固定一档板,另有三个木块A、B、C,它们的质量分别为mA=mB=m,mC=3m,它们与斜面间的动摩擦因数都相同。其中木块A和一轻弹簧连接,放于斜面上,并通过轻弹簧与档板M相连,如图所示。开始时,木块A静止在P点,弹簧处于原长,木块B在Q点以初速度v0沿斜面向下运动,P、Q间的距离为l,已知木块B在下滑过程中做匀速直线运动,与木块A碰撞后立刻一起沿斜面向下运动,但不粘连,它们到达一个最低点后向上运动,木块B向上运动恰好能回到Q点。现将木块C从Q点以初速度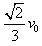 沿斜面向下运动,木块A仍静止于P点,经历同样的过程,最后木块C停在斜面上的R点(图中未画出)。求:
沿斜面向下运动,木块A仍静止于P点,经历同样的过程,最后木块C停在斜面上的R点(图中未画出)。求:
(1)A、B一起开始压缩弹簧时速度v1;
(2)A、B压缩弹簧的最大长度;
(3)P、R间的距离l"的大小。
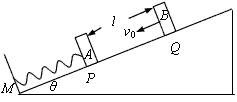
参考答案:解:(1)木块B下滑做匀速运动,有mgsinθ=μmgcosθ
B和A碰撞后,设速度为v1,根据动量守恒定律得mv0=2mv1
解得v1=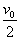
(2)设两木块向下压缩弹簧的最大长度为x,两木块被弹簧弹回到P点时的速度为v2,根据动能定理得
一μ2mgcosθ2x= 2mv
2mv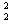 一
一 2mv
2mv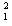
两木块在P点处分开后,木块B上滑到Q点的过程中,根据动能定理得
一(mgsinθ+μmgcosθ)l=0一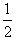 mv
mv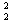
解得x=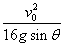 一l
一l
(3)木块C与A碰撞前后速度为v1",根据动量守恒定律得3m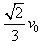 =4mv1"
=4mv1"
解得v1"=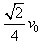
设木块C和A压缩的最大长度为x",两木块被弹簧弹回到P点时的速度为v2",根据动能定理得
一μ4mgcosθ2x"=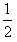 4mv"
4mv"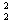 一
一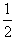 4mv"
4mv"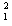
木块C与A在P点处分开后,木块C上滑到R的过程中,根据动能定理得
一(3mgsinθ+μ3mgcosθ)l"=0一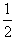 3mv"
3mv"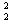
在木块压缩弹簧的过程中,重力对木块所做的功与摩擦力对木块所做的功大小相等,因此,木块B和A压缩弹簧的初动能Ek1=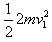 =
=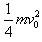
木块C与A压缩弹簧的初动能Ek2= =
=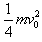
即Ek1=Ek2
因此,弹簧先后两次的最大压缩量相等,即x=x",综上可得l"=l一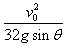
本题解析:
本题难度:困难
3、计算题 用放射源钋的α射线轰击铍时,能发射出一种穿透力极强的中性射线,这就是所谓铍“辐射”。1932年,查德威克用铍“辐射”分别照射(轰击)氢和氨(它们可视为处于静止状态)。测得照射后沿铍“辐射”方向高速运动的氨核和氦核的质量之比为7.0。查德威克假设铍“辐射”是由一种质量不为零的中性粒子构成的,从而通过上述实验在历史上首次发现了中子。假设铍“辐射”中的中性粒子与氢或氦发生弹性正碰,试在不考虑相对论效应的条件下计算构成铍“辐射”的中性粒子的质量。(质量用原子质量单位u表示,1 u等于1个12C原子质量的十二分之一。取氢核和氦核的质量分别为1.0 u和14 u。)
参考答案:解:设构成铍“辐射”的中性粒子的质量和速度分别为m和v,氢核的质量为mH。构成铍“辐射”的中性粒子与氢核发生弹性正碰,碰后两粒子的速度分别为v"和vH"
由动量守恒与能量守恒定律得:mv=mv′+mHvH′
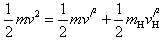
解得:
同理,对于质量为mN的氮核,其碰后速度为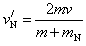
可求得: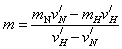
根据题意可知:vH′=7.0vN′
解得:m=1.2u
本题解析:
本题难度:困难
4、计算题 (选修3-5选做题)
质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地面上,钢板处于平衡状态。一质量也为m的物块甲从钢板正上方距离为h的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们一起向下运动x0后到达最低点B;若物块乙质量为2m,仍从A处自由落下,则物块乙与钢板一起向下运动到B点时,仍具有向下的速度,求此时速度的大小vB(已知重力加速度为g)。
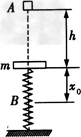
参考答案:解:设物块甲刚落在钢板上时的速度为v0,根据机械能守恒定律可得:
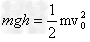
解得: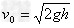
设物块甲与钢板碰撞后的速度为v1,根据动量守恒定律可得:
mv0=2mv1
解得: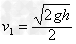
根据题意可知到达最低点占时弹簧的弹性势能增为:
设当物块乙落在钢板上时的速度为v"0,根据机械能守恒定律可得:
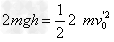
解得: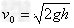
设物块乙与钢板碰撞后的速度为v2,根据动量守恒定律可得:
2mv"0=3mv2
解得: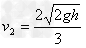
根据能量守恒定律可得:
由以上各式解得: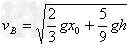
本题解析:
本题难度:一般
5、计算题 (15分)两个质量都是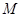 =0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为
=0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为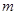 =0.1kg的子弹以
=0.1kg的子弹以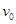 =140m/s的水平速度射向
=140m/s的水平速度射向 ,如图所示.射穿
,如图所示.射穿 后,进入
后,进入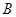 并同
并同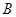 一起运动,测得
一起运动,测得 、
、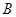 落点到桌边缘的水平距离
落点到桌边缘的水平距离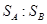 =1∶2,求:
=1∶2,求:
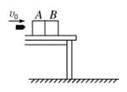
(1)沙箱 离开桌面的瞬时速度;(2)子弹在砂箱
离开桌面的瞬时速度;(2)子弹在砂箱 ?
?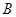 中穿行时系统一共产生的热量
中穿行时系统一共产生的热量 .
.
参考答案:(1)  ?(2)
?(2) 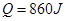
本题解析:(1)在子弹穿过A和B的过程中,A、B和子弹组成的系统满足动量守恒定律
设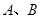 离开桌面的瞬时速度分别为
离开桌面的瞬时速度分别为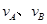 ,则
,则 ?①
?①
离开桌面后,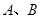 分别做平抛运动,则
分别做平抛运动,则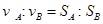 ?②
?②
联立①②解得 ,
,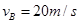
(2)子弹在砂箱 中穿行的过程,系统满足能量守恒则:
中穿行的过程,系统满足能量守恒则: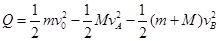 ?③
?③
解得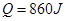
本题难度:困难