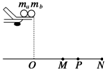
1、填空题  如图所示“为探究碰撞中的不变量”的实验装置示意图．
（1）本实验中，实验必须要求的条件是______
A．斜槽轨道必须是光滑的
B．斜槽轨道末端点的切线是水平的
C．入射小球每次都从斜槽上的同一位置无初速释放
D．入射球与被碰球满足ma＞mb，ra=rb
（2）如图，其中M、P、N分别为入射球与被碰球对应的落点的平均位置，则实验中要验证的关系是______
A．ma?ON=ma?OP+mb?OM
B．ma?OP=ma?ON+mb?OM
C．ma?OP=ma?OM+mb?ON
D．ma?OM=ma?OP+mb?ON．

参考答案：（1）A、“验证动量守恒定律”的实验中，是通过平抛运动的基本规律求解碰撞前后的速度的，只要离开轨道后做平抛运动，对斜槽是否光滑没有要求，故A错误；
B、要保证每次小球都做平抛运动，则轨道的末端必须水平，故B正确；
C、要保证碰撞前的速度相同，所以入射球每次都要从同一高度由静止滚下，故C正确；
D、为了保证小球碰撞为对心正碰，且碰后不反弹，要求ma＞mb，ra=rb，故D正确．
故选BCD．
（2）要验证动量守恒定律定律即：mav0=mav1+mbv2
小球做平抛运动，根据平抛运动规律可知根据两小球运动的时间相同，上式可转换为：
mav0t=mav1t+mbv2t
故需验证maOP=maOM+mbON，因此ABD错误，C正确．
故选C．

本题解析：

本题难度：一般

2、计算题  【选修3-5选做题】
如图所示，两块长度均为d＝0.2m的木块A、B，紧靠着放在光滑水平面上，其质量均为M＝0.9kg。一颗质量为m＝0.02kg的子弹（可视为质点且不计重力）以速度v0＝500m／s水平向右射入木块A，当子弹恰水平穿出A时，测得木块的速度为v＝2m／s，子弹最终停留在木块B中。求：?
（1）子弹离开木块A时的速度大小及子弹在木块A中所受的阻力大小；?
（2）子弹和木块B的最终速度大小。

参考答案：解：（1）设子弹离开A时速度为v1，对子弹和A、B整体，有：
mvo=mv1+2Mv?
Fd=mvo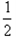2-mv1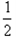2-2Mv2
以上联合解得：v1=320m/s，F=7362N
（2）子弹在B中运动过程中，最后二者共速，速度设为v2，对子弹和B整体，有
mv1+Mv=（m+M）v2?
解得：v2=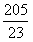≈8.9m/s

本题解析：

本题难度：一般

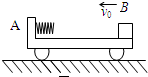
3、简答题  如图所示，质量为M的小车A左端固定一根轻弹簧，车静止在光滑水平面上，一质量为m的小物块B从右端以速度v0冲上小车并压缩弹簧，然后又被弹回，回到车右端时刚好与车保持相对静止．求：
（1）这过程弹簧的最大弹性势能EP为多少？
（2）全过程系统摩擦生热Q多少？

参考答案：（1）全过程系统动量守恒，小物块将弹簧压缩到最短和被弹回到车右端的两个时刻，系统的速度是相同的，设向左为正方向：
mv0=（M+m）v
由于两个时刻速度相同，说明小物块从车左端返回车右端过程中弹性势能的减小恰好等于系统内能的增加，即弹簧的最大弹性势能Ep恰好等于返回过程的摩擦生热，而往返两个过程中摩擦生热是相同的，所以EP是全过程摩擦生热Q的一半，Q=2EP
全过程由能量守恒和转过定律得：
Q=12mv02-12（M+m）v2
联立得：EP=Mmv024(m+M)
Q=Mmv022(m+M)
答：（1）这过程弹簧的最大弹性势能EP为Mmv024(m+M)；
（2）全过程系统摩擦生热Q为Mmv022(m+M)．

本题解析：

本题难度：一般

4、计算题  火车车厢之间由车钩连接，火车起动前车钩间都有间隙。不妨将火车的起动简化成如图所示的情景：在光滑水平面上有19个静止的质量均为m的木箱，自右向左编号依次为0、1、2、3、……18，相邻木箱之间由完全非弹性的钩子连接，当钩子前后两部分相碰时，与钩子相连的两木箱速度立即变为相等。所有木箱均静止时，每一个车钩前后两部分间的距离都为L。
（1）若只给第0号木箱一个水平向右的初速度υ0，求第18号木箱刚运动时速度的大小；
（2）若从某时刻开始，持续对第0号木箱施加向右的水平恒力F，使木箱从静止开始运动，求
（i）第1号木箱刚运动时速度的大小；
（ii）从施加恒力F到第18号木箱开始运动经历的时间。

参考答案：解：（1）19个木箱相互作用过程满足动量守恒定律，即mυ0=19mυ18
得第18号木箱刚运动时速度的大小υ18=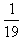υ0
（2）（i）若给第0号木箱施加恒定的水平拉力F，第0、1号木箱相互作用前，第0号木箱做匀加速直线运动，加速度大小为a0=
因为υ0′2=2a0L
得第0、1号木箱相互作用前瞬间第0号木箱的速度υ0′
第0、1号木箱相互作用过程满足动量守恒定律，即mυ0′=2mυ1
解得第1号木箱刚运动时速度的大小υ1=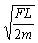
（ii）第1号木箱刚运动时速度的大小(2υ1)2=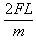 ①
第1号木箱与第2号木箱作用前的速度υ1′，有υ1′2－υ12=2a1L
又第1号木箱的加速度大小a1=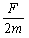
第1、2号木箱相互作用过程满足动量守恒定律，2mυ1′=3mυ2
得第2号木箱刚运动时速度的大小υ2满足(3υ2)2=(2υ1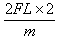)2+ ②
同理得第3号木箱刚运动时速度的大小υ3满足(4υ3)2=(3υ2)2+ ③
……
第18号木箱刚运动时速度的大小υ18满足(19υ18)2=(18υ17)2+ ④
累加可得第18号木箱刚运动时速度的大小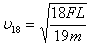
对所有木箱，根据动量定理得Ft=19mυ18
得所求时间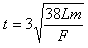

本题解析：

本题难度：困难

5、选择题  如图所示，三辆完全相同的平板小车a、b、c成一直线排列，静止在光滑水平面上，c车上有一小孩跳到b车上，接着又立即从b车跳到a车上，小孩跳离c车和b车时对地的水平速度相同，他跳到a车上没有走动便相对a车静止.此后（?）

A．a、c两车运动速率相同
B．三辆车运动速率关系为vc＞va＞vb
C．a、b两车运动速度相同
D．a、c两车运动方向相同

参考答案：B

本题解析：设人的质量为m，对地速度为v0，车的质量为M.人从c车跳出有：0=mv0-Mvc
人跳到b车再跳出，有mv0=Mvb+mv0
人跳上a车，有mv0=(M+m)va，可得vc＞va＞vb.

本题难度：简单