1、计算题  如图，质量为M=60 kg的高山滑雪运动员，从A点由静止开始沿雪道滑下，从B点水平飞出后又落在与水平面成倾角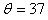°的斜坡上C点。已知AB两点间的高度差为h=25 m，B、C两点间的距离为S=75 m，（g取10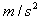，）求：
（1）运动员从B点飞出时的速度的大小；
（2）运动员从A到B过程中克服摩擦力所做的功。

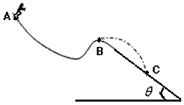
参考答案：解：（1）水平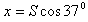位移，竖直位移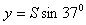，运动员从B到C做平抛运动，根据平抛运动规律得：
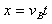? ①
? ?②
? 联立①②解得
（2）运动员从A到B过程中克服摩擦力所做的功为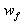，根据动能定理得：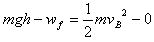
? 代入数据解得：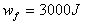

本题解析：

本题难度：困难

2、简答题  

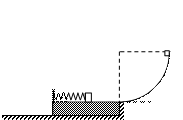
如图所示，物块C质量mc=4kg，上表面光滑，左边有一立柱，放在光滑水平地面上；一轻弹簧左端与立柱连接，右端与物块B连接，mB=2kg；竖直放置的半径R=1.8m的光滑四分之一圆弧最低点的切线水平，且与物块C上表面在同一水平面。物块A从圆弧的顶点静止释放，达到最低点时炸裂成质量m1=2kg，m2=1kg的两个物块1和2，物块1水平向左运动与B粘合在一起，物块2具有水平向右的速度，刚好回到圆弧的最高点。A、B都可以看着质点。取g=10?m/s2。求：
(1) 物块A炸裂时增加的机械能△E是多少？
(2) 在以后的过程中，弹簧最大的弹性势能Epm是多大？
(3) 从弹簧开始被压缩到被压缩到最短的过程中，物块B对弹簧做的功W是多少？

参考答案：（1）108 J ?（2）36?J?（3）54?J

本题解析：(1)设物块A炸裂前的速度为v0，由动能定理

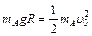
设物块1的初速度为v1，物块2的初速度为v2，则v2=v0
mAv0= m1v1－m2v2
mA=m1+m2?解得v1=12m/s
?
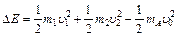解得△E ="108" J
(2) 设物块1与B粘合在一起的共同速度为vB，由动量守恒
m1v1=(m1+mB)vB
vB="6" m/s
在以后的过程中，当物块C和1、B的速度相等时，弹簧的弹性势能最大，设共同速度为vm，由动量守恒? (m1+mB)vB=(m1+mB+mC)vm
vm="3" m/s
由能量守恒得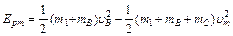
Epm= 36?J
（3）从弹簧被压缩到被压缩到最短的过程中，根据功能关系有

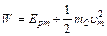
W="54?J"

本题难度：一般

3、计算题  

质量为8×107kg的列车，从某处开始进站并关闭发动机，只在恒定阻力作用下减速滑行。已知它开始滑行时的初速度为20m/s，当它滑行了300m时，速度减小到10m/s，接着又滑行了一段距离后刚好到达站台停下，那么：
（1）关闭动力时列车的初动能为多大？
（2）列车受到的恒定阻力为多大？
（3）列车进站滑行的总时间为多大？

参考答案：解：（1）列车的初动能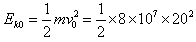J=1.6×1010 J
（2）由动能定理有：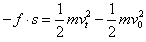
解得列车受到的阻力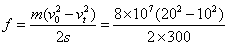N=4×107N
（3）由动量定理有：-ft=mvt-mv0
解得列车滑行的总时间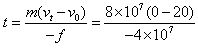s=40 s

本题解析：

本题难度：一般

4、计算题  (15分)如图所示，两带有等量异种电荷的平行金属板M、N竖直放置，两板间的距离d＝0.4m，现将一质量m＝1.0×10－2kg、电荷量q＝＋4×10－5C的带电小球从两极板上方A点，以v0＝2m/s的初速度水平抛出，A点距离两板上端的高度h＝0.2m，之后小球恰从M板顶端位置无碰擦地进入板间，做直线运动，直至打在N板上的B点，设空气阻力不计，g＝10m/s2，匀强电场只存在于M、N之间，求：

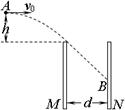
⑴小球进入电场时的速度大小和方向；
⑵两极板间的电势差U；
⑶小球到达B点时的动能。

参考答案：⑴v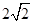＝m/s，方向与水平方向成45°角斜向下；⑵U＝1000V；⑶EkB＝0.12J

本题解析：⑴小球开始时做平抛运动，设小球进入电场时的速度大小为v，方向与水平方向间的夹角为θ，根据动能定理有：mgh＝－
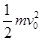
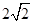解得：v＝＝m/s＝m/s
根据几何关系有：cosθ＝＝，即θ＝45°
⑵由于小球进入电场后做直线运动，因此所受合力方向与速度方向共线，即所受电场力方向只能水平指向N板，所以有：＝mgtanθ
解得两极板间的电势差为：U＝＝1000V
⑶对全程，根据动能定理有：mg(h＋dtanθ)＋qU＝EkB－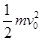
解得：EkB＝mg(h＋dtanθ)＋qU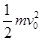＋＝0.12J

本题难度：一般

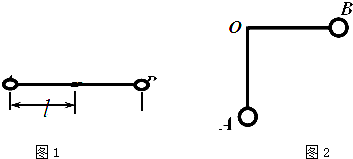
5、简答题  如图1所示，在竖直向下，场强为E的匀强电场中，长为2l的绝缘轻杆可绕固定轴O在竖直平面内无摩擦转动，两个小球A、B固定于杆的两端，A、B的质量分别为m1和m2，A带负电，电量为q1，B也带负电，电量为q2．求：
（1）杆从静止开始由水平位置顺时针转到竖直位置，在此过程中电场力所做的功为多少？
（2）杆从静止开始由水平位置顺时针转到竖直位置时，两球的总动能为多少？
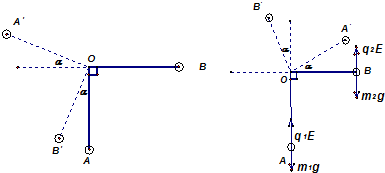
（3）若将轻杆弯折成如图2所示的“Γ”形，两边互相垂直、长度均为l，在竖直向下的匀强电场中（场强E的大小未知），可绕过O点的水平轴在竖直平面内无摩擦转动．现将“Γ”形杆从OB位于水平位置由静止释放，OB杆能转过的最大角度为127°，则该电场强度的大小为多少？

参考答案：（1）电场力做功大小W=Eq1l-Eq2l?
（2）对系统研究，根据动能定理得：（ q1-q2）El+（m2-m1）g l=Ek-0
解得：Ek=（?q1-q2）El+（m2-m1）g?l?
（3）OB杆可能顺时针转动，也可能逆时针转动．当OB杆转过最大角度时，动能为零．
（ⅰ）设OB杆顺时针转动，根据动能定理，
（m2g-q2?E）l?cosα-（?q1E-m1g）l（1+sinα）=0
解得：E=m2-2m1q2-2q1g＜m2gq2
讨论：由于使OB杆顺时针转动，
必须满足m2g＞q2E，


所以：E=m2-2m1q2-2q1g＜m2gq2
即：m2-2m1q2-2q1-m2q2＜0
2(m2q1-m1q2)q2(q2-2q1)＜0
当q2＞2q1，m1m2＞q1q2时，顺时针转动，当?q2＜2q1，m1m2＜q1q2时，顺时针转动．
（ⅱ）设OB杆逆时针转动，根据动能定理，
（q2E-m2?g）lcosα+（q1E-m1g）l（1+sinα）=0
解得：E=m2+2m1q2+2q1g＞m2gq2
讨论：由于使OB杆逆时针转动，必须满足m2g＜q2E，
所以：E=m2+2m1q2+2q1g＞m2gq2
即：m2+2m1q2+2q1-m2q2g＞0
2(m1q2-m2q1)gq2(q2+2q1)＞0
当?m1q2＞m2q1时，即当?m1m2＞q1q2时杆逆时针转动．
答：（1）杆从静止开始由水平位置顺时针转到竖直位置，在此过程中电场力所做的功为Eq1l-Eq2l．
（2）两球的总动能为（ q1-q2）El+（m2-m1）g l．
（3）当顺时针转动时，该电场强度的大小为m2-2m1q2-2q1g，逆时针转动时，电场强度的大小为m2+2m1q2+2q1g．

本题解析：

本题难度：一般