1、实验题  如图13-7-8所示，边长为L的等边三角形三个顶点a、b、c处在匀强电场中，且电场线与a、b、c共平面.一个电子只在电场力作用下由a运动到b动能减少了ΔEk，而一个质子只在电场力作用下由a运动到c动能增加了ΔEk，则电场强度的大小为________.

图13-7-8

参考答案：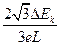

本题解析：由题意可知b、c两点在同一个等势面上，由动能定理W＝ΔEk及W＝qU，得eELsin60°=ΔEk，则E=.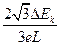

本题难度：简单

2、简答题  如图1所示，真空中存在电场强度E=1.5×103V/m、方向竖直向上的匀强电场．在电场中固定有竖直面内的光滑绝缘轨道ABC，其中AB段水平，BC段是半径R=0.5m的半圆，直径BC竖直．有两个大小相同的金属小球1和2（均可视为质点），小球2的质量m2=3×10-2kg、电量q=+2×10-4C，静止于B点；小球1的质量m1=2×10-2kg、不带电，在轨道上以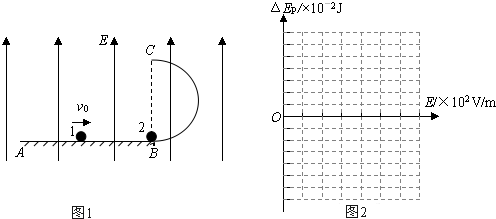初速度v0=

参考答案：（1）设两小球碰撞后的速度速度分别为v1、v2，则
m1v0=m1v1+m2v2
弹性碰撞，无机械能损失，故：
12m1v20=12m1v21+12m2v22
解得：
v2=2m1v0m1+m2=2×2×10-2×52

本题解析：

本题难度：一般

3、填空题  两个点电荷固定于x轴上，电量大小分别为Q和4Q，在它们形成的电场中，有一个带正电的试探电荷q从无限远处移向坐标原点O，其电势能EP随位置变化的关系如图所示曲线．当x→0时，电势能EP→∞；当x→∞时，电势能EP→0；电势能为最小值的位置坐标为x0．试根据图线提供的信息，确定在x轴的正半轴上各点场强方向为______；这两个点电荷在x轴上的位置是______．

参考答案：（1）根据正电荷在电势高处电势能大，可知，带正电的试探电荷从远处移近x0的过程中，电势能减小，电势降低，所以电场的方向指向x的负方向；从x0移动到x=0的过程中，电势能增大，电势升高，所以电场的方向指向x正方向．所以：在x轴的正半轴上各点场强方向为：：（0～x0）x正方向?（x0～+∞）x负方向．
（2）由图知，EP-x图象的斜率△EP△x=F=qE，则知x0点场强为零．
两个点电荷的合场强为0，说明两个点电荷一定是一正一负；当x→0时，电势能EP→∞；说明了x=0处一定是正电荷．
由E=kQr2和（1）中已经判断出的场强的方向，可以进一步判定，正电荷的电荷量一定是Q，离开x 0点的距离近；负电荷的电荷量是4Q．
由E=kQr2得：r1r2=

本题解析：

本题难度：一般

4、简答题  如图所示，在厚铅板A表面中心放置一很小的放射源，可向各个方向放射出速率为v0的α粒子（质量为m、电荷量为q），在金属网B与A板间加有竖直向上的匀强电场，场强为E，A与B间距为d，B网上方有一很大的荧光屏M，M与B间距为L.当有α粒子打在荧光屏上时就能使荧光屏产生一闪光点，整个装置放在真空中，不计重力的影响.试分析：

（1）打在荧光屏上的α粒子具有的动能有多大？
（2）荧光屏上闪光点的范围有多大？
（3）在实际应用中，往往是放射源射出的α粒子的速率未知.请设计一个方案，用本装置来测定α粒子的速率.

参考答案：(1)qEd+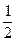mv02
(2)
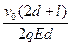
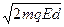
(3)见解析

本题解析：（1）qEd=EkB-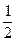mv02得EkB=qEd+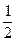mv02.
（2）α粒子初速度与电场方向垂直时，做类平抛运动，沿场强方向：a=qE/m.d=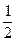at2,得到达B板的时间t1=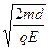?粒子具有沿场强方向的速度vBy=at=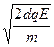.从B板到M板所用时间为
t2==·.
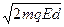粒子运动总时间t=t1+t2=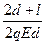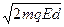,荧光屏上闪光范围是个圆，其半径
R=v0t=.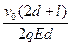
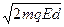（3）测出荧光屏上闪光范围的半径R，v0=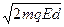.或将AB间电场反向，调节电场强度，当荧光屏上闪光消失时，α粒子初动能完全用来克服电场力做功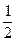，mv02=qE′d得v0=

本题难度：一般

5、简答题  如图9所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场I和II，两电场的边界均是边长为L的正方形（不计电子所受重力）。?
小题1:在该区域AB边的中点处由静止释放电子，?求电子离开ABCD区域的位置。
小题2:在电场I区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置。
小题3:若将左侧电场II整体水平向右移动L/n（n≥1），?
仍使电子从ABCD区域左下角D处离开（D不随电场移动），求在电场I区域内由静止释放电子的所有位置。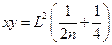

参考答案：
小题1:坐标为（－2L，）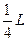
小题2:xy＝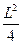
小题3: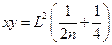

本题解析：小题1:设电子的质量为m，电量为e，电子在电场I中做匀加速直线运动，出区域I时的为v0，此后电场II做类平抛运动，假设电子从CD边射出，出射点纵坐标为y，有
?
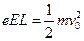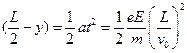
解得　y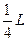＝，所以原假设成立，即电子离开ABCD区域的位置坐标为（－2L，）
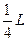小题2:设释放点在电场区域I中，其坐标为（x，y），在电场I中电子被加速到v1，然后进入电场II做类平抛运动，并从D点离开，有


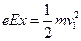
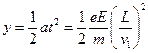
解得　xy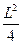＝，即在电场I区域内满足议程的点即为所求位置。
小题3:设电子从（x，y）点释放，在电场I中加速到v2，进入电场II后做类平抛运动，在高度为y′处离开电场II时的情景与（2）中类似，然后电子做匀速直线运动，经过D点，则有?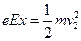
，
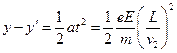
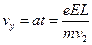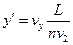
解得　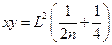，即在电场I区域内满足议程的点即为所求位置

本题难度：简单