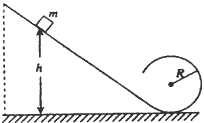
1、计算题  如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道与之相切的圆形轨道连接而成，圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动。要求物块能通过圆形轨道最高点，且在该最高点与轨道间的压力不能超过5mg（g为重力加速度）。求物块初始位置相对于圆形轨道底部的高度h的取值范围。

参考答案：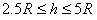

本题解析：

本题难度：困难

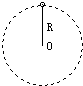
2、选择题  如图所示，用细绳拴着质量为m的物体，在竖直平面内做半径为R的圆周运动，则下列说法正确的是（　　）
A．小球过最高点时，绳子张力可以为零
B．小球过最高点时的速度是0
C．小球做圆周运动过最高点时的最小速度是

参考答案：A、小球过最高点绳子的拉力为零时，速度最小，根据mg=mv2R得，v=

本题解析：

本题难度：一般

3、填空题  如图，光滑的

参考答案：机械能守恒定律可得：
mgR=12mv2，
解得：
v2=2gR，
故此时向心加速度为：
a=v2R=2g，
而小球过B点后做平抛加速度为重力加速度g，
故在B处前后的瞬间小球的加速度大小之比为：
2g：g=2：1．
故答案为：2：1．

本题解析：

本题难度：一般

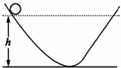
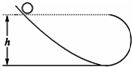
4、选择题  如图所示，A、B、C、D四图中的小球以及小球所在的左侧斜面完全相同，现从同一高度h处由静止释放小球，使之进入右侧不同的竖直轨道：除去底部一小圆弧，A图中的轨道是一段斜面，高度大于h；B图中的轨道与A图中轨道相比只是短了一些，且斜面高度小于h；c图中的轨道是一个内径略大于小球直径的管道，其上部为直管，下部为圆弧形，与斜面相连，管的高度大于h；D图中的轨道是个半圆形轨道，其直径等于h，如果不计任何摩擦阻力和拐弯处的能量损失，小球进入右侧轨道后能到达h高度的是（　　）
A．

B．

C．

D．

参考答案：A、小球到达最高点的速度可以为零，根据机械能守恒定律得，mgh+0=mgh′+0．则h′=h．故A正确．
? B、小球离开轨道做斜抛运动，运动到最高点在水平方向上有速度，即在最高点的速度不为零，根据机械能守恒定律得，mgh+0=mgh′+12mv2．则h′＜h．故B错误．
? C、小球离开轨道做竖直上抛运动，运动到最高点速度为零，根据机械能守恒定律得，mgh+0=mgh′+0．则h′=h．故C正确．
? D、小球在内轨道运动，通过最高点有最小速度，故在最高点的速度不为零，根据机械能守恒定律得，mgh+0=mgh′+12mv2．则h′＜h．故D错误．
故选AC．

本题解析：

本题难度：简单

5、选择题  如图所示，在第一象限内有垂直纸面向里的匀强磁场，正、负电子分别以相同速度沿与x轴成30°角的方向从原点垂直磁场射入，则负电子与正电子在磁场中运动时间之比为（　　）
A．1：