微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
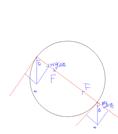
1、简答题 某平面上有一半径为R的圆形区域,区域内、外均有垂直于该平面的匀强磁场,圆外磁场范围足够大,已知两部分磁场方向相反,方向如图所示,磁感应强度都为B,现在圆形区域的边界上的A点有一个电量为q,质量为m的带正离子沿半径方向射入圆内磁场.求:
(1)若离子的速度大小为v1,求该离子在磁场中的轨道半径r;
(2)若离子与圆心O的连线旋转一周时,离子也恰好回到A点,试求该离子的运动速度v;
(3)在离子恰能回到A点的情况下,该离子回到A点所需的最短时间t.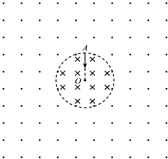
参考答案:
(1)由?Bqv=mv2r?得r=mvqB?①
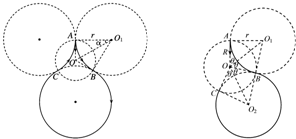
(2)如图,O1为粒子运动的第一段圆弧AB的圆心,O2为粒子运动的第二段圆弧BC的圆心,如右图所示,根据几何关系可知?tanθ=rR?②
∠AOB=∠BOC=2θ,如果粒子回到A点,则必有?n×2θ=2π,(n=3,4,5…)③
由①②③可得v=qBRmtanπn,(n=3,4,5…)
(3)粒子做圆周运动的周期T=2πmqB
因为粒子每次在圆形区域外运动的时间和圆形区域内运动的时间互补为一个周期T,所以粒子穿越圆形边界的次数越少,所需时间就越短,因此取n=3,
其轨迹如左图所示,代入到③可得θ=π3?而粒子在圆形区域内运动的圆弧的圆心角为α=π3
故所求的粒子回到A点的最短运动时间?t=T+α2πT=7πm3qB.
答:(1)若离子的速度大小为v1,该离子在磁场中的轨道半径r是mvqB;
(2)若离子与圆心O的连线旋转一周时,离子也恰好回到A点,该离子的运动速度v是qBRmtanπn,(n=3,4,5…);
(3)在离子恰能回到A点的情况下,该离子回到A点所需的最短时间t是7πm3qB.
本题解析:
本题难度:一般
2、选择题 质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直放置,开口向上,滑到最低点时速度大小为V,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是

[? ]
A. 受到向心力为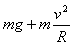
B. 受到的摩擦力为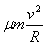
C. 受到的摩擦力为μmg
D 受到的合力方向斜向左上方
参考答案:D
本题解析:
本题难度:简单
3、选择题 如图(a)所示,小球与轻绳—端相连,绕另—端点O在竖直平面内作圆周运动,忽略一切阻力的影响,现测得绳子对小球的拉力随时间变化的图线如图(b)所示,则小球处于最高点位置的时刻是(?)
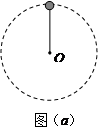

A.t1
B.t2
C.t3
D.t4
参考答案:D
本题解析:竖直平面内圆周运动过程中半径方向的合外力提供向心力,圆心以上的位置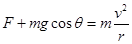 ,最高点速度最小,
,最高点速度最小,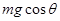 最大,此时,F最小。圆心以下的位置
最大,此时,F最小。圆心以下的位置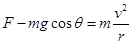 ,最低点速度最大,
,最低点速度最大,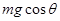 最大,F最大,所以最高点位置绳子拉力最小。所以答案D对。
最大,F最大,所以最高点位置绳子拉力最小。所以答案D对。
本题难度:一般
4、简答题 在平面直角坐标系xOy中,第I象限存在沿y轴负方向的匀强电场,第IV象限存在垂直于坐标平面向外的匀强磁场,磁感应强度大小为B.一质量为m,电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角离开电场,同时射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.(不计粒子重力)试求:
(1)粒子离开电场时的速度大小;
(2)M、N两点间的电势差UMN;
(3)P点到坐标原点O的距离OP.
参考答案:(1)
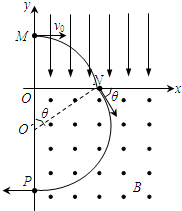
粒子垂直于电场进入第一象限,粒子做类平抛运动,将到达N点的速度分解得知
? vcosθ=v0,
解得,粒子离开电场时的速度大小v=2v0.
(2)从M→N过程,由动能定理得
? qUMN=12mv2-12mv20
代入解得,UMN=3mv202q
(3)粒子进入第四象限后,在洛伦兹力的作用下做匀速圆周运动,则
? qvB=mv2R
得粒子在磁场中做圆周运动的轨道半径为 R=mvqB=2mv0qB.
画出轨迹如图,由几何知识得
? OP=R+Rcosθ=3mv0qB
答:
(1)粒子离开电场时的速度大小是2v0;
(2)M、N两点间的电势差UMN为3mv202q.
(3)P点到坐标原点O的距离OP是3mv0qB.
本题解析:
本题难度:一般
5、简答题 电子扩束装置由电子加速器、偏转电场和偏转磁场组成.偏转电场由加有电压的相距为d的两块水平平行放置的导体板组成,匀强磁场的左边界与偏转电场的右边界相距为s,如图甲所示.大量电子(其重力不计)由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间射入偏转电场.当两板没有加电压时,这些电子通过两板之间的时间为2t0,当在两板间加如图乙所示的周期为2t0、幅值恒为U0的电压时,所有电子均从两板间通过,进入水平宽度为l,竖直宽度足够大的匀强磁场中,最后通过匀强磁场打在竖直放置的荧光屏上.问:
(1)如果电子在t=0时刻进入偏转电场,则离开偏转电场时的侧向位移大小是多少?
(2)电子在刚穿出两板之间的偏转电场时最大侧向位移与最小侧向位移之比为多少?
(3)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多少?(已知电子的质量为m、电荷量为e)
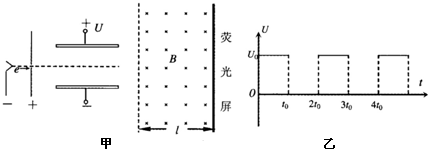
参考答案:(1)当电子在t=0时刻进入偏转电场时,侧向位移大小为
y=12at20+vyt0=12πU0emdt20+U0emdt0?t0
得y=3U0et202dm
(2)由题意可知,要使电子的侧向位移最大,应让电子从0、2t0、4t0…等时刻进入偏转电场,在这种情况下,电子的侧向位移为
ymax=y=12at20+vyt0,
得 ymax=3U0et202dm
要使电子的侧向位移最小,应让电子从t0、3t0…等时刻进入偏转电场,在这种情况下,电子的侧向位移为
? ymin=12at20
解得,ymin=U0e2dmt20
所以最大侧向位移和最小侧向位移之比为ymax:ymin=3:1
(3)设电子从偏转电场中射出时的偏向角为θ,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径R,由几何关系有:
? R=lsinθ
设电子从偏转电场中出来时的速度为vt,垂直偏转极板的速度为vy,则电子从偏转电场中出来时的偏向角为:sinθ=vyvt
式中?vy=U0edmt0
又?R=mvtBe?
由上述四式可得:B=U0t0dl
答:(1)电子在t=0时刻进入偏转电场,则离开偏转电场时的侧向位移大小是3U0et202dm.
(2)电子从两平行板间射出时最大侧向位移与最小侧向位移之比是3:1.
(3)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为U0t0dl.
本题解析:
本题难度:一般