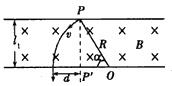
1、简答题  在平面直角坐标系xOy中，第Ⅰ象限存在沿y轴正方向的匀强电场，场强大小为E．第Ⅲ、第Ⅳ象限-d≤y≤0内存在垂直于坐标平面向内的匀强磁场．一质量为m、电荷量为-q的带负电的粒子从y轴上的M点以速度υ0垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ=60°角射入磁场，恰好不会从磁场的下边界射出磁场，如图所示．不计粒子的重力，求
（1）M、N两点间的电势差U；
（2）磁场的磁感应强度大小B；
（3）粒子从M点运动到第一次离开磁场的总时间t．

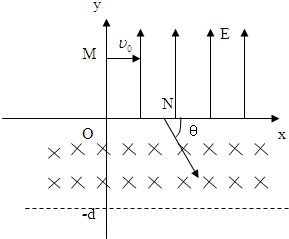
参考答案：（1）粒子离开第一象限的电场时，粒子速度v=v0cos60°=2v0，
电子在电场中做类平抛运动，
由动能定理得：qU=12mυ2-12mυ20，
解得：U=3mv202q；
（2）粒子在磁场中做匀速圆周运动，运动轨迹如图所示，
由数学知识可得：rsin30°+r=d，
由牛顿第二定律得：qBv=mv2r，
解得：B=3mυ0qd；
（3）粒子在磁场中做圆周运动的周期：T=2πrqB=2πmqB，
由粒子在磁场中的运动轨迹，由数学知识可得，粒子转过的圆心角为240°，
粒子在磁场中的运动时间：t2=240360T，
粒子离开电场时竖直方向的分速度vy=vsin60°=

本题解析：

本题难度：一般

2、简答题  如图所示，有一对平行金属板，两板相距为0.05m．电压为10V；两板之间有匀强磁场，磁感应强度大小为B0=0.1T，方向与金属板面平行并垂直于纸面向里．图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为B=

参考答案：（1）离子在平行金属板之间做匀速直线运动，洛仑兹力与电场力相等，即：
B0qv=qE0，
E0=Ud
解得：v=2000m/s
（2）在圆形磁场区域，离子做匀速圆周运动，由洛仑兹力公式和牛顿第二定律有：
Bqv=mv2r
由几何关系有：tanθ2=Rr
离子的比荷为：qm=2×104C/kg
（3）弧CF对应圆心角为θ，离子在圆形磁场区域中运动时间t，
t=θ2π?T
T=2πmqB
解得：t=θB0RdUtanθ2=

本题解析：

本题难度：一般

3、计算题  如图所示，条形区域AA"BB"中存在方向垂直于纸面向外的匀强磁场，磁感应强度B的大小为0.3 T，AA"，BB"为磁场边界，它们相互平行，条形区域的长度足够长，宽度d=1 m。一束带正电的某种粒子从AA"上的O点以沿着与AA"成60°角、大小不同的速度射入磁场，当粒子的速度小于某一值v0时，粒子在磁场区域内的运动时间t0=4×10-6 s；当粒子速度为v1时，刚好垂直边界BB"射出磁场，取π≈3，不计粒子所受重力，求：
(1)粒子的比荷。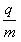
(2)速度v0和v1的大小。

参考答案：解：(1)若粒子的速度小于某一值v0时，则粒子不能从BB"离开磁场区域，只能从AA"边离开，无论粒子速度大小，在磁场中运动的时间相同，轨迹如图所示（图中只画了一个粒子的轨迹）

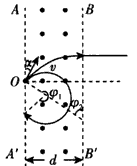
粒子在磁场区域内做圆周运动的圆心角均为φ1=240°
运动时间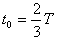
又
解得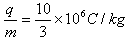或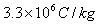
(2)当粒子速度为v0时，粒子在磁场内的运动轨迹刚好与BB"边界相切，此时有R0+R0sin30°=d
又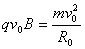
得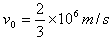
当粒子速度为v1时，刚好垂直边界BB"射出磁场区域，此时轨迹所对圆心角φ2=30°，有R1sin30°=d
又
得v1=2×106m/s

本题解析：

本题难度：困难

4、简答题  如图在宽度分别为l1和l2的两个毗邻的条形区域中分别有匀强磁场和匀强电场，磁场方向垂直于纸面向里，电场方向与电、磁场分界线平行向右．一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场，然后以垂直于电、磁场分界线的方向进入电场，最后从电场边界上的Q点射出．已知PQ垂直于电场方向，粒子轨迹与电、磁场分界线的交点到PQ的距离为d．不计重力，求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比．

参考答案：粒子在磁场中做匀速圆周运动（如图）．由于粒子在分界线处的速度与分界线垂直，圆心O应在分界线上，OP长度即为粒子运动的圆弧的半径R．由几何关系得



R2=l12+（R-d）2 ①
设粒子的质量和所带正电荷分别为m和q，由洛伦兹力公式和牛顿第二定律得
qvB=mv2R? ②
设P"为虚线与分界线的交点，∠POP"=α，则粒子在磁场中的运动时间为
t1=Rαv? ③
式中sinα=l1R? ④
粒子进入电场后做类平抛运动，其初速度为v，方向垂直于电场．设粒子加速度大小为a，由牛顿第二定律得
qE=ma ⑤
由运动学公式有
d=12at22?⑥
l2=vt2 ⑦
式中t2是粒子在电场中运动的时间
由①②⑤⑥⑦式得EB=l21+d2l22v? ⑧
由①③④⑦式得t1t2=l21+d22dl2arcsin(2dl1l21+d2)?
答：电场强度与磁感应强度大小之比为l21+d2l22v，粒子在磁场与电场中运动时间之比为l21+d22dl2arcsin(2dl1l21+d2)．

本题解析：

本题难度：一般

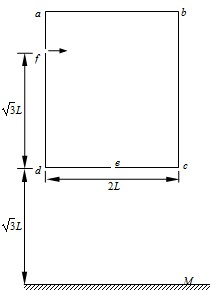
5、简答题  如图所示，abcd是一个长方形盒子，在ad边和cd边上各开有小孔f和e，e是cd边上的中点，荧光屏M平行cd放置，能显示从e孔射出的粒子落点位置．盒子内有一方向垂直于abcd平面的匀强磁场，磁感应强度大小为B．粒子源不断地发射相同的带电粒子，粒子的初速度可以忽略．粒子经电压为U的电场加速后，从f孔垂直于ad边射入盒内，再经磁场偏转后恰好从e孔射出．若已知fd=

参考答案：（1）带电粒子在电场中加速．根据动能定理得：
qU=12mv2
解得：
v=

本题解析：

本题难度：一般