1、综合题  读“地球的公转”图，图中字母表示地球在公转轨道上的位置（阴影部分表示夜半球，如C处北极圈内出现极昼现象），请用字母回答：（6分）

（1）金湖县正午太阳高度最小的位置是________。
（2）金湖县处于秋季的位置是________。
（3）淮安市白昼最长的位置是________。
（4）全球昼夜等长，且太阳直射点将要向南半球移动的是________。
（5）远日点附近是________。
（6）近日点附近是________。

参考答案：
（1）? A
（2） D
（3） C <

本题解析：
（1）本题考查正午太阳高度的变化规律。金湖县正午太阳高度最小时为冬至日，位置是A。
（2）D位于秋分日，金湖县处于秋季。
（3）夏至日淮安白昼时间最长。
（4）秋分日，太阳直射赤道，全球昼夜等长，且太阳直射点将要向南半球移动。
（5）远日点为7月初，接近于E位置。
（6）近日点为1月初，接近于F位置。

本题难度：简单

2、单选题  北京和上海两地的自转角速度和线速度比较，正确的是
A．两地的自转角速度和线速度都相同
B．两地的自转角速度和线速度都不同
C．线速度相同，角速度北京大于上海
D．角速度相同，线速度北京小于上海

参考答案：D

本题解析：试题分析：地球自转角速度规律：除南北两极外，自转角速度处处相等；自转线速度规律：自赤道向两极递减，故北京和上海的自转角速度相同，而北京的纬度较上海高，故线速度较上海小。
点评：本题难度低，学生只要掌握地球自转角速度和线速度的变化规律，结合上海和北京两地的纬度位置分析即可。

本题难度：简单

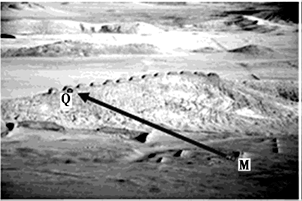
3、单选题  昌克罗十三塔位于秘鲁沿海沙漠地带的一座矮山山顶，呈南北方向排列，每座塔东西两侧各有一个观测点。2012年6月20日6时28分（地方时）在Q观测点看到太阳在M点方向的地平线上，2012年夏至日为6月21日。读图完成下列问题。
1.M点位于Q观测点的2.下列关于昌克罗地区在未来两个月内昼夜长短状况及正午十三塔影子长短变化的叙述，正确的是

A.西北方向
B.西南方向
C.东南方向
D.东北方向
E.昼长夜短逐渐变长
F.昼短夜长先变长后变短
G.昼长夜短逐渐变短
H.昼短夜长先变短后变长

参考答案：1. D
2. B

本题解析：试题分析：
1.2012年6月20日太阳直射在北半球，日出方位为东北，6时28分（地方时）在Q观测点看到太阳在M点方向的地平线上，正值日出，M点位于Q观测点的东北方向，故答案选D。
2.昌克罗地区位于南半球，这一年夏至日为6月21日，在未来两个月内太阳始终直射在北半球，该地昼短夜长，当日为6月20日，夏至日6月21日正午十三塔影子达到最长，随后随着太阳直射点南移，正午十三塔影子逐渐变短，故答案选B。
考点：本题考查地球运动的地理意义。

本题难度：简单

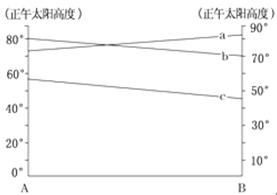
4、单选题  下图中的a、b、c分别表示地球上A、B两条纬线间北半球夏至日、春秋分日和冬至日时的正午太阳高度变化情况。读图，回答小题。
1.图中A纬线和B纬线所表示的纬度分别是2.当图中A纬线被晨昏圈分割的昼弧与夜弧等长时，则此时北京天安门广场旗杆在日出、正午、日落时的影子朝向依次是

A.10°N与20°N
B.20°N与30°N
C.0°与10°S
D.10°S与20°S
E.正东、正南、正西
F.正西、正北、正东
G.东北、正北、西北
H.西南、正南、东南

参考答案：1. A
2. B

本题解析：试题分析：
1.从图中可知夏至日A地正午太阳高度约为730左右，春秋二分日约800，冬至日约770；B地正午太阳高度约为830左右，春秋二分日约700，冬至日约470；根据正午太阳高度=900-│当地地理纬度±太阳直射点纬度│，可得出A为10°N、B为20°N?，A对。也可以分析，春秋二分日正午太阳高度分别是800和700，可知纬度分别为10°和20°，夏至日的太阳高度都比冬至日大，可见AB两地都在北半球。
2.“当图中A纬线被晨昏圈分割的昼弧与夜弧等长时”说明昼夜平分，A地不在赤道上，昼夜平分说明太阳直射赤道，全国都东升西落，北京天安门广场太阳日出、正午、日落分别在正东、正南、正西，旗杆在日出、正午、日落时的影子朝向依次是正西、正北、正东（影子方向与日出方向相反），A对。
考点：本题考查正午太阳高度计算应用、太阳视运动与影子。

本题难度：简单

5、单选题  假如黄赤交角减小到20°，那么地球上的五带的变化情况是

A.热带范围将扩大，
B.温带范围将缩小
C.寒带范围将缩小
D.温带范围无变化

参考答案：C

本题解析：试题分析：黄赤交角变小，则回归线度数变小，则热带范围变小；而极圈度数与黄赤交角度数互余，故极圈度数变大，则极圈到极点的范围即寒带的范围变小，则温带的范围变大。
考点：本题考查黄赤交角对五带的影响。
点评：本题解题关键是掌握黄赤交角与回归线和极圈的度数关系。

本题难度：一般