微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2014硕士研究生入学考试数学一真题及答案
一、选择题1—8小题.每小题4分,共32分.
1.下列曲线有渐近线的是( )
(A)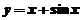 (B)
(B)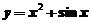 (C)
(C)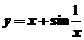 (D)
(D)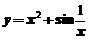
2.设函数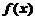 具有二阶导数,
具有二阶导数,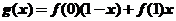 ,则在
,则在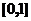 上( )
上( )
(A)当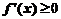 时,
时,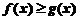 (B)当
(B)当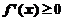 时,
时,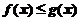
(C)当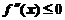 时,
时,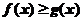 (D)当
(D)当 时,
时,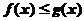
3.设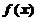 是连续函数,则
是连续函数,则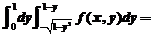 ( )
( )
(A)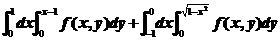
(B)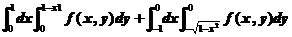
(C)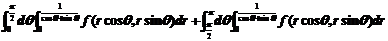
(D)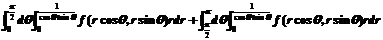
4.若函数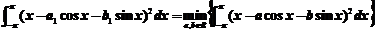 ,则
,则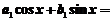 ( )
( )
(A) (B)
(B) (C)
(C)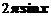 (D)
(D)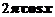
5.行列式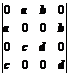 等于( )
等于( )
(A)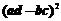 (B)
(B)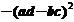 (C)
(C)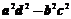 (D)
(D)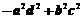
6.设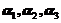 是三维向量,则对任意的常数
是三维向量,则对任意的常数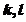 ,向量
,向量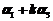 ,
,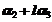 线性无关是向量
线性无关是向量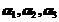 线性无关的( )
线性无关的( )
(A)必要而非充分条件 (B)充分而非必要条件 (C)充分必要条件 (D)非充分非必要条件
7.设事件A,B想到独立,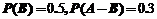 则
则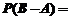 ( )
( )
(A)0.1 (B)0.2 (C)0.3 (D)0.4
8.设连续型随机变量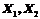 相互独立,且方差均存在,
相互独立,且方差均存在,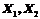 的概率密度分别为
的概率密度分别为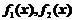 ,随机变量
,随机变量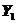 的概率密度为
的概率密度为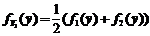 ,随机变量
,随机变量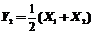 ,则( )
,则( )
(A)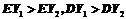 (B)
(B)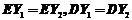
(C)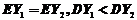 (D)
(D)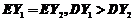
二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
9.曲面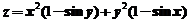 在点
在点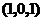 处的切平面方程为 .
处的切平面方程为 .
10.设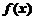 为周期为4的可导奇函数,且
为周期为4的可导奇函数,且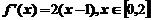 ,则
,则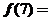 .
.
11.微分方程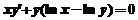 满足
满足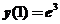 的解为 .
的解为 .
12.设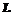 是柱面
是柱面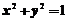 和平面
和平面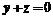 的交线,从
的交线,从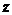 轴正方向往负方向看是逆时针方向,则曲线积分
轴正方向往负方向看是逆时针方向,则曲线积分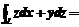 .
.
13.设二次型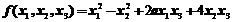 的负惯性指数是1,则
的负惯性指数是1,则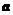 的取值范围是 .
的取值范围是 .
14.设总体X的概率密度为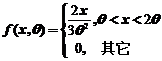 ,其中
,其中 是未知参数,
是未知参数,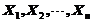 是来自总体的简单样本,若
是来自总体的简单样本,若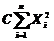 是
是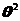 的无偏估计,则常数
的无偏估计,则常数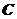 = .
= .
三、解答题
15.(本题满分10分)
求极限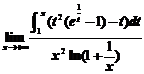 .
.
16.(本题满分10分)
设函数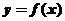 由方程
由方程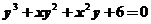 确定,求
确定,求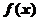 的极值.
的极值.
17.(本题满分10分)
设函数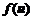 具有二阶连续导数,
具有二阶连续导数,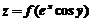 满足
满足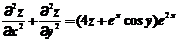 .若
.若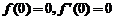 ,求
,求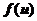 的表达式.
的表达式.
18.(本题满分10分)
设曲面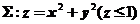 的上侧,计算曲面积分:
的上侧,计算曲面积分: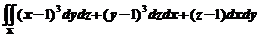
(1) 证明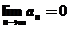 ;
;
(2) 证明级数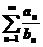 收敛.
收敛.
19.(本题满分10分)
设数列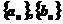 满足
满足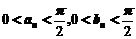 ,
,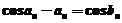 且级数
且级数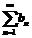 收敛.
收敛.
20.(本题满分11分)
设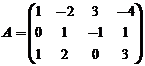 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
(3) 求方程组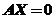 的一个基础解系;
的一个基础解系;
(4) 求满足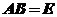 的所有矩阵.
的所有矩阵.
21.(本题满分11分)
证明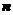 阶矩阵
阶矩阵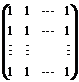 与
与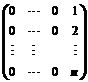 相似.
相似.
22.(本题满分11分)
设随机变量X的分布为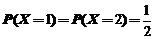 ,在给定
,在给定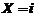 的条件下,随机变量
的条件下,随机变量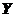 服从均匀分布
服从均匀分布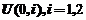 .
.
(5) 求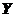 的分布函数;
的分布函数;
(6) 求期望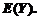
23.(本题满分11分)
设总体X的分布函数为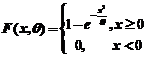 ,其中
,其中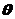 为未知的大于零的参数,
为未知的大于零的参数,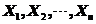 是来自总体的简单随机样本,
是来自总体的简单随机样本,
(1)求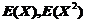 ;(2)求
;(2)求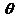 的极大似然估计量.
的极大似然估计量.
(3)是否存在常数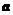 ,使得对任意的
,使得对任意的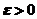 ,都有
,都有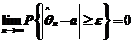 .
.
2013年考研数学一解析
1.【详解】对于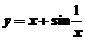 ,可知
,可知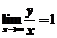 且
且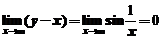 ,所以有斜渐近线
,所以有斜渐近线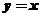
应该选(C)
2.【详解1】如果对曲线在区间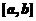 上凹凸的定义比较熟悉的话,可以直接做出判断.如果对区间上任意两点
上凹凸的定义比较熟悉的话,可以直接做出判断.如果对区间上任意两点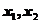 及常数
及常数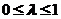 ,恒有
,恒有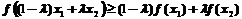 ,则曲线是凸的.显然此题中
,则曲线是凸的.显然此题中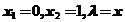 ,则
,则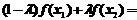
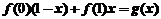 ,
,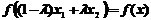 ,
,
故当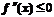 时,曲线是凸的,即
时,曲线是凸的,即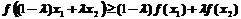 ,也就是
,也就是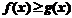 ,应该选(C)
,应该选(C)
【详解2】如果对曲线在区间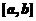 上凹凸的定义不熟悉的话,可令
上凹凸的定义不熟悉的话,可令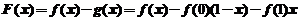 ,则
,则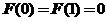 ,且
,且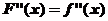 ,故当
,故当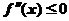 时,曲线是凸的,从而
时,曲线是凸的,从而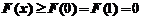 ,即
,即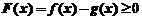 ,也就是
,也就是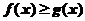 ,应该选(C)
,应该选(C)
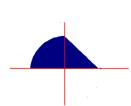 3.【详解】积分区域如图所示。如果换成直角坐标则应该是:
3.【详解】积分区域如图所示。如果换成直角坐标则应该是:
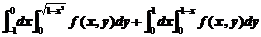 ,(A),(B)两个选择项都不正确;
,(A),(B)两个选择项都不正确;
如果换成极坐标则为:
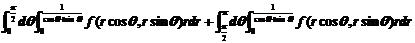 .应选(D)
.应选(D)
4.【详解】注意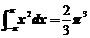 ,
,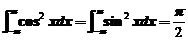 ,
,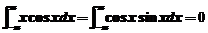 ,
,
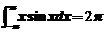 ,所以
,所以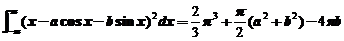
所以就相当于求函数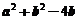 的极小值点,显然可知当
的极小值点,显然可知当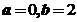 时取得最小值,所以应该选(A).
时取得最小值,所以应该选(A).
5.【详解】
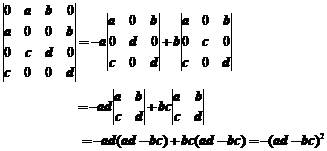
应该选(B).
6.【详解】若向量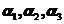 线性无关,则(
线性无关,则(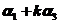 ,
,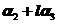 )
)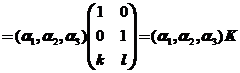 ,对任意的常数
,对任意的常数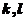 ,矩阵
,矩阵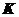 的秩都等于2,所以向量
的秩都等于2,所以向量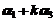 ,
,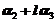 一定线性无关.而当
一定线性无关.而当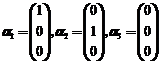 时,对任意的常数
时,对任意的常数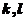 ,向量
,向量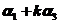 ,
,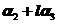 线性无关,但
线性无关,但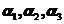 线性相关;故选择(A).
线性相关;故选择(A).
7.【详解】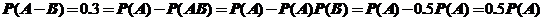 .
.
所以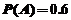 ,
,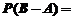
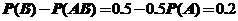 .故选择(B).
.故选择(B).
8.【详解】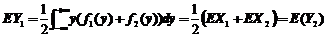 ,
,
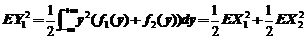 ,
,
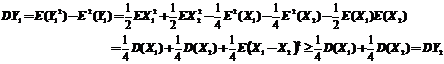
故应该选择(D).
9.【详解】曲面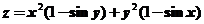 在点
在点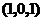 处的法向量为
处的法向量为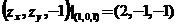 ,所以切平面方程为
,所以切平面方程为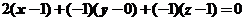 ,即
,即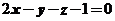 .
.
10.【详解】当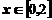 时,
时,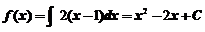 ,由
,由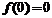 可知
可知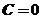 ,即
,即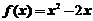 ;
;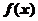 为周期为4奇函数,故
为周期为4奇函数,故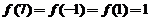 .
.
11.【详解】方程的标准形式为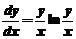 ,这是一个齐次型方程,设
,这是一个齐次型方程,设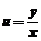 ,得到通解为
,得到通解为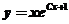 ,将初始条件
,将初始条件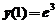 代入可得特解为
代入可得特解为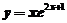 .
.
12.【详解】由斯托克斯公式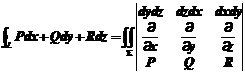 可知
可知
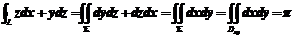 .其中
.其中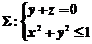 取上侧,
取上侧,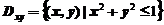 .
.
13.【详解】由配方法可知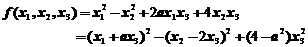
由于负惯性指数为1,故必须要求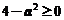 ,所以
,所以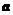 的取值范围是
的取值范围是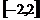 .
.
14.【详解】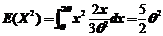 ,所以
,所以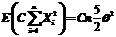 ,由于
,由于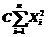 是
是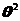 的无偏估计,故
的无偏估计,故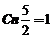 ,
,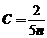 .
.
15.【分析】.先用等价无穷小代换简化分母,然后利用洛必达法则求未定型极限.
【详解】
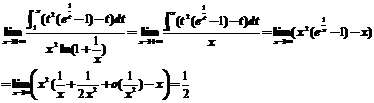
16.【详解】
解:在方程两边同时对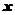 求导一次,得到
求导一次,得到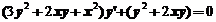 , (1)
, (1)
即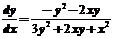 ,令
,令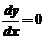 及
及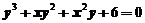 ,得到函数唯一驻点
,得到函数唯一驻点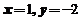 .
.
在(1)式两边同时对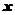 求导一次,得到
求导一次,得到 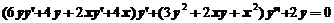
把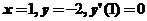 代入,得到
代入,得到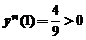 ,所以函数
,所以函数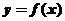 在
在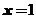 处取得极小值
处取得极小值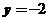 .
.
17.【详解】
设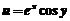 ,则
,则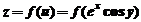 ,
,
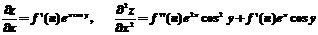 ;
;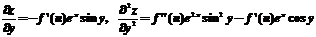
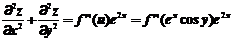 ,由条件
,由条件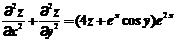 ,可知
,可知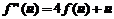
这是一个二阶常用系数线性非齐次方程.对应齐次方程的通解为: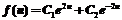 其中
其中 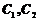 为任意常数. 对应非齐次方程特解可求得为
为任意常数. 对应非齐次方程特解可求得为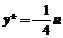 .故非齐次方程通解为
.故非齐次方程通解为 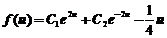 .将初始条件
.将初始条件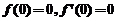 代入,可得
代入,可得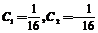 .所以
.所以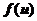 的表达式为
的表达式为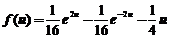 .
.
18.【详解】
设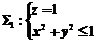 取下侧,记由
取下侧,记由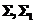 所围立体为
所围立体为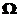 ,则高斯公式可得
,则高斯公式可得
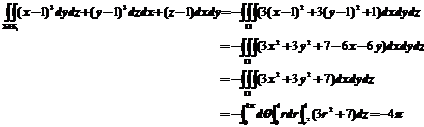
在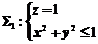 取下侧上,
取下侧上,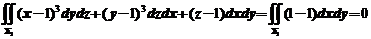 ,
,
所以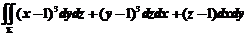 =
=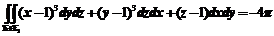
19.【详解】
(1)证明:由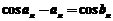 ,及
,及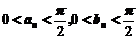 可得
可得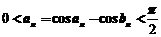 ,
,
所以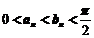 ,由于级数
,由于级数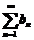 收敛,所以级数
收敛,所以级数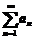 也收敛,由收敛的必要条件可得
也收敛,由收敛的必要条件可得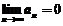 .
.
(2)证明:由于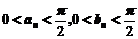 ,所以
,所以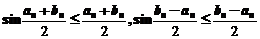
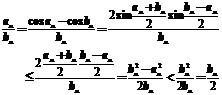
由于级数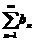 收敛,由正项级数的比较审敛法可知级数
收敛,由正项级数的比较审敛法可知级数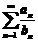 收敛.
收敛.
20.【详解】(1)对系数矩阵A进行初等行变换如下:
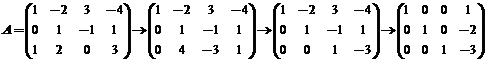 ,
,
得到方程组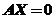 同解方程组
同解方程组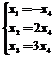 ,得到
,得到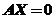 的一个基础解系
的一个基础解系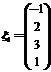 .
.
显然B矩阵是一个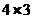 矩阵,设
矩阵,设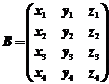
对矩阵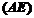 进行进行初等行变换如下:
进行进行初等行变换如下:
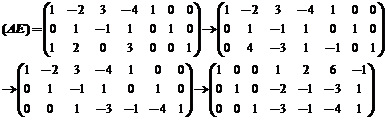
由方程组可得矩阵B对应的三列分别为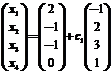 ,
,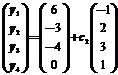 ,
,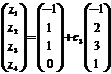 ,
,
即满足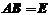 的所有矩阵为
的所有矩阵为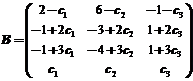 ,其中
,其中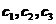 为任意常数.
为任意常数.
21.【详解】证明:设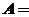
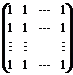 ,
,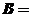
 .
.
分别求两个矩阵的特征值和特征向量如下:
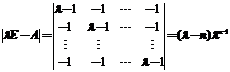 , 所以A的
, 所以A的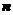 个特征值为
个特征值为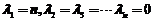 ;
;
而且A是实对称矩阵,所以一定可以对角化.且 ;
;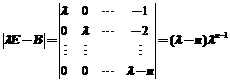
所以B的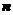 个特征值也为
个特征值也为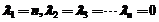 ;对于
;对于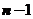 重特征值
重特征值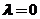 ,由于矩阵
,由于矩阵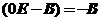 的秩显然为1,所以矩阵B对应
的秩显然为1,所以矩阵B对应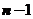 重特征值
重特征值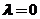 的特征向量应该有
的特征向量应该有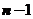 个线性无关,进一步矩阵B存在
个线性无关,进一步矩阵B存在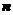 个线性无关的特征向量,即矩阵B一定可以对角化,且
个线性无关的特征向量,即矩阵B一定可以对角化,且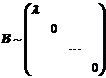 ,从而可知
,从而可知 阶矩阵
阶矩阵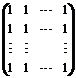 与
与 相似.
相似.
22.【详解】(1)分布函数
当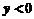 时,
时,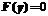 ;
;
当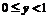 时,
时,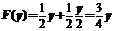 ;
;
当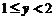 时,
时,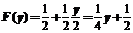 ;
;
当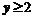 时,
时,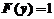 .
.
所以分布函数为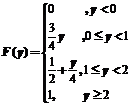
(2)概率密度函数为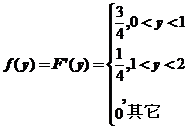 ,
, 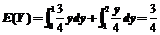 .
.
23.【详解】(1)先求出总体X的概率密度函数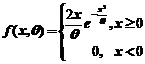 ,
,
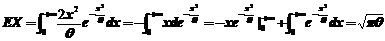 ;
;

(2)极大似然函数为:
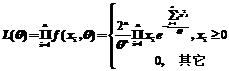
当所有的观测值都大于零时,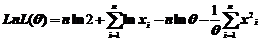 ,令
,令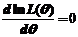 ,
,
得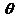 的极大似然估计量为
的极大似然估计量为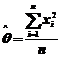 ;
;
(3)因为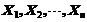 独立同分布,显然对应的
独立同分布,显然对应的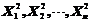 也独立同分布,又有(1)个可知
也独立同分布,又有(1)个可知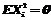 ,由辛钦大数定律,可得
,由辛钦大数定律,可得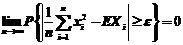 ,由前两问可知,
,由前两问可知,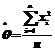 ,
,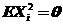 ,所以存在常数
,所以存在常数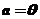 ,使得对任意的
,使得对任意的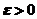 ,都有
,都有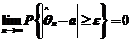 .
.