|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
所以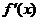 为单调增函数. 又因为 为单调增函数. 又因为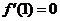 ,所以有 ,所以有
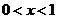 时 时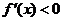 ; ;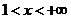 时 时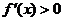 , ,
所以利用函数单调性可知,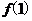 为 为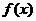 的最小值,即 的最小值,即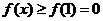
所以有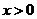 时, 时,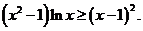
证法2:先对要证的不等式作适当变形,当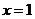 时,原不等式显然成立; 时,原不等式显然成立;
当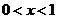 时,原不等式等价于 时,原不等式等价于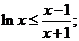
当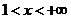 时,原不等式等价于 时,原不等式等价于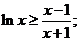
令 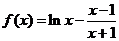
则 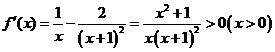
又因为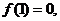 利用函数单调性可知 利用函数单调性可知
当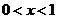 时, 时,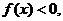 即 即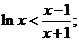 当 当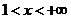 时, 时,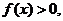 即 即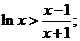
综上所述,当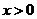 时, 时,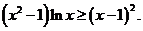
七【详解】建立坐标轴如图所示,
解法1:将抓起污泥的抓斗提升至井口需做功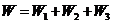 ,其中 ,其中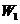 是克服抓斗自重所作的功; 是克服抓斗自重所作的功;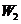 是克服缆绳重力作的功; 是克服缆绳重力作的功;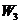 为提出污泥所作的功. 由题意知 为提出污泥所作的功. 由题意知
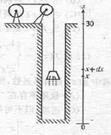 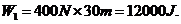
将抓斗由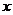 处提升到 处提升到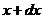 处,克服缆绳重力所作的功为 处,克服缆绳重力所作的功为
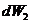 = 缆绳每米重×缆绳长×提升高度 = 缆绳每米重×缆绳长×提升高度
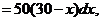
从而 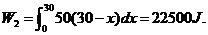
在时间间隔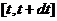 内提升污泥需做功为 内提升污泥需做功为
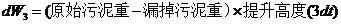
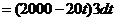
将污泥从井底提升至井口共需时间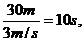
所以 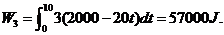
因此,共需做功
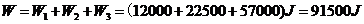
解法2:将抓起污泥的抓斗提升至井口需做功记为 ,当抓斗运动到 ,当抓斗运动到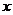 处时,作用力 处时,作用力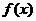 包括抓斗的自重 包括抓斗的自重 , 缆绳的重力 , 缆绳的重力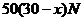 , 污泥的重力 , 污泥的重力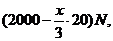
即 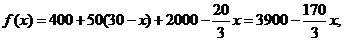
于是 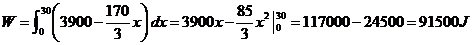
八【分析】先写出切平面方程,然后求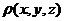 ,最后将曲面积分化成二重积分. ,最后将曲面积分化成二重积分.
【详解】点 , ,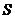 在点 在点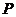 处的法向量为 处的法向量为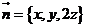 ,设 ,设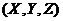 为 为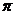 上任意一点,则 上任意一点,则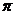 的方程为 的方程为
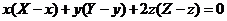 ,化简得 ,化简得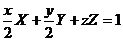
由点到平面的公式,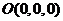 到 到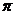 的距离 的距离
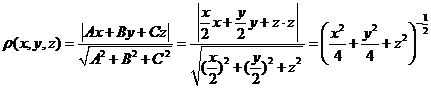
从而 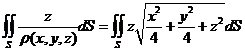
用投影法计算此第一类曲面积分,将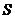 投影到 投影到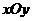 平面,其投影域为 平面,其投影域为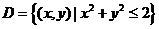
由曲面方程知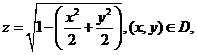 于是 于是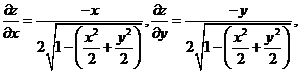
因此 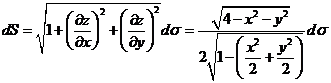
故有 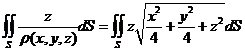
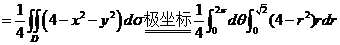 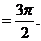
九【详解】(1) 因为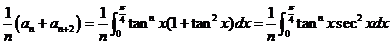
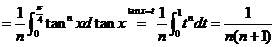
又由部分和数列
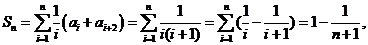
有 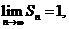
因此 
(2) 先估计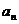 的值,因为 的值,因为
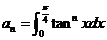 ,令 ,令 ,则 ,则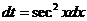 ,即 ,即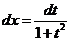
所以 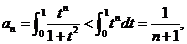
所以 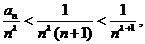
由于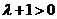 ,所以 ,所以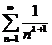 收敛,从而 收敛,从而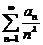 也收敛. 也收敛.
十【详解】根据题设,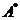 有一个特征值 有一个特征值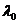 ,属于 ,属于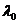 的一个特征向量为 的一个特征向量为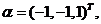 根据特征值和特征向量的概念,有 根据特征值和特征向量的概念,有 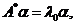
把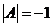 代入 代入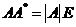 中,得 中,得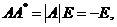 则 则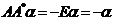 . 把 . 把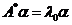 代入,于是 代入,于是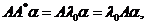 即 即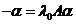
也即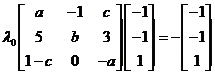 , ,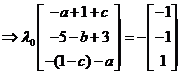
常数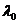 乘以矩阵 乘以矩阵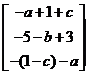 ,需用 ,需用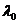 乘以矩阵的每一个元素 乘以矩阵的每一个元素
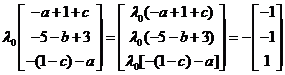
矩阵相等,则矩阵的对应元素都相同,可得
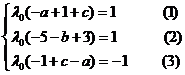
因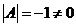 , , 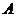 的特征值 的特征值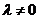 , ,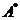 的特征值 的特征值 ,故 ,故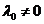
由(1),(3)两式得
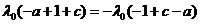 , ,
两边同除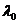 ,得 ,得 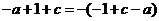
整理得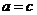 ,代入(1)中,得 ,代入(1)中,得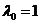 . 再把 . 再把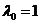 代入(2)中得 代入(2)中得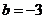
又由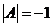 , ,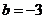 以及 以及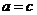 ,有 ,有
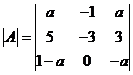 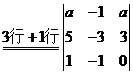 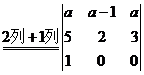
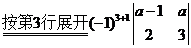 (其中 (其中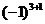 的指数3,1分别是1的行数和列数) 的指数3,1分别是1的行数和列数)
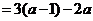 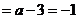
故 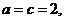 因此 因此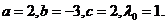
十一【详解】
“必要性”. 设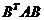 为正定矩阵,则由定义知,对任意的实 为正定矩阵,则由定义知,对任意的实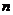 维列向量 维列向量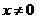 ,有 ,有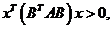 即 即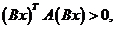 于是, 于是,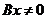 ,即对任意的实 ,即对任意的实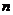 维列向量 维列向量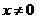 ,都有 ,都有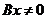 . (若 . (若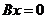 ,则 ,则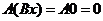 矛盾). 因此, 矛盾). 因此,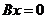 只有零解,故有 只有零解,故有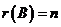 ( (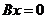 有唯一零解的充要条件是 有唯一零解的充要条件是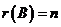 ). ).
“充分性”. 因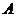 为 为 阶实对称矩阵,则 阶实对称矩阵,则 ,故 ,故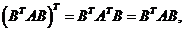 根据实对称矩阵的定义知 根据实对称矩阵的定义知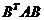 也为实对称矩阵. 若 也为实对称矩阵. 若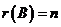 ,则线性方程组 ,则线性方程组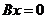 只有零解,从而对任意的实 只有零解,从而对任意的实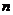 维列向量 维列向量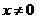 ,有 ,有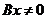 . 又 . 又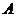 为正定矩阵,所以对于 为正定矩阵,所以对于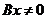 有 有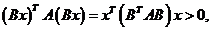 故 故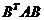 为正定矩阵(对任意的实 为正定矩阵(对任意的实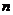 维列向量 维列向量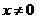 ,有 ,有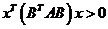 ). ).
十二【详解】离散型随机变量边缘分布律的定义:
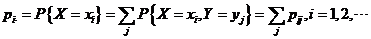
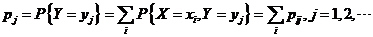
(通俗点说就是在求关于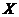 的边缘分布时,就把对应 的边缘分布时,就把对应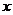 的所有 的所有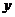 都加起来,同理求关于 都加起来,同理求关于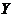 的边缘分布时,就把对应 的边缘分布时,就把对应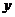 的所有 的所有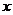 都加起来) 都加起来)
故 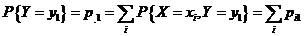 即 即
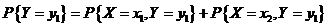
而由表知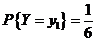 , ,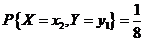 ,所以 ,所以

又根据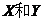 相互独立,则有: 相互独立,则有:
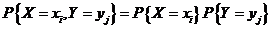 即 即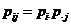
因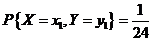 , ,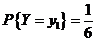 ,而 ,而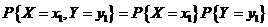
所以
再由边缘分布的定义有
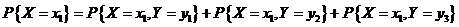
所以 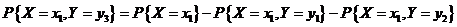
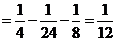
又由独立性知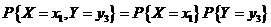
所以 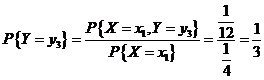
由边缘分布定义有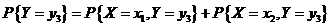
所以 
再由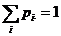 ,所以 ,所以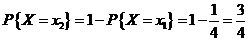
而 
故 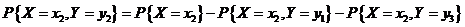
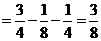
又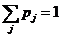 ,所以 ,所以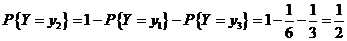
所以有:
十三【详解】矩估计的实质在于用样本矩来估计相应的总体矩,此题中被估参数只有一个,故只需要用样本矩(样本均值)来估计总体的一阶原点矩(期望)
(1) 矩估计:由期望的定义:
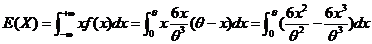
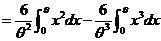 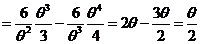
样本均值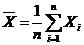 ,用样本均值估计期望有 ,用样本均值估计期望有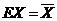 , ,
即 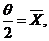 解得θ的矩估计量 解得θ的矩估计量 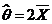
(2) 由随机变量方差的性质: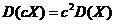 ,所以 ,所以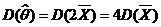
又由独立随机变量方差的性质:若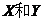 独立,则 独立,则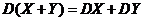
因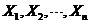 是取自总体 是取自总体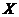 的简单随机样本,所以 的简单随机样本,所以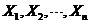 独立且 独立且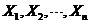 与 与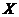 服从同一分布,即 服从同一分布,即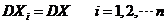
而 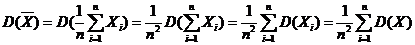
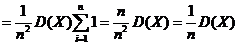
方差的定义: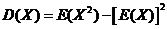 ,所以求方差只需要求出 ,所以求方差只需要求出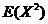 和 和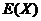
根据二阶原点矩的定义: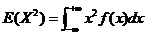
故 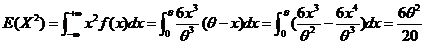
而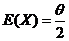 ,所以 ,所以
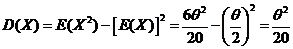
因此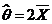 的方差为 的方差为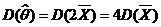 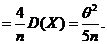
|