微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
【考点】常用分布的数字特征
【详解】本题涉及到的主要知识点:
泊松分布:设随机变量X的分布律为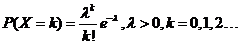 ,则称随机变量X服从参数为λ的泊松分布,记为X~π(λ)或者P(λ)。
,则称随机变量X服从参数为λ的泊松分布,记为X~π(λ)或者P(λ)。
泊松分布的数字特征:E(X)=λ,D(X)=λ。
公式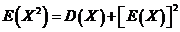
在本题中,
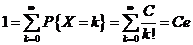 (利用
(利用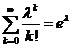 ),所以
),所以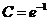
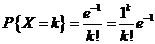 即
即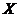 服从参数为1的泊松分布.
服从参数为1的泊松分布.
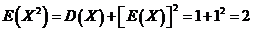
三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(15) (本题满分10分)
求微分方程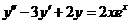 的通解
的通解
【考点】二阶常系数非齐次线性微分方程
【详解】本题涉及到的主要知识点:
二阶常系数其次线性方程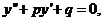 其中p,q为常数,
其中p,q为常数,
特征方程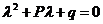
特征方程根的三种不同情形对应方程通解的三种形式
(1)当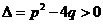 ,特征方程有两个不同的实数
,特征方程有两个不同的实数
则方程的通解为 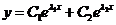
(2)当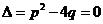 ,特征方程有二重根
,特征方程有二重根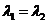 。
。
则方程的通解为 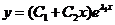
(3)当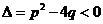 ,特征方程有共轭复根
,特征方程有共轭复根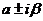 ,
,
则方程的通解为 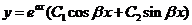 。
。
在本题中,
先求方程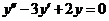 的通解
的通解
由特征方程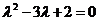 解得特征根
解得特征根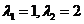
所以方程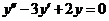 的通解为
的通解为
下求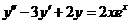 的特解:设特解为
的特解:设特解为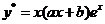 ,则
,则
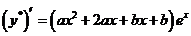 ,
,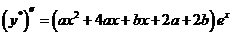
代入原方程,解得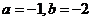 ,故特解为
,故特解为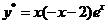
故方程的通解为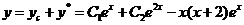
(16) (本题满分10分)
求函数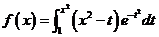 的单调区间与极值.
的单调区间与极值.
【考点】函数单调性的判别
【详解】本题涉及到的主要知识点:
函数单调性的判断:求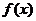 的单调性区间,就是求
的单调性区间,就是求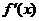 的正负号区间。增减或减增区间的分界点就是极值点。
的正负号区间。增减或减增区间的分界点就是极值点。
在本题中,
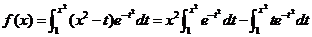
所以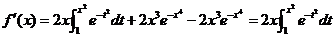
令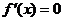 ,则
,则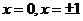 ;
;
因为当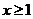 时,
时,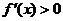 ,
,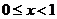 时,
时,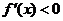 ,
,
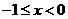 时,
时,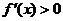 ,
, 时,
时,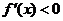 ;
;
所以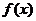 的单调递减区间为
的单调递减区间为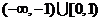 ;
;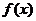 的单调递增区间为
的单调递增区间为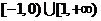
所以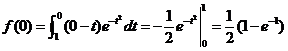 是极大值.
是极大值.
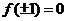 为极小值.
为极小值.
(17) (本题满分10分)
(I) 比较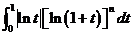 与
与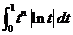
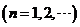 的大小,说明理由;
的大小,说明理由;
(II) 记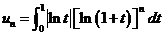
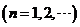 ,求极限
,求极限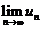 .
.
【考点】定积分的性质,夹逼准则
【详解】本题涉及到的主要知识点:
夹逼定理:设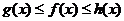 ,若
,若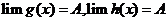 ,则
,则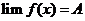 。
。
在本题中,
当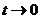 时,
时,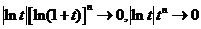 ,所以
,所以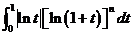 与
与
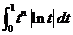 均为定积分,故
均为定积分,故
(I)当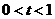 时
时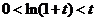 ,
,
故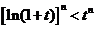 ,所以
,所以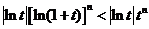
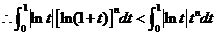
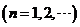
(II)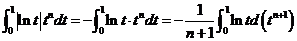
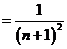
故由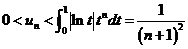 ,
,
根据夹逼定理得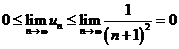
故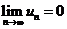 .
.
(18) (本题满分10分)
求幂级数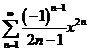 的收敛域及和函数.
的收敛域及和函数.
【考点】幂级数的收敛域及和函数
【详解】本题涉及到的主要知识点:
幂级数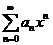 的收敛域的定义及求法,分三种情况:
的收敛域的定义及求法,分三种情况:
(1)收敛域为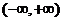 ,亦即
,亦即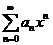 对每一个x皆收敛,此时收敛半径R=+∞
对每一个x皆收敛,此时收敛半径R=+∞
(2)收敛域仅为原点,除原点外幂级数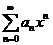 皆发散,称收敛半径R=0.
皆发散,称收敛半径R=0.
(3)收敛半径为R,(0<R<+∞).
如果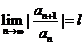 (包括+∞)或
(包括+∞)或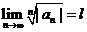 (包括+∞),则收敛半径R=
(包括+∞),则收敛半径R=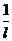 。
。
若上述两极限不成立,则要用其他方法求收敛半径。
在本题中,
令
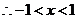 时级数收敛.
时级数收敛.
当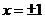 时,
时,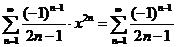 ,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为
,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为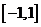 .
.
设 
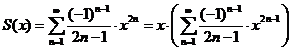
令 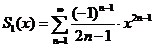
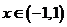 ,
,
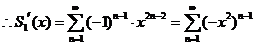
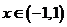 ,
,

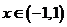 ,
,
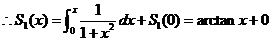 ,
,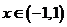 .
.
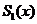 在
在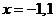 上是连续的,所以
上是连续的,所以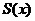 在收敛域
在收敛域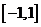 上是连续的.
上是连续的.
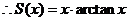 .
. 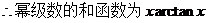 ,
,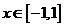 .
.
(19) (本题满分10分)
设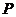 为椭球面
为椭球面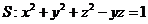 上的动点,若
上的动点,若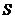 在点
在点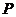 处的切平面为
处的切平面为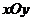 面垂直,求点
面垂直,求点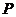 的轨迹
的轨迹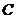 ,并计算曲面积分
,并计算曲面积分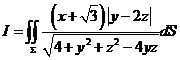 ,其中
,其中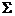 是椭球面
是椭球面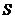 位于曲线
位于曲线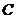 上方的部分.
上方的部分.
【考点】曲面的切平面和法线,计算第一类曲面积分的方法
【详解】本题涉及到的主要知识点:
这是一道综合题,主要涉及第一类曲面积分的计算方法,以及平面的法线和切平面等一些概念。基本计算公式:
设曲面S的方程z=z(x,y), (x,y)∈D。 z(x,y)在D上有连续偏导数,f(x,y,z)在S上连续,则
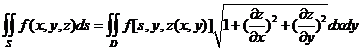
这样把第一类曲面积分化为二重积分进行计算。
在本题中,
令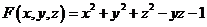
故动点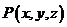 的切平面的法向量为
的切平面的法向量为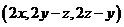 ;
;
由切平面垂直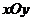 ,故所求曲线
,故所求曲线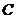 的方程为:
的方程为: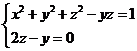
由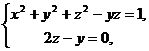 消去
消去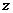 ,立马可得投影柱面
,立马可得投影柱面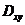 :
: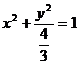 ,
,
由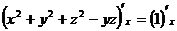 ,得
,得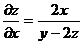 ,同理得,
,同理得, 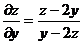
因而可得 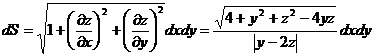 ,
,
所以, 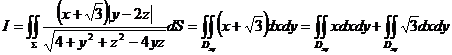
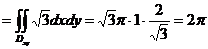 .
.
(20) (本题满分11分)
设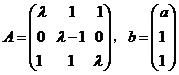
已知线性方程组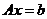 存在2个不同的解
存在2个不同的解
(I) 求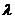 ,
,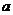 ;
;
(II) 求方程组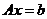 的通解.
的通解.
【考点】非齐次线性方程组的解;非齐次线性方程组的通解
【详解】本题涉及到的主要知识点:
非齐次线性方程组有解的充分必要条件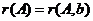 。
。
非齐次线性方程组解的结构式齐次线性方程组的通解加上特解。
在本题中,
方法一:(I)已知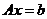 有2个不同的解
有2个不同的解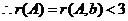 ,对增广矩阵进行初等行变换,得
,对增广矩阵进行初等行变换,得

当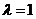 时,
时,
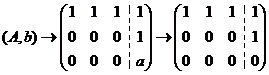
此时,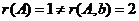 ,
,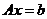 无解,所以
无解,所以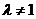 。
。
当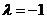 ,
,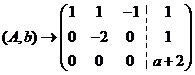
由于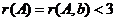 ,所以
,所以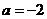 。因此,
。因此,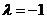 ,
,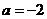 。
。
方法二:(I)已知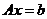 有2个不同的解
有2个不同的解
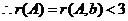
又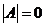 ,即
,即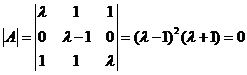 ,知
,知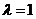 或-1。
或-1。
当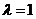 时,
时,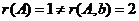 ,此时,
,此时,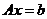 无解,
无解,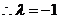 。代入由
。代入由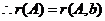 得
得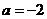 。 &nbs
。 &nbs