微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2015年考研数学一真题
一、选择题 1—8小题.每小题4分,共32分.
 1.设函数
1.设函数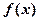 在
在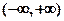 上连续,其二阶导数
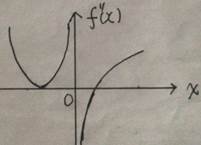
上连续,其二阶导数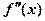 的图形如右图所示,则曲线
的图形如右图所示,则曲线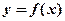 在
在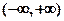 的拐点个数为
的拐点个数为
(A)0 (B)1 (C)2 (D)3
【详解】对于连续函数的曲线而言,拐点处的二阶导数等于零或者不存在.从图上可以看出有两个二阶导数等于零的点,以及一个二阶导数不存在的点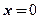 .但对于这三个点,左边的二阶导数等于零的点的两侧二阶导数都是正的,所以对应的点不是拐点.而另外两个点的两侧二阶导数是异号的,对应的点才是拐点,所以应该选(C)
.但对于这三个点,左边的二阶导数等于零的点的两侧二阶导数都是正的,所以对应的点不是拐点.而另外两个点的两侧二阶导数是异号的,对应的点才是拐点,所以应该选(C)
2.设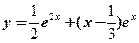 是二阶常系数非齐次线性微分方程
是二阶常系数非齐次线性微分方程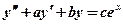 的一个特解,则
的一个特解,则
(A)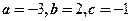 (B)
(B)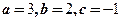
(C)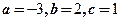 (D)
(D)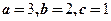
【详解】线性微分方程的特征方程为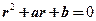 ,由特解可知
,由特解可知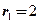 一定是特征方程的一个实根.如果
一定是特征方程的一个实根.如果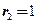 不是特征方程的实根,则对应于
不是特征方程的实根,则对应于 的特解的形式应该为
的特解的形式应该为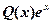 ,其中
,其中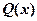 应该是一个零次多项式,即常数,与条件不符,所以
应该是一个零次多项式,即常数,与条件不符,所以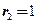 也是特征方程的另外一个实根,这样由韦达定理可得
也是特征方程的另外一个实根,这样由韦达定理可得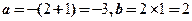 ,同时
,同时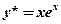 是原来方程的一个解,代入可得
是原来方程的一个解,代入可得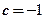 应该选(A)
应该选(A)
3.若级数 条件收敛,则
条件收敛,则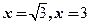 依次为级数
依次为级数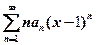 的
的
(A)收敛点,收敛点 (B)收敛点,发散点
(C)发散点,收敛点 (D)发散点,发散点
【详解】注意条件级数 条件收敛等价于幂级数
条件收敛等价于幂级数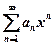 在
在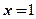 处条件收敛,也就是这个幂级数的收敛为
处条件收敛,也就是这个幂级数的收敛为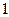 ,即
,即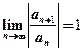 ,所以
,所以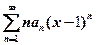 的收敛半径
的收敛半径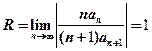 ,绝对收敛域为
,绝对收敛域为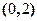 ,显然
,显然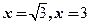 依次为收敛点、发散点,应该选(B)
依次为收敛点、发散点,应该选(B)
4.设D是第一象限中由曲线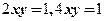 与直线
与直线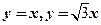 所围成的平面区域,函数
所围成的平面区域,函数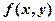 在D上连续,则
在D上连续,则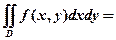 ( )
( )
(A)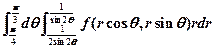 (B)
(B)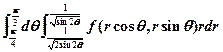
 (C)
(C)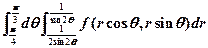 (D)
(D)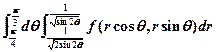
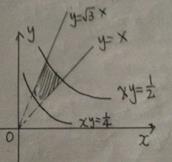
【详解】积分区域如图所示,化成极坐标方程:
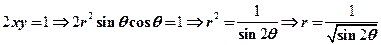
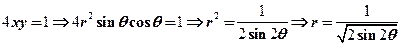
也就是D: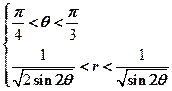
所以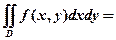
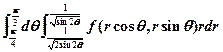 ,所以应该选(B).
,所以应该选(B).
5.设矩阵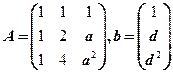 ,若集合
,若集合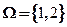 ,则线性方程组
,则线性方程组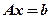 有无穷多解的充分必要条件是
有无穷多解的充分必要条件是
(A)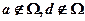 (B)
(B)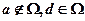
(C)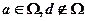 (D)
(D)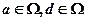
【详解】对线性方程组的增广矩阵进行初等行变换:
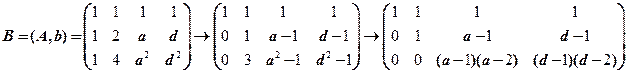
方程组无穷解的充分必要条件是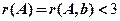 ,也就是
,也就是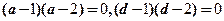 同时成立,当然应该选(D).
同时成立,当然应该选(D).
6.设二次型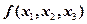 在正交变换
在正交变换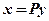 下的标准形为
下的标准形为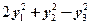 ,其中
,其中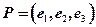 ,若
,若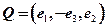 ,则
,则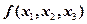 在
在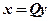 下的标准形为
下的标准形为
(A)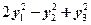 (B)
(B)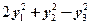
(C)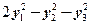 (D)
(D) 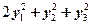
【详解】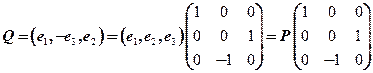 ,
,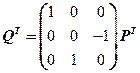
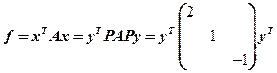
所以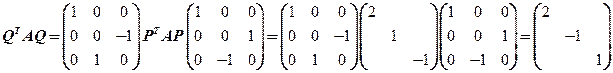
故选择(A).
7.若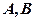 为任意两个随机事件,则( )
为任意两个随机事件,则( )
(A)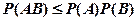 (B)
(B)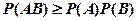
(C)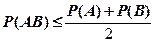 (D)
(D)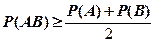
【详解】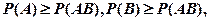 所以
所以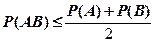 故选择(C).
故选择(C).
8.设随机变量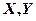 不相关,且
不相关,且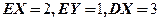 ,则
,则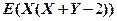
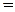 ( )
( )
(A)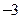 (B)
(B)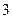 (C)
(C)  (D)
(D)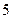
【详解】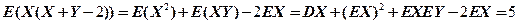
故应该选择(D).
二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
9.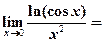
【详解】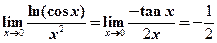 .
.
10.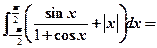 .
.
【详解】只要注意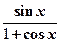 为奇函数,在对称区间上积分为零,
为奇函数,在对称区间上积分为零,
所以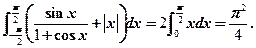
11.若函数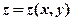 是由方程
是由方程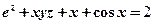 确定,则
确定,则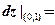 .
.
【详解】设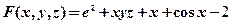 ,则
,则
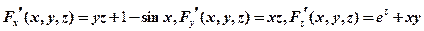
且当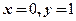 时,
时,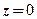 ,所以
,所以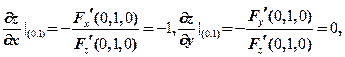
也就得到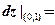
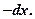
12.设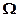 是由平面
是由平面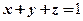 和三个坐标面围成的空间区域,则
和三个坐标面围成的空间区域,则
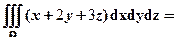 .
.
【详解】注意在积分区域内,三个变量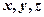 具有轮换对称性,也就是
具有轮换对称性,也就是

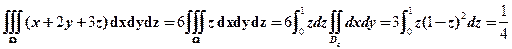
13.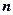 阶行列式
阶行列式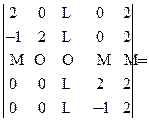 .
.
【详解】按照第一行展开,得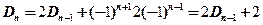 ,有
,有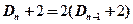
由于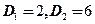 ,得
,得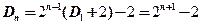 .
.
14.设二维随机变量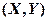 服从正态分布
服从正态分布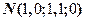 ,则
,则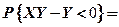 .
.
【详解】由于相关系数等于零,所以X,Y都服从正态分布,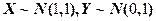 ,且相互独立.
,且相互独立.
则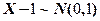 .
.
三、解答题
15.(本题满分10分)设函数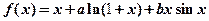 ,
,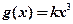 在
在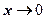 时为等价无穷小,求常数
时为等价无穷小,求常数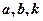 的取值.
的取值.
【详解】当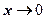 时,把函数
时,把函数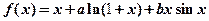 展开到三阶的马克劳林公式,得
展开到三阶的马克劳林公式,得
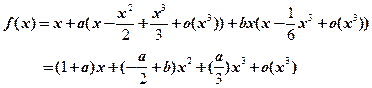
由于当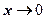 时,
时,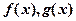 是等价无穷小,则有
是等价无穷小,则有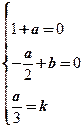 ,
,
解得,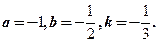
16.(本题满分10分)
设函数 在定义域
在定义域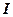 上的导数大于零,若对任意的
上的导数大于零,若对任意的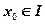 ,曲线
,曲线 在点
在点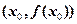 处的切线与直线
处的切线与直线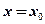 及
及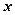 轴所围成区域的面积恒为4,且
轴所围成区域的面积恒为4,且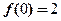 ,求
,求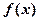 的表达式.
的表达式.
【详解】 在点
在点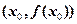 处的切线方程为
处的切线方程为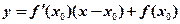
令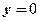 ,得
,得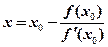
曲线 在点
在点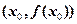 处的切线与直线
处的切线与直线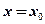 及
及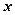 轴所围成区域的面积为
轴所围成区域的面积为
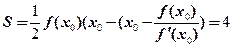
整理,得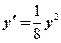 ,解方程,得
,解方程,得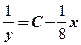 ,由于
,由于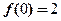 ,得
,得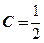
所求曲线方程为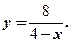
17.(本题满分10分)
设函数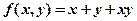 ,曲线
,曲线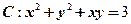 ,求
,求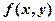 在曲线
在曲线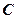 上的最大方向导数.
上的最大方向导数.
【详解】显然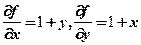 .
.
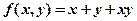 在
在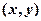 处的梯度
处的梯度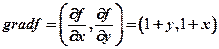
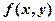 在
在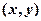 处的最大方向导数的方向就是梯度方向,最大值为梯度的模
处的最大方向导数的方向就是梯度方向,最大值为梯度的模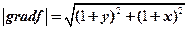
所以此题转化为求函数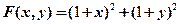 在条件
在条件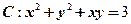 下的条件极值.用拉格朗日乘子法求解如下:
下的条件极值.用拉格朗日乘子法求解如下:
令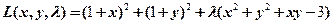
解方程组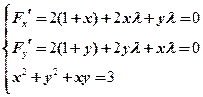 ,得几个可能的极值点
,得几个可能的极值点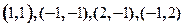 ,
,
进行比较,可得,在点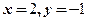 或
或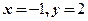 处,方向导数取到最大,为
处,方向导数取到最大,为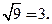
18.(本题满分10分)
(1)设函数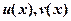 都可导,利用导数定义证明
都可导,利用导数定义证明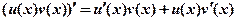 ;
;
(2)设函数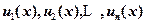 都可导,
都可导,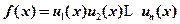 ,写出
,写出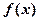 的求导公式.
的求导公式.
【详解】(1)证明:设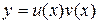

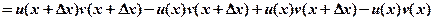
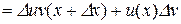
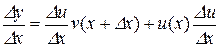
由导数的定义和可导与连续的关系
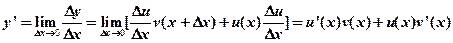
(2)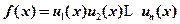
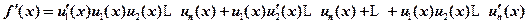
19.(本题满分10分)
已知曲线L的方程为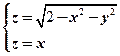 ,起点为
,起点为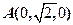 ,终点为
,终点为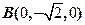 ,计算曲线积分
,计算曲线积分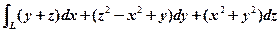 .
.
【详解】曲线L的参数方程为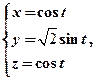
起点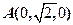 对应
对应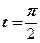 ,终点为
,终点为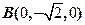 对应
对应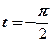 .
.
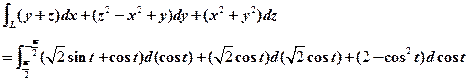
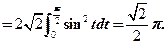
20.(本题满分11分)
设向量组 为向量空间
为向量空间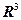 的一组基,
的一组基, .
.
(1)证明:向量组 为向量空间
为向量空间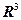 的一组基;
的一组基;
(2)当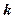 为何值时,存在非零向量
为何值时,存在非零向量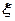 ,使得
,使得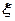 在基
在基 和基
和基 下的坐标相同,并求出所有的非零向量
下的坐标相同,并求出所有的非零向量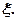
【详解】(1)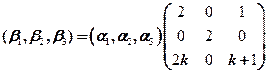 ,
,
因为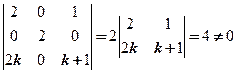 ,且
,且 显然线性无关,所以
显然线性无关,所以 是线性无关的,当然是向量空间
是线性无关的,当然是向量空间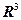 的一组基.
的一组基.
(2)设非零向量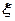 在两组基下的坐标都是
在两组基下的坐标都是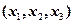 ,则由条件
,则由条件
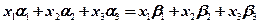
可整理得: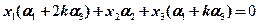 ,所以条件转化为线性方程组
,所以条件转化为线性方程组
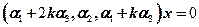 存在非零解.
存在非零解.
从而系数行列式应该等于零,也就是
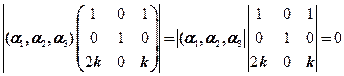
由于 显然线性无关,所以
显然线性无关,所以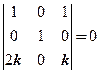 ,也就是
,也就是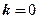 .
.
此时方程组化为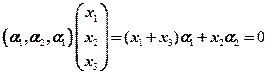 ,
,
由于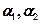 线性无关,所以
线性无关,所以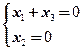 ,通解为
,通解为 ,其中
,其中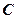 为任意常数.
为任意常数.
所以满足条件的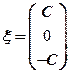 其中
其中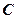 为任意不为零的常数.
为任意不为零的常数.
21.(本题满分11分)
设矩阵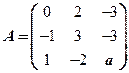 相似于矩阵
相似于矩阵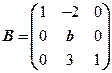 .
.
(1)求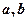 的值;
的值;
(2)求可逆矩阵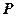 ,使
,使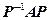 为对角矩阵.
为对角矩阵.
【详解】(1)因为两个矩阵相似,所以有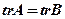 ,
,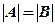 .
.
也就是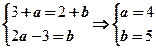 .
.
(2)由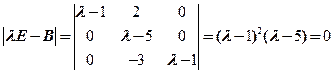 ,得A,B的特征值都为
,得A,B的特征值都为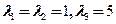
解方程组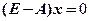 ,得矩阵A的属于特征值
,得矩阵A的属于特征值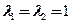 的线性无关的特征向量为
的线性无关的特征向量为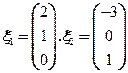 ;
;
解方程组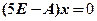 得矩阵A的属于特征值
得矩阵A的属于特征值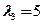 的线性无关的特征向量为
的线性无关的特征向量为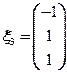
令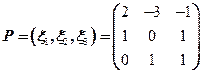 ,则
,则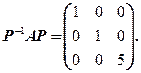
22.(本题满分11分)设随机变量X的概率密度为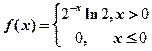
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记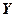 为次数.
为次数.
求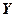 的分布函数;
的分布函数;
(1) 求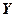 的概率分布;
的概率分布;
(2) 求数学期望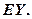
【详解】(1)X进行独立重复的观测,得到观测值大于3的概率为
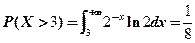
显然Y的可能取值为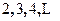
且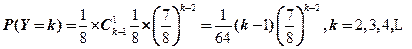
(2)设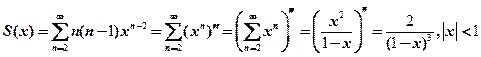
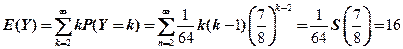
23.(本题满分11分)
设总体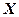 的概率密度为
的概率密度为
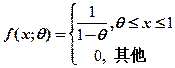
其中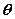 为未知参数,
为未知参数,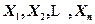 是来自总体的简单样本.
是来自总体的简单样本.
(1)求参数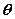 的矩估计量;
的矩估计量;
(2)求参数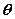 的最大似然估计量.
的最大似然估计量.
【详解】(1)总体的数学期望为
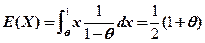
令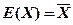 ,解得参数
,解得参数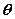 的矩估计量:
的矩估计量: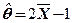 .
.
(2)似然函数为
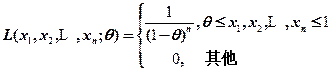
显然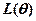 是关于
是关于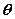 的单调递增函数,为了使似然函数达到最大,只要使
的单调递增函数,为了使似然函数达到最大,只要使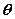 尽可能大就可以,所以
尽可能大就可以,所以
参数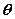 的最大似然估计量为
的最大似然估计量为