1、从某车站以加速度为1/18米/秒2始发的甲列车出发后9分钟,恰好有一列与甲列车同方向,并以50米/秒作匀速运行的乙车通过该车站,则乙车运行多少分钟与甲车距离为最近?_____
A: 9B: 3C: 5D: 6
参考答案: D 本题解释:D。当甲车速度小于乙车时,乙车逐渐缩短与甲车的距离;当甲车速度大于乙车时,两车之间距离拉大;仅当两车速度相同时,两车距离最小。根据Vt=Vo+at,可得50=1/18×9×60+1/18×t,求得t=360秒=6分钟。
2、现在时间为4点13分,此时时针与分针成什么角度?_____
A: 30度B: 45度C: 90度D: 120度
参考答案: B 本题解释:正确答案是B考点钟表问题解析解析1:本题属于钟表问题。把钟面看做圆形,12点为原点。4点13分时针在4和5之间,则120<时针的度数<150,分针的度数=360×13/60=78。可知时针和分针所成的角度x满足120-78<X<150-78。42<X<72,在这个范围内的只有B项45度。故正确答案为B。<p>解析2:把钟面看做圆形,12点为原点。看成追击问题。时针每分钟转的度数为360×1/12×1/60=0.5。分针每分钟转的度数为360×1/60=6。4点13分两针的夹角为120+0.5×13-6×13=48.5≈45。故正确答案为B。
3、
A: AB: BC: CD: D
参考答案: 本题解释:正确答案是B考点行程问题解析 故答案为B。
故答案为B。
4、一堆苹果,每组5个,余3个,每组7个,剩余2个,则这堆苹果的个数最少为_____
A: 31B: 10C: 23D: l
参考答案: C 本题解释:【解析】C。直接代入。
5、在20件产品中,有15件一级品,5件二级品,从中任取3件,其中至少有一件为二级品的概率是多少?_____
A: 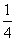 B:
B: 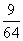 C:
C: 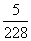 D:
D: 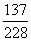
参考答案: D 本题解释:参考答案 题目详解:在20件产品中任取3件:可以有
题目详解:在20件产品中任取3件:可以有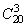 种情况;3件都是一级品的情况为:有
种情况;3件都是一级品的情况为:有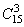 种情况;因此至少有一件为二级品的情况:有
种情况;因此至少有一件为二级品的情况:有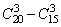 种情况;因此至少有一件为二级品的概率是:
种情况;因此至少有一件为二级品的概率是: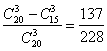 ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
6、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150 D154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是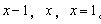 。那么有
。那么有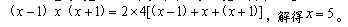 所以这个长方体的表面积为
所以这个长方体的表面积为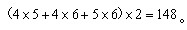
7、一根绳子对折三次后,从中剪断,共剪成几段绳子?_____
A: 9B: 6C: 5D: 3
参考答案: A 本题解释:正确答案是A考点计数模型问题解析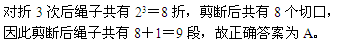
8、过长方体一侧面的两条对角线交点,与下底面四个顶点连得一四棱锥,则四棱锥与长方体的体积比为多少?_____
A: 1∶8B: 1∶6C: 1∶4D: 1∶3
参考答案: B 本题解释:【答案】B。解析:等底等高时,椎体体积是柱体的1/3。而这里椎体的高是柱体高的一半,因此该四棱锥与长方体的体积之比为1:6,故正确答案为B。
9、高速公路上行驶的汽车A的速度是每小时100公里,汽车B的速度是每小时120公里,此刻汽车A在汽车B前方80公里处,汽车A中途加油停车10分钟后继续向前行驶。那么从两车相距80公里处开始,汽车B至少要多长时间可以追上汽车A?_____
A: 2小时B: 3小时10分C: 3小时50分D: 4小时10分
参考答案: B 本题解释:正确答案是B考点行程问题解析汽车A在加油的10分钟时间内汽车B可行驶路程120×1/6=20公里,A、B间剩余80-20=60公里是A、B追及的过程,用时60÷(120-100)=3小时,因此汽车B追上A共用时3小时10分钟,故正确答案为B。
10、某车工计划15天里加工420个零件,最初3天中每天加工24个,以后每天至少要加工多少个才能在规定的时间内超额完成任务?_____
A: 31B: 29C: 30D: 28
参考答案: B 本题解释:【解析】B。(420-24×3)÷(15-3)=29
11、有甲、乙两只盒子,甲盒装有2个黑球、4个红球,乙盒装有4个黑球、3个红球,若从甲、乙两盒中各任取两球交换后,甲盒中恰有4个红球的概率为多少?_____
A:  B:
B: 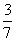 C:
C: 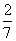 D:
D: 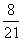
参考答案: D 本题解释:参考答案 题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有
题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有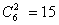 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有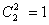 种,“1黑1红”的情形有
种,“1黑1红”的情形有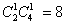 种,“2红”的情形有
种,“2红”的情形有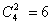 种;乙盒任取两个球:有
种;乙盒任取两个球:有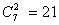 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有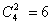 种,“1黑1红”的情形有
种,“1黑1红”的情形有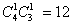 种,“2红”的情形有
种,“2红”的情形有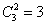 种。所以,“2黑”交换:
种。所以,“2黑”交换: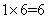 种;“1黑1红”交换:
种;“1黑1红”交换: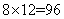 种;“2红”交换:
种;“2红”交换: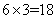 种;因此,甲盒中恰有4个红球的概率是:
种;因此,甲盒中恰有4个红球的概率是: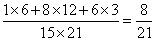 ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
12、某专业有学生50人,现开设有甲、乙、丙三门选修课。有40人选修甲课程,36人选修乙课程,30人选修丙课程,兼选甲、乙两门课程的有28人,兼选甲、丙两门课程的有26人,兼选乙、丙两门课程的有24人,甲、乙、丙三门课程均选的有20人,问三门课程均未选的有多少人?_____
A: 1人B: 2人C: 3人D: 4人
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析设选修甲课程的为集合A,选修乙课程的为集合B,选修丙课程的为集合C,根据三集合容斥原理公式:A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C,可得A∪B∪C=40+36+30-28-26-24+20=48,即至少选一门课的有48人,因此三门课程均未选的有:50-48=2,故选择B选项。秒杀技
13、某人买钢笔和铅笔合计18支,共用30元,钢笔每支8元,铅笔每支0.4元,钢笔和铅笔各多少支?_____
A: 3,15B: 4,14C: 6,12D: 8,10
参考答案: A 本题解释:参考答案:A题目详解:解法一:设钢笔有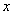 支,铅笔有
支,铅笔有 支,则
支,则 解得
解得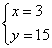 解法二:根据题意,假设全是铅笔,则:钢笔有:
解法二:根据题意,假设全是铅笔,则:钢笔有: 支,铅笔有:
支,铅笔有: 支。所以,选A。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
支。所以,选A。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
14、将两位数的个位数与十位数互换后所得的数是原来的十分之一,这样的两位数有多少个?_____
A: 6B: 9C: 12D: 15
参考答案: B 本题解释:B【解析】设原数字的个位数字为x,十位数字为y,则得:(10y+x)X1/10=10x+y化简得x=0个位数字是0的两位数有10,20,30,40,50,60,70,80,90,共9个,故正确答案为B。
15、某网店连续3次下调某款手机的零售价格,每次下调幅度分别为:2.7%、5.5%和4.6%。经过3次调价,该款手机零售价较下调前大约下降了_____。
A: 12.3%B: 12.8%C: 13.3%D: 13.8%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析连续调价三次以后价格为原价的(1-2.7%)×(1-5.5%)×(1-4.6%)>(1-2.7%-5.5%-4.6%),因此下降的价格幅度小于原价的2.7%+5.5%+4.6%=12.8%,故正确答案为A。
16、1/3+1/15+1/35+1/63+1/99+1/143+1/195+1/255的值是_____。
A: 6/17B: 6/19C: 8/17D: 8/19
参考答案: C 本题解释:正确答案是C考点计算问题解析
17、正六面体的表面积增加96%,棱长增加多少?_____
A: 20%B: 30%C: 40%D: 50%
参考答案: C 本题解释:【答案】C。解析:根据几何等比放缩性质,表面积为原来的1.96倍时,棱长为原来的1.4倍,因此棱长增加了40%。故正确答案为C。
18、(2009年秋季福建省公务员录用考试行测真题) 的值是_____。
的值是_____。
A: 1B: 2C:  D: 3
D: 3
参考答案: B 本题解释:参考答案:B题目详解:依题意:应用因式分解法;进行分母有理化: ;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
;所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
19、有一块长为30米,宽为20米的长方形苗圃,里面等距离的栽满了小树苗,每棵小树苗之间的间隔为2米,这个苗圃里面最多可以栽多少棵小树苗?_____
A: 146B: 176C: 168D: 150
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可知本题为两端均植树问题。在长边上每隔2米栽一棵树,可以植树30÷2+1=16棵;在宽边上每隔2米栽一棵树,可以植树20÷2+1=11棵;所以苗圃内最多可以栽16×11=176棵小树苗。所以,选B考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树
20、大年三十彩灯悬,灯齐明光灿灿,数时能数尽,五五数时剩一盏,七七数时刚刚好,八八数时还缺三,请你自己算一算,彩灯至少有多少盏?_____
A: 21B: 27C: 36D: 42
参考答案: A 本题解释:参考答案:A本题得分:题目详解:题干告诉我们灯的数目能整除7,被5除余数为1,被8除余数为5。方法一:代入法求解方法二:用“层层推进法”先找出满足被5除时余数为1的最小数为:5+1=6;然后在6的基础上每次都加5直到满足被8除时余数为5为止,6+5+5+5=21,21刚好能整除7,故彩灯至少有21盏;所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
21、甲、乙两个厂生产同一种玩具,甲厂生产的玩具数量每个月保持不变,乙厂生产的玩具数量每个月增加一倍,已知一月份甲、乙两个厂生产的玩具总数是98件,二月份甲、乙两个厂生产的玩具总数是106件。那么乙厂生产的玩具数量第一次超过甲厂生产的玩具数量是在几月份?_____
A: 3月B: 4月C: 5月D: 7月
参考答案: C 本题解释:正确答案是C考点不等式分析问题解析
22、小张到文具店采购办公用品,买了红黑两种笔共66支。红笔定价为5元,黑笔的定价为9元,由于买的数量较多,商店给与优惠,红笔打八五折,黑笔打八折,最后支付的金额比核定价少18%,那么他买了红笔_____。
A: 36支B: 34支C: 32支D: 30支
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析解析1:设买红笔A支,黑笔B支,由题意得:A+B=66······(1)(5A+9B)×0.82=5A×0.85+9B×0.8······(2)由(2)式得B=5/6A,则A=66×[6/(6+5)]=36。解析2:红笔打八五折,黑笔打八折,总价打八二折,相当于红笔和黑笔都打八二折,设红笔A支,黑笔B支,则(0.85-0.82)×5A=(0.82-0.80)×9B,得B=5/6A,则A=66×[6/(6+5)]=36。故正确答案为A。
23、已知29832983…298302能被18整除,那么n的最小值是_____。
A: 4B: 5C: 6D: 7
参考答案: A 本题解释:【解析】18=2×9,这个多位数的个位上是2,满足被2整除,因此,只需考虑个位数字之和能否被9整除的问题。(2+9+8+3)×n+0+2=22n+2是9的倍数,22×4+2=90=9×10,那么n的最小值为4。
24、三种动物赛跑,已知狐狸的速度是兔子的2/3,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑_____米。
A: 28B: 14C: 19D: 7
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析根据题意,设兔子、狐狸、松鼠的速度比为6:4:3,一分钟松鼠比狐狸少跑14米,说明一份为14米/分钟,所以兔子和狐狸的速度分别为6×14和4×14,因此半分钟兔子比狐狸多跑(6×14-4×14)÷2=14米,故正确答案为B。秒杀技题目中时间为半分钟,实际上是一个时间陷阱,根据猜题技巧,选项中应有一个干扰选项是正确选项的2倍,只有A、B符合,即B项正确。标签猜题技巧
25、每条长200米的三个圆形跑道共同相交于A点,张三、李四、王五三个队员从三个跑道的交点A处同时出发,各取一条跑道练习长跑。张三每小时跑5公里,李四每小时跑7公里,王五每小时跑9公里。问三人第四次在A处相遇时,他们跑了多长时间?_____
A: 40分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: B 本题解释:【答案解析】分别求出跑1米所用的时间。60/5000=张三,60/7000=李四,60/9000=王五。张三跑完200米要12/5分钟(2.4),李四需要12/7(1.7)分钟,王五需要4/3(1.3)分钟。张与李圈相差0.7分钟,与王相差1.1分钟,李与王差0.6分钟。得出这样的关系后可以算出张跑到第N圈时(N>4)李和王刚好也在A点,他们2.4分钟时的位移分别为:200m、282m、365m,然后求出圈差的位移82M.165M然后用200分别除以82.165,求出李需要2.44次的2.4分钟就可以再跑200米,王需要1.2次的2.4分钟,然后通分求出共需要多少个2.4分钟就行了。
26、某班同学买了161瓶汽水,5个空瓶可以换一瓶汽水,他们最多可以喝到_____瓶汽水。
A: 200B: 180C: 201D: 199
参考答案: C 本题解释:参考答案:C题目详解:根据5个空瓶可以换一瓶汽水可知,4个空瓶=1瓶子汽水中的汽水,因此,最多可以换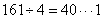 ,故最多喝
,故最多喝 瓶。因此,选C。(1)喝完的161瓶汽水空瓶可以换
瓶。因此,选C。(1)喝完的161瓶汽水空瓶可以换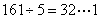 .喝完之后,剩下
.喝完之后,剩下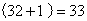 个空瓶;(2)33个空瓶可以换
个空瓶;(2)33个空瓶可以换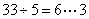 ,喝完之后,剩下
,喝完之后,剩下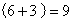 个空瓶;(3)9个空瓶可以换
个空瓶;(3)9个空瓶可以换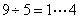 ,喝完之后,剩下
,喝完之后,剩下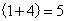 个空瓶;(4)5个空瓶可以换1瓶汽水。因此,最多可以:
个空瓶;(4)5个空瓶可以换1瓶汽水。因此,最多可以: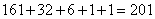 。因此,选C。(2)解法二:
。因此,选C。(2)解法二: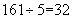 余1,
余1,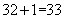 ,
,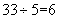 余3,
余3,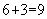 ,
,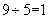 余4,和别人借一个
余4,和别人借一个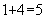 ,正好再换一瓶,喝完再还给他。一共喝了
,正好再换一瓶,喝完再还给他。一共喝了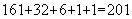 瓶。考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
瓶。考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
27、有甲、乙两只装满水的圆柱形玻璃杯,杯的内半径分别是5厘米、8厘米,甲杯中此前放一铁块,当取出此铁块时,甲杯中的水位下降了3厘米,然后将此铁块放入乙杯中。这时乙杯中的水位上升了多少厘米?_____
A: 4厘米B: 1厘米C: 0.5厘米D: 0厘米
参考答案: D 本题解释:正确答案是D考点几何问题解析因为乙杯已经装满水,所以无论加入什么,乙杯的水位都不会发生变化。故正确答案为D。
28、某汽车厂离生产甲、乙、丙三种车型,其中乙型产量的3倍与丙型产量的6倍之和等于甲型产量的4倍,甲型产量与乙型的2倍之和等于丙型产量的7倍。则甲、乙、丙三型产量之比为_____。
A: 5:4:3B: 4:3:2C: 4:2:1D: 3:2:1
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设甲的产量为x,乙的产量为y,丙的产量为z。则可得如下:3y+6z=4x,x+2y=7z,两式相加可得3x+z=5y,直接带入选项,只有D符合,故正确答案为D。秒杀技得到3y+6z=4x后,观察该式,可知x应为3的倍数,只有D符合。标签直接代入
29、在400米环形跑道上,A、B两点最近相距100米(如图)。甲、乙两位运动员分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑9米,乙每秒7米,他们每人跑100米都停5秒,那么追上乙需要多少秒?_____ 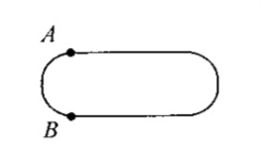
A: 70B: 65C: 75D: 80
参考答案: D 本题解释:参考答案D题目详解:甲每跑100/9秒休息5秒:跑100米需l00/9+5=145/9秒;同理:乙跑100米需100/7+5=135/7秒;75秒时,甲休息了四次:共跑(75-4×5)×9=495米;乙正在休息第四次,共跑100/7×7×4=400米,甲并没有追上乙。所以甲追上乙的时间应大于75秒,所以,选D。考查点:数量关系>数学运算>行程问题>追及问题>环线追及问题>环线一次追及问题
30、某城市共有A、B、C、D、E五个区,A区人口是全市人口的5/17,B区人口是A区人口的2/5,C区人口是D区和E区人口总数的5/8,A区比C区多3万人,全市共有多少万人?_____
A: 20.4B: 30.6C: 34.5D: 44.2
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由A区人口是全市人口的5/17,将全市人口看做17份,则A区有5份,B区有2份,于是C、D、E三区共有10份,而在此三区中,C区人口是D区和E区人口总数的5/8,也即C区人口是此三区人口总数的5/13,因此C区人口为(5/13×10)份,于是A区比C区多5-50/13=15/13份,此部分人口数为3万人,于是全市共有3÷15/13×17=44.2(万人)。故正确答案为D。标签赋值思想
31、已知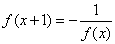 ,若
,若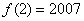 ,
,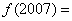 _____
_____
A: 2B:  C:
C:  D: 2008
D: 2008
参考答案: B 本题解释:参考答案:B题目详解:根据题干可得: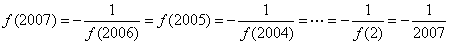 ,答案B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
,答案B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
32、一列客车长250米,一列货车长350米,在平行的轨道上相向行驶,从两车头相遇到两车尾相离经过15秒,已知客车与货车的速度比是5:3。问两车的速度相差多少?_____
A: 10米/秒B: 15米/秒C: 25米/秒D: 30米/秒
参考答案: A 本题解释:正确答案是A考点行程问题解析两车头相遇到两车尾相离相当于两车车尾相遇过程,设两车速度为5v、3v,则有15×(5v+3v)=250+350,解得v=5,因此两车速度相差5v-3v=2v=10米/秒。标签赋值思想比例转化
33、筑路队原计划每天筑路720米,实际每天比原计划多筑路80米,这样在规定完成全路修筑任务的前3天,就只剩下1160米未筑,这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释:C解析:现在每天筑路:720+80=800(米)规定时间内,多筑的路是:(720+80)×3-1160=2400-1160=1240(米)求出规定的时间是1240÷80=15.5(天),这条路的全长是720×15.5=11160(米)。故本题选C。
34、已知A、B是河边的两个口岸。甲船由A到B上行需要10小时,下行由B到A需要5小时。若乙船由A到B上行需要15小时,则下行由B到A需要_____小时。
A: 4B: 5C: 6D: 7
参考答案: C 本题解释:参考答案:.C题目详解:解法一:根据题意,设甲船速度为a,水流速度为b,乙船速度为c,乙船由B到A要时间t,AB间距离为s,则有:甲船的上行速度为: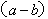 ,甲船的下行速度为:
,甲船的下行速度为: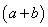 ;乙船的上行速度为:
;乙船的上行速度为: ,乙船的下行速度为:
,乙船的下行速度为: ;那么,则有:
;那么,则有: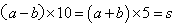 ,化简得
,化简得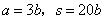 ;
;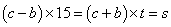 ,
,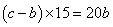 ,得
,得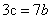 ;代入
;代入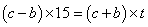 ,解得t=6所以,选C。解法二:根据漂流瓶问题核心公式,设乙船从B到A下行需要
,解得t=6所以,选C。解法二:根据漂流瓶问题核心公式,设乙船从B到A下行需要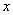 小时:
小时: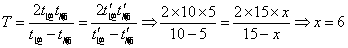 (小时)所以,选C。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
(小时)所以,选C。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
35、甲从A地,乙从B地同时以均匀的速度相向而行,第一次相遇离A地6千米,继续前进,到达对方起点后立即返回,在离B地3千米处第二次相遇,则A,B两地相距多少千米? (D)
A: 10B: 12C: 18D: 15
参考答案: D 本题解释:答案:D 解析:设A,B两地相距为y千米,6/(y-6)=(y-6+3)/(6+y-3),解得y=15。
36、加油站有150吨汽油和102吨柴油,每天销售12吨汽油和7吨柴油。问多少天后,剩下的柴油是剩下的汽油的3倍?_____
A: 9B: 10C: 11D: 12
参考答案: D 本题解释:【答案】D。解析:假设x天,汽油还剩150-12x,柴油还剩102-7x,102-7x=3(150-12x),解得x=12,答案为D。
37、一只装有动力桨的船,其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划动从A地顺流到达B地,原路返回时只开足动力桨行驶,用时比来时少2/5。问船在静水中开足动力浆行驶的速度是人工划船速度的多少倍?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:B[解析]设水速是1,则顺水速度为3,人工划船静水速度=3-1=2,顺水时间:逆水时间=1: (1-2/5)=5:3,则顺水速度:逆水速度=3:5,所以逆水速度为5,动力桨静水速度=5+1=6,比例为6:2=3:1
38、有5个数的算术平均数为25,去掉其中一个数后,算术平均数为31,试问去掉的那个数是多少?_____
A: 4B: 3C: 1D: 2
参考答案: C 本题解释:参考答案:C题目详解:解法一: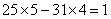 (尾数法)。解法二:依题意:设去掉的那个数为
(尾数法)。解法二:依题意:设去掉的那个数为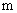 ,剩余四个数和为
,剩余四个数和为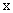 ;则5个数之和为25,可得:
;则5个数之和为25,可得: ;则去掉一个数
;则去掉一个数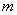 之后平均值:
之后平均值: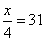 ,解方程得:
,解方程得: ;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
39、某市居民用电实行分段式收费,以人为单位设定了相同的基准用电度数,家庭人均用电量超过基准用电度数的部分按照基准电费的两倍收取电费。某月,A家庭5口人用电250度,电费175元;B家庭3口人用电320度,电费275元。该市居民每人的基准用电为_____度。
A: 50B: 35C: 30D: 25
参考答案: C 本题解释:正确答案是C考点分段计算问题解析设每人基准用电为m,基准电费为n,则可得方程组如下:n×5m+2n×(250-5m)=175,n×3m+2n×(320-3m)=275,联立解得m=30。故正确答案为C。
40、符号消费是指在消费过程中,消费者除消费产品本身以外,同时也消费这些产品所象征和代表的意义、心情、美感、档次、情调和气氛,即对这些符号所代表的“意义”或“内涵”的消费。根据上述定义,下列各项中体现了符号消费的是_____。
A: 大张和小伟结伴去背包旅行,小伟买了个专业登山包,大张随便背了个包就去了,结果被小伟嘲笑了一番B: 面点师小金每到一个地方,都会去当地知名的蛋糕店点上几份甜品,并且花上几个小时仔细品尝C: 某甜品店最近生意火爆,顾客都指明要该店新推出的一款特色饮品D: 老李退休后非常注重养生,买了一大堆的保健品
参考答案: A 本题解释:A。定义的关键词是“意义”和“内涵”。A项,小伟和大张的包都能够满足旅行的需要,但小伟嘲笑大张的包,说明他购买专业登山包,主要是消费它所代表的时尚、档次等“内涵”,并不是在于包本身,因此符合定义。B项,小金作为面点师,去仔细品尝知名蛋糕店的甜品,是为了改进、提高自己的手艺,而不单纯是为了消费,因而也就更谈不上是符号消费。C项,顾客购买新推出的特色产品,针对的是产品本身。D项,老李购买保健品是出于养生的需求,他消费的也是产品本身。
41、有5位田径运动员争夺3项比赛的冠军,若每项只设1名冠军,则获得冠军的情况可能有_____。
A: 124种B: 125种C: 130种D: 243种
参考答案: B 本题解释: B [解析] 每项比赛的冠军都有5种可能性,所以获得冠军的情况有C15×C15×C15=125(种)。故本题选B。
42、一位长寿老人生于19世纪90年代,有一年他发现自己的年龄的平方刚好等于当年的年份。问这位老人出生于哪一年?_____
A: 1894年B: 1892年C: 1898年D: 1896年
参考答案: B 本题解释:正确答案是B考点年龄问题解析由于年龄的平方等于当年的年份,而年份介于1890到2010之间,所以该老人应该是40多岁,而已知:43的平方为1849,44的平方为1936,45的平方为2025。因此,该老人在1936年应为44岁,1936-44=1892。故正确答案为B。
43、阳光下,电线杆的影子投射在墙面及地面上,其中墙面部分的高度为1米,地面部分的长度为7米。甲某身高1.8米,同一时刻在地面形成的影子长0.9米。则该电线杆的高度为_____。
A: 12米B: 14米C: 15米D: 16米
参考答案: C 本题解释:正确答案是C考点几何问题解析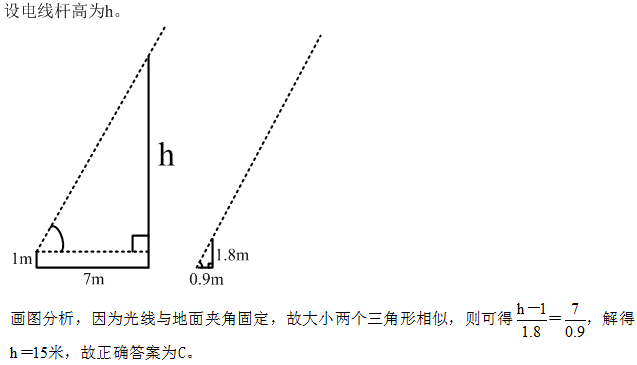 标签几何等比放缩性质
标签几何等比放缩性质
44、火车驶过长900米的铁路桥,从车头上桥到车尾离桥共用1分25秒,紧接着列车又穿过一条长1800米的隧道,从车头进隧道到车尾离开隧道用了2分40秒,则火车车身长为_____。
A: 120米B: 100米C: 80米D: 90米
参考答案: A 本题解释:参考答案:A题目详解:应用方程法:由于火车速度相同,设车身长度为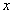 米;从车头上桥到车尾离桥火车行驶距离为:
米;从车头上桥到车尾离桥火车行驶距离为: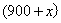 米;从车头进遂道到车尾离开遂道行驶距离为:
米;从车头进遂道到车尾离开遂道行驶距离为: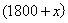 米;列方程:
米;列方程: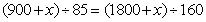 ,解
,解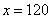 米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
45、一段路程分为上坡、平路、下坡,三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米,路程全长是50千米,小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析:上坡、平路、下坡的速度之比是:14∶25∶36=5∶8∶10平路速度为:3×8/5=24/5(千米/小时)下坡速度为:3×10/5=6(千米/小时)上坡路程为:50×1/(1+2+3)=50/6=25/3(千米)平路路程为:50×2/(1+2+3)=50/3(千米)下坡路程为:50×3/(1+2+3)=25(千米)小龙走完全程用的时间为:25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。
46、某玩具店同时卖出一个拼装玩具和一架遥控飞机,拼装玩具66元,遥控飞机120元,拼装玩具赚了10%,而遥控飞机亏本20%,则这个商店卖出这两个玩具赚钱或是亏本多少_____
A: 赚了12元B: 赚了24元C: 亏了14元D: 亏了24元
参考答案: D 本题解释:D【解析】根据题意,拼装玩具赚了66÷(1+10%)×10%=6元,遥控飞机亏本120÷(1-20%)×20%=30元,故这个商店卖出这两个玩具亏本30-6=24元。
47、有5位田径运动员争夺3项比赛的冠军,若每项只设1名冠军,则获得冠军的情况可能有_____。
A: 124种B: 125种C: 130种D: 243种
参考答案: B 本题解释: B [解析] 每项比赛的冠军都有5种可能性,所以获得冠军的情况有C15×C15×C15=125(种)。故本题选B。
48、某市规定,出租车合乘部分的车费向每位乘客收取显示费用的60%,燃油附加费由合乘客人平摊。现有从同一地方出发的三位客人合乘,分别在D、E、F点下车,显示的费用分别为10元、20元、40元,那么在这样的合乘中,司机的营利比正常(三位客人是一起的,只是分别在上述三个地方下车)多_____。
A: 1元B: 2元C: 10元D: 12元
参考答案: C 本题解释:正确答案是C考点分段计算问题解析第一位下车客人为合乘,涉及金额为10元;第二位下车客人为合乘,涉及金额为20元;第三位下车客人合乘部分涉及金额20元,独乘部分涉及金额为20元;所以实际营利为10×60%+20×60%+20×60%+20=50元,比正常多50-40=10元。故正确答案为C。标签分类分步
49、五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩,其中语文成绩优秀的有65人,数学成绩优秀的有87人。语文、数学都优秀的有多少人?_____
A: 30B: 35C: 57D: 65
参考答案: A 本题解释:参考答案:A题目详解:此题是典型的两个集合的容斥问题,由题意设:A={{语文成绩优秀的人}};B={{数学成绩优秀的人}};因此,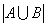 ={{五年级参加语文、数学考试的人}};
={{五年级参加语文、数学考试的人}}; ={{语文和数学都优秀的人}}由两个集合的容斥原理可得:
={{语文和数学都优秀的人}}由两个集合的容斥原理可得: =
=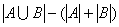 =
=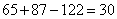 所以,选A。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
所以,选A。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
50、有甲、乙两根水管,分别同时给A、B两个大小相同的水池注水,在相同的时间里甲、乙两管注水量之比是 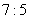 。经过
。经过 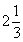 小时,A、B两池中注入的水之和恰好是一池。这时,甲管注水速度提高
小时,A、B两池中注入的水之和恰好是一池。这时,甲管注水速度提高 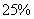 ,乙管的注水速度不变,那么,当甲管注满A池时,乙管再经过多少小时注满B池?_____
,乙管的注水速度不变,那么,当甲管注满A池时,乙管再经过多少小时注满B池?_____
A: 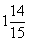 B:
B: 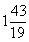 C: 1D:
C: 1D: 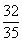
参考答案: A 本题解释:参考答案:A题目详解:根据题意,设水池容积为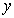 ,甲管每小时注水
,甲管每小时注水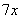 ,乙管每小时注水
,乙管每小时注水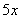 。则
。则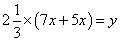 ,得到
,得到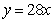 ;甲已经灌了
;甲已经灌了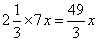 ,还剩下
,还剩下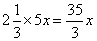 ,此时甲管注水速度提高
,此时甲管注水速度提高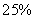 ,甲每小时注水速度为
,甲每小时注水速度为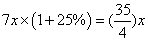 ,因此甲注满水池还需要:
,因此甲注满水池还需要: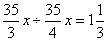 时;乙最开始灌了
时;乙最开始灌了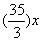 ,还剩
,还剩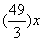 ,保持原速度的话当甲灌满水池时乙灌了
,保持原速度的话当甲灌满水池时乙灌了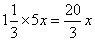 ,还差
,还差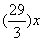 ,乙还需要
,乙还需要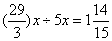 小时才可注满B池。因此,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
小时才可注满B池。因此,选A。考查点:数量关系>数学运算>工程问题>合作完工问题
51、某单位有60名运动员参加运动会开幕式,他们着装白色或黑色上衣,黑色或蓝色裤子。其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人?_____
A: 12B: 14C: 15D: 19
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析解析1:穿白色上衣的有60-29=31人,其中穿白上衣黑裤子的有31-12=19人,穿黑上衣黑裤子的有34-19=15人。解析2:设白上衣黑裤子有a人,黑上衣黑子裤有b人,黑上衣蓝裤子有c人,根据题意有a+b+c=60-12,a+b=34,b+c=29,则b=34+29-(60-12)=15人。故正确答案为C。
52、 _____
_____
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点计数模型问题解析 故正确答案为C。标签公式应用
故正确答案为C。标签公式应用
53、_____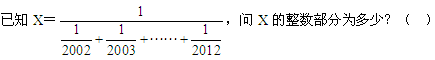
A: 182B: 186C: 194D: 196
参考答案: A 本题解释:正确答案是A考点不等式分析问题解析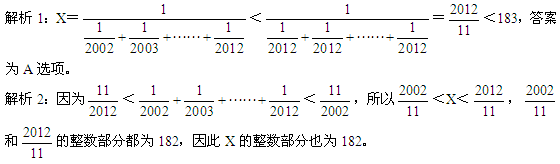 故正确答案为A。
故正确答案为A。
54、某商店花10000元进了一批商品,按期望获得相当于进价25%的利润来定价,结果只销售了商品总量的30%,为尽快完成资金周转,商店决定打折销售,这样卖完全部商品后,亏本1000元,问商店是按定价打几折销售的?_____
A: 九折B: 七五折C: 六折D: 四八折
参考答案: C 本题解释:正确答案是C考点经济利润问题解析解析1:某商品进该批产品成本为10000元,其中30%是按照相当于进价25%的利润定价,也即3000元的部分是按此利润售出的,此部分回收资金为3000×1.25=3750(元)。根据亏本1000元,可知总共收回资金为9000元,因此剩下的7000元商品实际只售出9000-3750=5250(元),故折扣为5250÷(7000×1.25)=0.6,也即6折。故正确答案为C。解析2:设一共有10件商品,折扣为Y,则每件商品进价为1000元,利润为250元,可列方程1250×3+1250Y×7=9000,解得Y=0.6,故正确答案为C。标签赋值思想
55、甲、乙两人玩打赌游戏,连续抛三个硬币,如果同时出现正面或同时出现反面算乙输,出现两个正面或两个反面算甲输,若甲输,则甲要给乙10元,问:乙输要给甲多少,甲才肯玩游戏?_____
A: 10元B: 15元C: 20元D: 30元
参考答案: D 本题解释:参考答案 题目详解:连续抛三个硬币,同时出现正面或反面的概率是:
题目详解:连续抛三个硬币,同时出现正面或反面的概率是: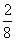 即
即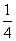 ;出现两个正面或两个反面的概率是:
;出现两个正面或两个反面的概率是: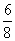 即
即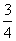 ;可见甲输的概率是乙输的概率的3倍;因此乙若输,则需要给甲
;可见甲输的概率是乙输的概率的3倍;因此乙若输,则需要给甲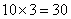 (元),甲才肯玩这个游戏;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
(元),甲才肯玩这个游戏;所以,选D。考查点:数量关系>数学运算>概率问题>单独概率
56、小陈、小张、小赵和小周四个人的平均基本工资为1010元,这次工资调整,他们基本工资分别上调了254元、191元、146元和209元,现在四个人的平均基本工资是_____
A: 1180元B: 1210元C: 1080元D: 1220元
参考答案: B 本题解释: 【解析】B。现在平均基础工资为1010+(254+191+146+209)÷4=1210元。
57、(2007北京应届,第24题)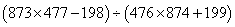 的值是_____。
的值是_____。
A: 1B: 2C: 3D: 4
参考答案: A 本题解释:参考答案:A题目详解:解法一:鉴于题中数字两两相近,可以采用整体消去法:原式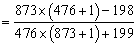
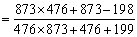
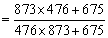 =1;所以,选A。解法二:
=1;所以,选A。解法二:
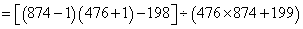
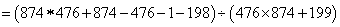
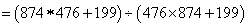 =1;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
=1;所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
58、有两个三口之家一起出行去旅游,他们被安排坐在两排相对的座位上,其中一排有3个座位,另一排有4个座位。如果同一个家庭成员只能被安排在同一排座位相邻而坐,那么共有多少种不同的安排方法?_____
A: 36B: 72C: 144D: 288
参考答案: C 本题解释:正确答案是C考点排列组合问题解析
59、一只猫每天吃由食品 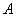 和食品
和食品 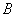 搅拌成的食物
搅拌成的食物 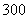 克,食品
克,食品 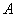 的蛋白质含量为
的蛋白质含量为 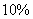 ,食品
,食品 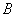 的蛋白质含量为
的蛋白质含量为 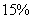 。如果该猫每天需要
。如果该猫每天需要 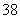 克蛋白质,问食物中食品
克蛋白质,问食物中食品 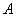 的比重是百分之几?_____
的比重是百分之几?_____
A: 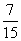 B:
B: 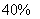 C:
C: 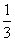 D:
D: 
参考答案: A 本题解释:参考答案:A题目详解:应用方程法:设 的比重为
的比重为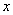 ,可列方程:
,可列方程: ,解得
,解得 ;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合
;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合
60、两工厂各加工480件产品,甲工厂每天比乙工厂多加工4件,完成任务所需时间比乙工厂少10天。设甲工厂每天加工产品x件,则x满足的方程为_____。
A: 480/x+10=480/(x+4)B: 480/x-10=480/(x+4)C: 480/x+10=480/(x-4)D: 480/x-10=480/(x-4)
参考答案: C 本题解释:正确答案是C考点工程问题解析根据题意得:甲完成需要480/x天,乙完成需要480/(x-4)天,则完成时间的等量关系为480/x+10=480/(x-4)。故正确答案为C。
61、甲、乙两人共储蓄1000元,甲取出240元,乙又存入80元,这时甲的储蓄正好是乙的3倍,原来甲比乙多储蓄多少元?_____
A: 620元B: 740元C: 700元D: 660元
参考答案: B 本题解释:正确答案:B解析:假设甲储蓄的钱为X,则乙为1000-X,那么X-240=3(1000-X+80),X=870,则乙为1000-870=130。甲比乙多870-130=740元。故答案为B。
62、三位数的自然数N满足:除以6余3,除以5余3,除以4也余3,则符合条件的自然数N有几个?_____
A: 8B: 9C: 15D: 16
参考答案: C 本题解释:正确答案是C考点余数与同余问题解析由题意可知满足同余情形,例如此题”三位自然数N除以6余3,除以5余3,除以4也余3”,可见余数恒为3,则取3,因此N的表达式为60n+3,其中60为6、5、4的最小公倍数,根据题目中的N为三位数,可得不等式100≤60n+3≤999,解得2≤n≤16,因此符合条件的自然数有15个,故正确答案为C选项。注:同余问题需要如下口诀:余同取余,和同加和,差同减差,最小公倍数做周期。口诀解释:余同取余,例如本题,余数恒为3,则取3;合同加和,例如”一个数除以7余1,除以6余2,除以5余3”,可见除数与余数的和相同,取此和8,被除数的表达式为210n+8;差同减差,例如”一个数除以7余3,除以6余2,除以5余1”。可见除数和余数的差相同,取此差4,被除数的表达式为210-4,其中210为5、6、7的最小公倍数。秒杀技根据题目,符合要求的数出现的周期为6、5、4的最小公倍数60,也即每60个连续自然数中必然有一个符合要求,三位数共有900个,因此符合要求的三位数共有900÷60=15(个),故正确答案为C选项。标签最小公倍数同余问题
63、用12米长的篱笆围成一个一边是墙的矩形鸡场,要使鸡场的面积最大,矩形的面积应是:_____
A: 3B: 6C: 8D: 18
参考答案: D 本题解释:参考答案 题目详解:设矩形的宽为x米,长为(12-2x)米:则面积S=x(12-2x)=-2(x-3)2+18;则长为6米;即当长为6米时,鸡场的最大面积为18平方米。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
题目详解:设矩形的宽为x米,长为(12-2x)米:则面积S=x(12-2x)=-2(x-3)2+18;则长为6米;即当长为6米时,鸡场的最大面积为18平方米。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
64、_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点几何问题解析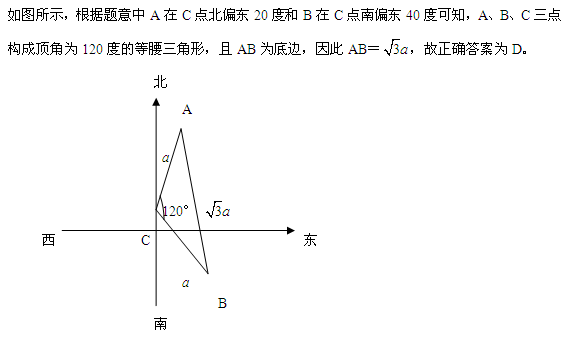 标签画图分析
标签画图分析
65、某中学给住校生分配宿舍,如果每个房间住3人,则多出20人,如果每个房间住5人,则有2间没人住,其他房间住满。则总共有多少人是住校生?_____
A: 60B: 65C: 70D: 75
参考答案: B 本题解释:【答案】B。解析:显然在每间房3人的基础上增加2人,不仅包括了多出的人,还包括了空出的2间共10人,因此房间数为30÷2=15(间),因此总人数为15×3+20=65(人)。
66、一批木材全部用来加工桌子可以做30张,全部用来加工床可以做15张。现在加工桌子、椅子和床各2张,恰好用去全部木材的1/4。剩下的木材全部用来做椅子,还可以做多少把?_____
A: 40把B: 30把C: 25把D: 5把
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由题意得每张桌子用这批木材的1/30,每张床用这批木材的1/15,则加工一把椅子用去木材的1/4÷2-1/30-1/15=1/40,故剩余的3/4木材还可做椅子3/4÷1/40=30把,正确答案为B。
67、一个农贸市场2斤油可换5斤肉,7斤肉可换12斤鱼,10斤鱼可换21斤豆,那么27斤豆可换几斤油?_____
A: 3B: 4C: 5D: 6
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析
68、商店里有六箱货物,分别重15、16、18、19、20、31千克,两个顾客买走了其中五箱,已知一个顾客买的货物重量是另一个顾客的2倍。商店剩下的一箱货物重多少千克_____
A: 16B: 18C: 19D: 20
参考答案: D 本题解释: 【解析】D。由题可知卖出的五箱货物一定能被3整除,六箱货物的总重为119千克,只有D项能使五箱货物被3整除,故选D。
69、甲乙两人的岁数的和是一个两位的质数。这个质数的数字之和等于13,甲比乙也大13岁,问甲多少岁,乙多少岁?_____
A: 27,40B: 20,33C: 40,53D: 23,36
参考答案: A 本题解释:参考答案:A题目详解:因为这个两位数的数字和等于13:13=9+4=8+5=7+6;又因为和是一个两位数的质数:组成的两位数字中只有67是质数,所以这个和是67;根据和差问题的解法:甲比乙大13岁,甲的年龄:(67+13)÷2=40岁;乙的年龄:40-13=27岁。所以选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
70、王家村西瓜大丰收后,全村男女老少分四个组品尝西瓜,且每组人正好一样,小伙子一个人吃1个,姑娘两个人吃1个,老人三个人吃1个,小孩四个人吃1个,一共吃了200个西瓜,问王家村品尝西瓜的共有_____
A: 368人B: 384人C: 392人D: 412人
参考答案: B 本题解释: B。方法一:利用整除关系。答案必须是2,3,4的公倍挚,也就是说答案必须是12的整数倍数。只有B满足。方法二:假设每组有x人。x+x/2+x/3+x/4=200,解得x=96,96×4=384(人)。
71、有6张卡片,分别写着数字1,2,5,6,8,9。现在从中取出3张卡片,并排放在一起,组成一个三位数。问可以组成多少个不同的偶数?_____
A: 144个B: 120个C: 60个D: 12个
参考答案: C 本题解释: 
72、某考试均为判断题,共10题,每题10分,满分为100分。考生答题时认为正确则画为“0”。认为不正确则画“×”。以下是考生的答题情况及甲、乙、丙的实际得分,则丁的得分为_____。题号12345678910得分甲××0×0××0××0乙×000×0×0000丙×000×××0×00丁××000××0000
A: 20分B: 40分C: 60分D: 80分
参考答案: C 本题解释:【答案】C。解析:首先观察甲和丙,得分相差40分,而他们的答案不一样的出恰好有4题,那么也就是说,丙和甲不一样的题(即2,4,5,10)甲都做对了,而这四道题恰好乙也全做错了,而乙一共做错了5道题,也就是说剩下的题目(1,3,7,8,6,9)中,乙只错了一个;又四人判断一致的题目,(即1,3,7,8)中必有一个四个人全做错了,因为丙一共只做对了3道题,那么,也就是说6、9、题乙做对了,那么现在答案除了1、3、7、8都确定了,即(2,4,5,10)与甲一致,(6,9)与乙一致,在这6道题中丁做对了3道,剩下的(1,3,7,8)丁做对3道。综上所述,丁得分60分。
73、甲、乙、丙三个班向希望工程捐赠图书,已知甲班有1人捐6册,有2人各捐7册,其余各捐11册,乙班有1人捐6册,有3人各捐8册,其余各捐10册,丙班有2人捐4册,6人各捐7册,其余人各捐9册。已知甲班捐书总数比乙班多28册,乙班比丙班多101册,各班捐书总数在400~550册之间。那么,甲、乙、丙三个班各有多少人?_____
A: 48、50、53B: 49、51、53C: 51、53、49D: 49、53、51
参考答案: C 本题解释:正确答案是C考点和差倍比 问题解析甲班比丙班多28+101=129册,则甲班总数在529—550之间;甲班为6+2×7+11n=20+11n,多捐2册就能被11整除,所以甲班总数只能是548(550-2)或537,因此丙班是419或408;丙班为2×4+6×7+9m=50+9m,多捐4册就能被9整除。因此丙班捐了419本,则丙班有(419-50)÷9+8=49人,故正确答案为C。
74、两个相同的瓶子装满酒精溶液,一个瓶子中酒精与水的体积比是3:1,另一个瓶子中酒精与水的体积比是4:1,若把两瓶酒精溶液混合,则混合后的酒精和水的体积之比是多少?_____
A: 31:9B: 7:2C: 31:40D: 20:11
参考答案: A 本题解释:正确答案是A考点其他解析设两个瓶子每个容量为20,第一个瓶子中酒精和水分别为15和5;另一个瓶子中酒精和水分别为16和4,混合后酒精和水体积比为(15+16):(5+4)=31:9,故正确答案为A。
75、一条双向铁路上有11个车站,相邻两站都相距7千米。从早晨7点,有18列货车由第11站顺次发出,每隔5分钟发一列,都驶向第一站,速度都是每小时60千米;早晨8点,由第1站发一列客车,向第11站驶出,时速100千米,在到达终点前,货车与客车都不停靠任何一站。那么,在_____,客车能与3列货车先后相遇。
A: 在第四、五站之间B: 在第五、六站之间C: 在第六、七站之间D: 在第七、八站之间
参考答案: B 本题解释:正确答案是B考点行程问题解析铁路上共有11个站,相邻两站相距7千米,则共有70千米的距离,每辆货车之间的距离是5千米。早晨8点,第一列货车已经开出60千米,与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米,之后每行驶3.125公里即相遇一列货车,则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇,则这三列货车中的第一列与客车相遇的地点距离站点不超过:7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75,取n=7时商为4,余数为0.125<0.75。则客车行驶在第五、六站之间,分别和第8、9、10辆货车相遇。故正确答案为B。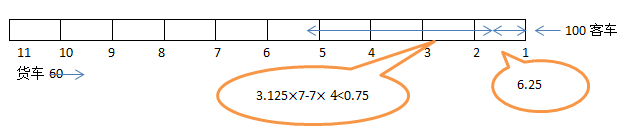 标签画图分析
标签画图分析
76、有一种数叫做完全数,它恰巧等于除去它本身以外的一切因数的和,如6是因数1+2+3的和。请问在20到30之间,这样的完全数是哪个?_____
A: 24B: 26C: 27D: 28
参考答案: D 本题解释:参考答案 题目详解:根据题意,采用代入法对各项分析,只有28=1+2+4+7+14,其他选项都不符合题意。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
题目详解:根据题意,采用代入法对各项分析,只有28=1+2+4+7+14,其他选项都不符合题意。所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
77、一串数排列成一行,它们的规律是这样的:前两个数都是1,从第三个数开始,每个数是它前两个数的和,也就是:1,1,2,3,5,8,13,21,34,…问:这串数的前100个数中有多少个偶数?_____
A: 33B: 32C: 50D: 39
参考答案: A 本题解释:参考答案:A题目详解:依题意:“1,1,2,3,5,8 ”根据“奇偶相加法则”:这个数列以“奇、奇、偶”为周期,循环出现;周期
”根据“奇偶相加法则”:这个数列以“奇、奇、偶”为周期,循环出现;周期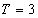 ;前99个数中有33个偶数:而第100个数是奇数。共33个偶数。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
;前99个数中有33个偶数:而第100个数是奇数。共33个偶数。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
78、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人,可知乙培训过的人数含有因子3,而总的培训人数1290也含有因子3,因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人,因此要使甲教室培训过的人数也含有3因子,则其举办次数必然含有3因子,因此只有C、D符合。将C选项代入,可知此时乙教室举办过15次培训,其总人数的尾数为5,而甲教室培训的总人数尾数总是为0,因此甲、乙教室的培训人数尾数为5,不符合要求。故正确答案为D。秒杀技由题意,甲教室每次培训50人,乙教室每次培训45,假设甲乙的次数分别为X、Y,则可得50X+45Y=1290,观察等式可知45Y的尾数必然为0,因此Y必然为偶数,从而X为奇数,仅D符合。故正确答案为D。
79、173×173×173-162×162×162=_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:D【解析】利用简单的猜测法。173的尾数是3,3的立方为27;162的尾数是2,2立方为8。两者相减尾数为9,所以判断173和162的立方之差的尾数为9。所以答案为D项。
80、2011×201+201100—201.1×2910的值为_____。
A: 20110B: 21010C: 21100D: 21110
参考答案: A 本题解释:原式=2011×(201+100—291)=2011×10=20110。故选A。
81、某小区物业征集业主意见,计划从100户业主中抽取有20户进行调查。100户业主中有b户主年龄超过60岁,a户户主年龄不满35岁,户主年龄在36岁到59岁的有25户。为了使意见更具代表性,物业采取分层抽样的方法,从b户中抽取了4户,则a的值可能是_____。
A: 55B: 66C: 44D: 50
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析100户中抽取20户,可知抽取比例为5:1,根据题意,4:b=20:100,a+b=75,解得a=55。故答案为A。
82、某品牌啤酒可以用3个空瓶再换回1瓶啤酒,某人买回10瓶啤酒,则他最多可以喝到_____瓶啤酒。
A: 13B: 15C: 16D: 17
参考答案: B 本题解释:参考答案:B题目详解:9瓶可以换到3瓶啤酒回来,这时候剩下买10瓶当中的1个空瓶,以及喝完3瓶啤酒的空瓶,总共4个空瓶,再用3个空瓶换1瓶,剩下两个空瓶,向卖家借1瓶啤酒喝完还给他3个空瓶,因此总共是: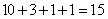 ;简便法:3瓶换1瓶实际上是只需要2个瓶子,因此买10瓶能够换到
;简便法:3瓶换1瓶实际上是只需要2个瓶子,因此买10瓶能够换到 5瓶,
5瓶, 考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
83、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8B: 10C: 12D: 15
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人,可知乙培训过的人数含有因子3,而总的培训人数1290也含有因子3,因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人,因此要使甲教室培训过的人数也含有3因子,则其举办次数必然含有3因子,因此只有C、D符合。将C选项代入,可知此时乙教室举办过15次培训,其总人数的尾数为5,而甲教室培训的总人数尾数总是为0,因此甲、乙教室的培训人数尾数为5,不符合要求。故正确答案为D。秒杀技由题意,甲教室每次培训50人,乙教室每次培训45,假设甲乙的次数分别为X、Y,则可得50X+45Y=1290,观察等式可知45Y的尾数必然为0,因此Y必然为偶数,从而X为奇数,仅D符合。故正确答案为D。
84、学校举办一次中国象棋比赛,有10名同学参加,比赛采用单循环赛制,每名同学都要与其他9名同学比赛一局。比赛规则,每局棋胜者得2分,负者得0分,平局两人各得1分。比赛结束后,10名同学的得分各不相同,已知:(1)比赛第一名与第二名都是一局都没有输过;(2)前两名的得分总和比第三名多20分;(3)第四名的得分与最后四名的得分和相等。那么,排名第五名的同学的得分是_____。
A: 8分B: 9分C: 10分D: 11分
参考答案: D 本题解释:正确答案是D考点统筹规划问题解析
85、大小两个数的和是50.886,较大数的小数点向左移动一位就等于较小的数,求较大的数是_____。
A: 46.25 B: 40.26 C: 46.15 D: 46.26
参考答案: D 本题解释:【解析】D。 四个选项的小数点后都是两位,两数之和为50.886,则两个数的尾数都为6,所以可以排除A、C两项。将B、D两项代入,只有D项符合。
86、已知鸡、兔头数之和为60,足数之和为200,问鸡兔相差多少只?_____
A: 10B: 15C: 20D: 25
参考答案: C 本题解释:参考答案:C题目详解:假设全为鸡,则:兔有: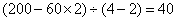 只,鸡有:
只,鸡有: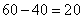 只,鸡兔相差:
只,鸡兔相差: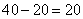 只。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>基本鸡兔同笼问题
只。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>基本鸡兔同笼问题
87、某班有120名学生,其中60%会说法语,余下的只会说英语。同时,会说法语的学生中有25%也会说英语,那么该班一共有多少学生会说英语?_____
A: 66B: 60C: 72D: 78
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题意易知,该班会说英语的学生人数为120×(1-60%)﹢120×60%×25%=66(人),故正确答案为A。
88、有一块草地,上面的青草每天都生长得一样快。这块草地上的青草供20头牛吃,可以吃12天,或者供25头牛吃,可以吃8天。某人有牛70头,如果要保证青草不被吃完,需要在几块这样的草地上放牧?_____
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:【答案】A。解析:假设这块草地原有草量为x,每天长草量为y,每头牛每天吃草的量为1,则根据公式可得: 解得x=10,这块草地每天的长草量够10头牛吃。要保证青草不被吃完,需要在70÷10=7(块)这样的草地上放牧。
解得x=10,这块草地每天的长草量够10头牛吃。要保证青草不被吃完,需要在70÷10=7(块)这样的草地上放牧。
89、小明、小刚和小红三人一起参加一次英语考试,已知考试共有100道题,且小明做对了68题,小刚做对了58题,小红做对了78题。问三人都做对的题目至少有几题?_____
A: 4题B: 8题C: 12题D: 16题
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析解析1:小明做错了100-68=32题,小刚做错了100-58=42题,小红做错了100-78=22题,要使”三人同时做对的题目最少”的情况是:三人做错的题都不一样。一共错了32+42+22=96题,还剩下100-96=4题至少三人都做对了,因此选A。解析2:共100题,小明对68题,小刚对58题,那么两人至少就有68+58-100=26题是同时对的,小红对78题,那么3人都做对的题目就至少有78+26-100=4,因此选A。
90、已知等式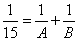 ,其中
,其中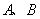 都是正整数,求
都是正整数,求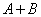 的最大值。_____
的最大值。_____
A: 341B: 287C: 256D: 230
参考答案: C 本题解释:参考答案:C题目详解: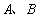 都是正整数:且
都是正整数:且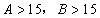 ;当
;当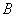 取最小值16时,
取最小值16时, 取最大值,此时
取最大值,此时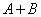 最大;
最大; ,由上式可得:
,由上式可得: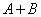 的最大值是
的最大值是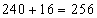 ;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
91、下图是由5个相同的小长方形拼成的大长方形,大长方形的周长是88厘米,问大长方形的面积是多少平方厘米?_____ 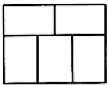
A: 472平方厘米B: 476平方厘米C: 480平方厘米D: 484平方厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析通过观察大长方形的上下两边,可见小长方形的长宽比为3:2,则设小长方形的长宽分别为3y、2y,根据题意得,3y×4+2y×5=88,解得y=4,因此大长方形长为:3y×2=24,宽为:3y+2y=20,则大长方形的面积为:24×20=480,故选择C选项。秒杀技由题意给出”5个相同的小长方形”,因此大长方形的面积是小长方形的5倍,由此可知面积应能被5整除,故答案为C。标签数字特性
92、某次考试100道选择题,每做对一题得1.5分,不做或做错一题扣1分,小李共得100分,那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:答案:A 解析:不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。
93、有一种长方形小纸板,长为19毫米,宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形,问最少要几块这样的小纸板拼合成一个正方形,问最少要几块这样的小纸板?_____
A: 157块B: 172块C: 209块D: 以上都不对
参考答案: C 本题解释:正确答案是C考点倍数约数问题解析拼成的正方形的边长必然是长方形的长和宽的公倍数,11和19的最小公倍数为11×19=209,故最少需要209个小纸板,正确答案为C。
94、甲,乙两个科室各有4名职员,且都是男女各半,现从两个科室中选出4人参加培训,要求女职员比重不得低于一半,且每个科室至少选1人,问有多少种不同的选法?_____
A: 67B: 63C: 53D: 51
参考答案: D 本题解释:参考答案 题目详解:第一种情况:4女。满足条件,有1种方法;第二种情况:3女一男。满足条件。有
题目详解:第一种情况:4女。满足条件,有1种方法;第二种情况:3女一男。满足条件。有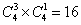 种方法;第三种情况:2女2男。减去都在同一个科室这一种情况。即
种方法;第三种情况:2女2男。减去都在同一个科室这一种情况。即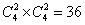 ;(其中扣去的为4个人都在第一个科室和都在第二科室)即
;(其中扣去的为4个人都在第一个科室和都在第二科室)即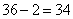 种方法;总共有
种方法;总共有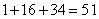 种。所以,选D。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
种。所以,选D。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
95、自然数  是一个两位数,它是一个质数,而且
是一个两位数,它是一个质数,而且 的个位数字与十位数字都是质数,这样的自然数有多少个?_____
的个位数字与十位数字都是质数,这样的自然数有多少个?_____
A: 4B: 6C: 8D: 12
参考答案: A 本题解释:参考答案:A题目详解:这样的数共有4个,23,37.53.73。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
96、甲、乙、丙三人买水果,甲买了3千克苹果和2千克梨,乙买了4千克苹果和3千克梨,丙买了3千克苹果和4千克梨。乙比甲多花7元,甲比丙少花5元。问甲、乙、丙共花了多少钱?_____。
A: 92.5元B: 112.5元C: 88.0元D: 67.5元
参考答案: D
97、以正方形的4个顶点和中心点中的任意三点为顶点可以构成几种面积不等的三角形?_____
A: 1B: 2C: 3D: 4
参考答案: B 本题解释:正确答案是B考点几何问题解析总共两类三角形:第一类是由正方形中心和相邻两个顶点构成,第二类是由正方形相邻三个顶点构成,因此可以构成2种面积不等的三角形,故正确答案为B。
98、地上放着一个每一面上都有一个数的六面体箱子,对面两个数的和均为27。甲能看到顶面和两个侧面,这三个面上的数字之和是35;乙能看到顶面和另外两个侧面,且这三个面上的数字和为47。箱子贴地一面的数字是:_____
A: 14B: 13C: 12D: 11
参考答案: B 本题解释:参考答案:B题目详解:先求出顶面的数字:甲、乙二人看到的数加起来一共为:2组对面加上2倍的顶面数字;则顶面的数字为:(35+47-27×2)÷2=14;根据对面两个数的和均为27:底面的数字为: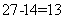 ;所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
;所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
99、一学校的750名学生或上历史课,或上算术课,或两门课都上。如果有489名学生上历史课,606名学生上算术课,问有多少学生两门课都上?_____。
A: 117B: 144C: 261D: 345
参考答案: D 本题解释:参考答案 题目详解:解法一:设两门课都上的学生有x人。
题目详解:解法一:设两门课都上的学生有x人。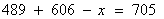
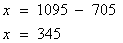 (原因:因为学数学的和学历史的人数和为1095人,但是全年级只有750人,这就说明有一部分同学是两科都学的,也就把两科都学的人算了两遍,所以只要减去年级总人数,剩下的就是两科都学的人数。)解法二:解设两门都上的人有
(原因:因为学数学的和学历史的人数和为1095人,但是全年级只有750人,这就说明有一部分同学是两科都学的,也就把两科都学的人算了两遍,所以只要减去年级总人数,剩下的就是两科都学的人数。)解法二:解设两门都上的人有 人,只学数学的人有
人,只学数学的人有 人,只学历史的人有
人,只学历史的人有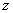 人。
人。 ①
①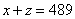 ②
②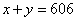 ③1-②得,
③1-②得,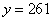 把
把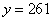 代入③中,得
代入③中,得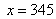 。所以,选D。解法三:直接用尾数法快解,秒杀题。
。所以,选D。解法三:直接用尾数法快解,秒杀题。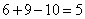 ,尾数为5的只有D。(该解析由用户“估计考不上”于2010-12-0213:04:48贡献,感谢感谢!)考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
,尾数为5的只有D。(该解析由用户“估计考不上”于2010-12-0213:04:48贡献,感谢感谢!)考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
100、A、B、C、D、E,5个小组开展扑克牌比赛,每两个小组之间都要比赛一场,到现在为止,A组已经比赛了4场,B组已经比赛了3场,C组已经比赛了2场,D组已经比赛了1场,问E组已经比赛了几场()
A: oB: 1C: 2D: 3
参考答案: C 本题解释:C【解析】A组已经比赛了4场,说明A组与B、C、D、E这4个组都进行过比赛;D组已经比赛了1场,则根据上一个条件,D组只与A组进行过比赛;B组已经比赛了3场,则根据上一个条件,B组只与A、C、E组进行过比赛;C组已经比赛了2场,则根据上面的条件,C组只能与A、B组进行过比赛;所以E组与A、B组进行过比赛。