浙江省2013年1月高等教育自学考试
高等数学(四)试题
课程代码:06604
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分
注意事项:
1. 答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2. 每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。不能答在试题卷上。
一、单项选择题(本大题共5小题,每小题2分,共10分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题纸”的相应代码涂黑。错涂、多涂或未涂均无分。
1.设函数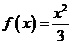 ,
,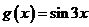 ,则复合函数f[g(x)]=
,则复合函数f[g(x)]=
A.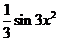 B.
B.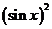
C.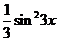 D.
D.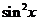
2.数列极限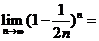
A.-2 B.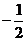
C.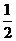 D.1
D.1
3.若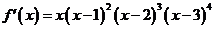 ,则f(x)的极值个数为
,则f(x)的极值个数为
A.1 B.2
C.3 D.4
4.函数lnx的原函数是
A.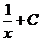 B.
B.
C.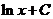 D.
D.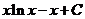
5.二元函数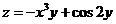 的全微分dz=
的全微分dz=
A.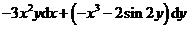 B.
B.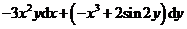
C.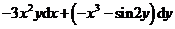 D.
D.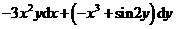
非选择题部分
注意事项:
用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
二、填空题(本大题共10小题,每小题3分,共30分)
6.函数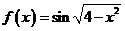 的定义域为______.
的定义域为______.
7.已知函数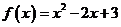 的单调增区间是[b,+∞),则b=______.
的单调增区间是[b,+∞),则b=______.
8.函数cos2x的最小正周期为______.
9.函数极限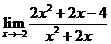 =______.
=______.
10.已知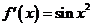 ,
,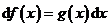 ,则g(x)=______.
,则g(x)=______.
11.曲线y=lnx在点(1,0)处的法线方程为y=ax+1,则a=______.
12.已知曲线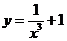 的铅直渐近线是x=b,则b=______.
的铅直渐近线是x=b,则b=______.
13.若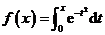 ,则f′(x)=______.
,则f′(x)=______.
14.若f(1)=2,f(3)=1,函数f′(x)连续,则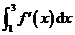 =______.
=______.
15.定积分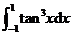 =______.
=______.
三、计算题(本大题共9小题,共52分)
(一)(每小题5分,共20分)
16.已知函数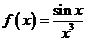 ,求f′(x)和f′(1).
,求f′(x)和f′(1).
17.求不定积分 .
.
18.求定积分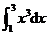 .
.
19.求定积分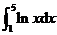 .
.
(二)(每小题6分,共18分)
20.设隐函数y=y(x)由方程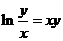 确定,求y′.
确定,求y′.
21.求极限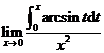 .
.
22.求二元函数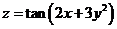 的一阶偏导数.
的一阶偏导数.
(三)(每小题7分,共14分)
23.求极限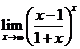 .
.
24.求不定积分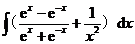 .
.
四、应用题(本大题8分)
25.求由曲线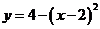 与直线y=x所围成的平面图形的面积.
与直线y=x所围成的平面图形的面积.