微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、公路上有三辆同向行驶的汽车,其中甲车的时速为63公里,乙、丙两车的时速均为60公里,但由于水箱故障,丙车每连续行驶30分钟后必须停车2分钟。早上10点,三车到达同一位置,问1小时后,甲、丙两车最多相距多少公里?_____
A: 5B: 7C: 9D: 11
参考答案: B 本题解释:正确答案是B考点行程问题解析在这1个小时中,丙车最多休息4分钟,也即丙在一个小时内最少行程为60×56÷60=56公里。而甲车持续行驶,可达63公里。因此两车最多相距7公里,故正确答案为B。
2、甲、乙两个厂生产同一种玩具,甲厂生产的玩具数量每个月保持不变,乙厂生产的玩具数量每个月增加一倍,已知一月份甲、乙两个厂生产的玩具总数是98件,二月份甲、乙两个厂生产的玩具总数是106件。那么乙厂生产的玩具数量第一次超过甲厂生产的玩具数量是在几月份?_____
A: 3月B: 4月C: 5月D: 7月
参考答案: C 本题解释:正确答案是C考点不等式分析问题解析
3、_____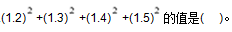
A: 6.30B: 6.49C: 7.56D: 7.34
参考答案: D 本题解释:正确答案是D考点计算问题解析计算原式尾数,4+9+6+5=24,末位为4,故正确答案为D。标签尾数法
4、甲、乙、丙三人,甲每分钟走50米,乙每分钟走40米,丙每分钟走35米,甲、乙从A地,丙从B地同时出发,相向而行,丙遇到甲2分钟后遇到乙,那么,A、B两地相距多少米?_____
A: 250米B: 500米C: 750米D: 1275米
参考答案: D 本题解释:正确答案是D考点行程问题解析设AB两地相距s米,丙遇到乙的时间为t,则丙遇到甲的时间为(t+2),由题意知s=(50+35)t,s=(40+35)(t+2),解得s=1275,故正确答案为D。公式:相遇问题,相遇距离=(大速度+小速度)×相遇时间。秒杀技甲、乙从A地,丙从B地同时出发,相向而行,所以甲丙相对速度为50+35=85米/分钟,乙丙相对速度为40+35=75米/分钟,所以AB两地距离能整除85和75,只有D项1275符合要求,故正确答案为D。标签数字特性公式应用
5、某企业响应国家发展低碳经济的号召,比去年节约了10%的成本,在收入不变的情况下使得企业的利润提高了30%,则今年的成本占收入的比例为_____。
A: 65%B: 67.5%C: 75%D: 80%
参考答案: B 本题解释:【答案】B。解析:显然去年的成本的10%等于去年利润的30%,因此去年成本占收入的比例为3÷(3+1)×100%=75%,今年的成本下降了10%,而收入不变,因此其所占比例也下降了10%,因此今年所占比例为75%×(1—10%)=67.5%,因此选B。
6、_____ 
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点几何问题解析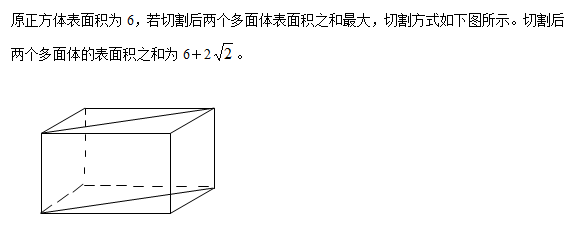
7、有面值为8分、1角和2角的三种纪念邮票若干张,总价值为1元2角2分,则邮票至少有_____。
A: 7张B: 8张C: 9张D: 10张
参考答案: C 本题解释:C【解析】要使邮票最少,则要尽量多的使用大面额邮票,所以要达到总价值,2角的邮票要使用4张,1角的邮票要使用1张,8分的邮票要4张,这样使总价值正好为1元2角2分,所以要用9张。
8、爸爸、哥哥、妹妹三人现在的年龄和是64岁,当爸爸的年龄是哥哥年龄的3倍时,妹妹是9岁。当哥哥的年龄是妹妹年龄的2倍时,爸爸是34岁,现在三人的年龄各是多少岁?_____
A: 10,14,40B: 6,18,40C: 8,14,42D: 9,15,40
参考答案: A 本题解释:参考答案:A题目详解:解法一:设妹妹与哥哥年龄差为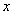 ,哥哥与爸爸年龄差为
,哥哥与爸爸年龄差为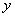 。当爸爸的年龄是哥哥年龄3倍的时候哥哥的年龄相当于
。当爸爸的年龄是哥哥年龄3倍的时候哥哥的年龄相当于 ,此时
,此时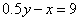 。当哥哥年龄是妹妹年龄2倍时,即
。当哥哥年龄是妹妹年龄2倍时,即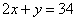 。联立这两个方程得到
。联立这两个方程得到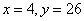 。妹妹今年年龄为:(64-26-4-4)÷3=10岁,哥哥今年年龄为:14岁,爸爸今年年龄为:40岁。所以,选A。解法二:代入法,A正确,所以,选A考查点:数量关系>数学运算>特殊情境问题>年龄问题
。妹妹今年年龄为:(64-26-4-4)÷3=10岁,哥哥今年年龄为:14岁,爸爸今年年龄为:40岁。所以,选A。解法二:代入法,A正确,所以,选A考查点:数量关系>数学运算>特殊情境问题>年龄问题
9、 _____
_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:正确答案是C考点计算问题解析
10、小明通常总是步行上学,有一天他想锻炼身体,前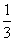 路程快跑,速度是步行速度的4倍,后一段的路程慢跑。速度是步行速度的2倍。这样小明比平时早35分钟到校,小明步行上学需要多少分钟?_____
路程快跑,速度是步行速度的4倍,后一段的路程慢跑。速度是步行速度的2倍。这样小明比平时早35分钟到校,小明步行上学需要多少分钟?_____
A: 60B: 45C: 120D: 90
参考答案: A 本题解释:参考答案:A题目详解:设路程是 ,步行速度是
,步行速度是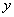 :小明步行上学需要
:小明步行上学需要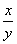 分钟;根据题意,列等式得:
分钟;根据题意,列等式得: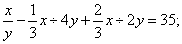 得到
得到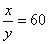 。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
11、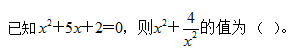 _____
_____
A: 21B: 23C: 25D: 29
参考答案: A 本题解释:正确答案是A解析 考点计算问题
考点计算问题
12、甲、乙、丙三队要完成A,B两项工程,B工程工作量比A工程的工作量多1/4 ,甲、乙、丙三队单独完成A工程所需时间分别是20天、24天、30天。为了同时完成这两项工程,先派甲队做A工程,乙、丙两队共同做B工程,经过几天后,又调丙队与甲队共同完成A工程,那么,丙队甲队合做了多少天? _____
A: 18B: 15C: 10D: 3
参考答案: D 本题解释:【解析】D。解析:三队完成这项工程一共用了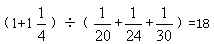 天,乙队一直在做B工程,一共做了
天,乙队一直在做B工程,一共做了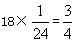 ,则B工程剩下的
,则B工程剩下的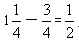 为丙做的,故丙队与乙队合做了
为丙做的,故丙队与乙队合做了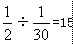 天,与甲队合做了18-15=3天。
天,与甲队合做了18-15=3天。
13、小张和小王同时骑摩托车从A地向B地出发,小张的车速是每小时40公里,小王的车速是每小时48公里。小王到达B地后立即向回返,又骑了15分钟后与小张相遇。那么A地与B地之间的距离是多少公里?_____
A: 144B: 136C: 132D: 128
参考答案: C 本题解释:C。相遇的时候小王比小张多走了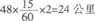 ,共用时24÷(48-40)=3小时,所以A地与B地之间的距离为48×3-12=132公里。
,共用时24÷(48-40)=3小时,所以A地与B地之间的距离为48×3-12=132公里。
14、 _____
_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点其他解析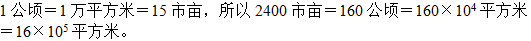 故正确答案为D。
故正确答案为D。
15、423×187-423×24-423×63的值是_____。
A: 41877B: 42300C: 42323D: 42703
参考答案: B 本题解释: B 【解析】原式可化为423×(187-24-63)。
16、某市气象局观测发现,今年第一、二季度本市降水量分别比去年同期增加了11%和9%,而两个季度降水量的绝对增量刚好相同。那么今年上半年该市降水量同比增长多少?_____
A: 9.5%B: 10%C: 9.9%D: 10.5%
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:设绝对增长量是X,则今年上半年的增长量是2X,去年的降水量是X/11%+X/9%,同比增长=2X/(X/11%+X/9%)=9.9%,故正确答案为C。解析2: 标签十字交叉法
标签十字交叉法
17、_____
A: 2cmB: 3cmC: 3.5cmD: 4cm
参考答案: A 本题解释:正确答案是A解析几何问题标签勾股定理
18、把自然数1,2,3,4,5,……,98,99分成三组,如果每组数的平均数刚好相等,那么此平均数为_____。
A: 55B: 60C: 45D: 50
参考答案: D 本题解释:正确答案是D考点数列问题解析每组平均数相等,那么这个数就是全体的平均数,而平均数即为中位数,且相等于首项与末项之和的一半,口算知为50。故正确答案为D。标签整体考虑
19、要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要多少分钟完成?_____
A: 10B: 15C: 16D: 18
参考答案: D 本题解释:答案:D【解析】此题实质上是一道工程问题。设纸飞机总量为1,则甲甲每分钟完成1/30,乙每分钟完成1/45,甲乙共花时间为1/(1/30+1/45)=18。故正确答案应为选项D。
20、甲、乙、丙三人共做了183道数学题,乙做的题比丙的2倍少4题,甲做的题比丙的3倍多7题,求甲做的题比乙多多少?_____
A: 67B: 41C: 26D: 30
参考答案: B 本题解释:B【解析】设丙共做x题,则甲做了(3x+7)题,乙做了(2x-4)题,由题意可得:x+(3x+7)+(2x-4)=183,x=30。故甲做了97题,乙做了56题,所以甲比乙多做97-56=41(题)。
21、_____ 
A: AB: BC: CD: D
参考答案: B 本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等,又因为正三角形和正六边形的边长的个数比是1:2,所以其边长之比为2:1,假设正三角形的边长为2,则正六边形的边长为1。正六边形可以分成6个小正三角形,如下图所示,边长为1的小正三角形面积:加长为2的正三角形面积=1:4。所以正六边形面积:正三角形面积=6:4=1.5,故正确答案为B。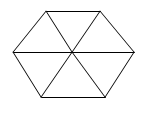 标签赋值思想
标签赋值思想
22、某单位职工24人中,有女性11人,已婚的16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人? _____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: 【答案】B。解析:易知该单位有男性13人,其中已婚的有10人,故未婚的有3人,选B。
23、某人同时购买2年期、5年期和10年期三种国债,投资额的比为5:3:2。后又以与前次相同的投资总额全部购买5年期国债,则此人两次对5年期国债的投资额占两次总投资的比例的_____。
A: 3/5B: 7/10C: 3/4D: 13/20
参考答案: D
24、(2008山西)若干学校联合进行团体表演,参演学生组成一个方阵,已知方阵由外到内第二层有104人,则该方阵共有学生_____人。
A: 625B: 841C: 1024D: 1369
参考答案: B 本题解释:参考答案:B题目详解:根据方阵公式:最外层人数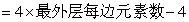 可得:由外到内第二层每排的学生数:
可得:由外到内第二层每排的学生数: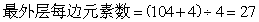 个;最外一层每排有学生有:最外层每边元素数=内层每边元素数+2:
个;最外一层每排有学生有:最外层每边元素数=内层每边元素数+2: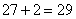 个;所以该方阵共有学生有:
个;所以该方阵共有学生有: 个。所以,选B考查点:数量关系>数学运算>特殊情境问题>方阵问题>实心方阵问题
个。所以,选B考查点:数量关系>数学运算>特殊情境问题>方阵问题>实心方阵问题
25、有300名求职者参加高端人才专场招聘会,其中软件设计类、市场营销类、财务管理类和人力资源管理类分别有100、80、70和50人。问至少有多少人找到工作,才能保证一定有70名找到工作的人专业相同?_____
A: 71B: 119C: 258D: 277
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析考虑对这些人进行分配,在使得每个专业人数不足70的情况下尽可能的增加就业人数,则四类专业可就业的人数分别为69、69、69、50,总和为257人。此时再多1人,则必然有一个专业达到70人,因此所求最少人数为258人,故正确答案为C。标签构造调整
26、有两种溶液,甲溶液中蛋清的浓度为20%,蜂蜜的浓度为15%,乙溶液中蛋清的浓度为50%,蜂蜜的浓度为20%,现在有甲溶液2千克,要将一定量的乙溶液与甲溶液混合,混合后所得溶液的蛋清浓度是蜂蜜浓度的2倍,问需要多少千克的乙溶液?_____
A: 2B: 1.5C: 1D: 0.5
参考答案: A 本题解释:A。
27、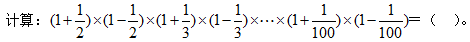 _____
_____
A: 101/100B: 101/200C: 101/300D: 201/400
参考答案: B 本题解释:正确答案是B考点计算问题解析 故正确答案为B。
故正确答案为B。
28、某医院有一氧气罐匀速漏气,该氧气罐充满后同时供40人吸氧,60分钟后氧气耗尽,再次充满该氧气罐同时供60个人吸氧,则45分钟后氧气耗尽。问如果该氧气罐充满后无人吸氧,氧气耗尽需要多长时间?_____
A: 1.5小时B: 2小时C: 2.5小时D: 3小时
参考答案: D 本题解释:正确答案是D考点牛吃草问题解析这是一个变形的牛吃草问题。设原有氧气为M,漏气速度为V,则可得(40+V)×60=(60+V)×45=M,解得V=20,M=3600,如果没人吸氧,则可得耗尽的时间为3600÷20=180分钟,即3小时。故正确答案为D。
29、建造一个容积为16立方米,深为4米的立方体无盖水池,如果池底和池壁的造价分别为每平方米160元和每平方米100元,那么该水池的最低造价是多少元?_____
A: 3980B: 3560C: 3270D: 3840
参考答案: D 本题解释:正确答案是D考点函数最值问题解析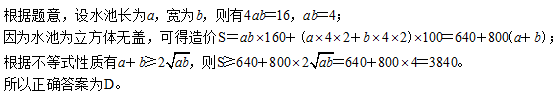 标签公式应用
标签公式应用
30、某项射击资格赛后的表明,某国四名运动员中,三名运动员的平均环数加上另一运动员的环数,计算后得到的环数分别为92、114、138、160,则此国四名运动员资格赛的平均环数是_____。
A: 63B: 126C: 168D: 252
参考答案: A 本题解释:正确答案是A考点平均数问题解析四名运动员的平均环数必然小于任意三名运动员环数加上另一名的环数。选项中只有A<92,符合条件。故正确答案为A。
31、如右图所示,正方形ABCD的边长为5cm,AC、BD分别是以点D和点C为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小_____。(π取3.14)
参考答案: B
32、一堆沙重480吨,用5辆载重相同的汽车运3次,完成了运输任务的25%,余下的沙由9辆同样的汽车来运,几次可以运完?_____
A: 4次B: 5次C: 6次D: 7次
参考答案: B 本题解释:【答案】B。解析:因为用5辆载重相同的汽车运3次,完成了运输任务的25%,所以每辆车一次可以运总工程量的(25÷5÷3)%=(5/3)%,所以9辆车一次可以运总工程量的9×(5/3)%=15%,余下的75%用9辆车运的话需要75÷15=5次,故正确答案为B。
33、某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道联接建筑物内最远两点,预设的最短管道长度介于_____。
A: 70—80米之间B: 60—70米之间C: 90—100米之间D: 80—90米之间
参考答案: D 本题解释:正确答案是D考点几何问题解析
34、一个游泳池,甲管注满水需6小时,甲、乙两管同时注水,注满要4小时。如果只用乙管注水,那么注满水需_____小时。
A: 14B: 12C: 10D: 8
参考答案: B 本题解释:正确答案是B考点工程问题解析解析1:该题为工程问题,直接赋值求解,甲单独完成注水,时间为6小时,甲和乙共同注水时间是4小时,取最小公倍数为12作为总工程量。则甲和乙一起注水4小时,甲完成的工作量12×4/6=8,乙完成的工作量为12-8=4份,乙每小时完成1份工作量,单独注水需要12个小时完成12份工作量。故正确答案为B。解析2:该问题为工程问题,可以比例转化求解。赋值工程量为6,甲单独注水时间为6,甲乙同注水4小时,甲完成的工程量是6×4/6=4,则乙完成的工程量是6-4=2,则甲乙效率比为2:1,单独注水时间比为1:2。则乙单独注水需要12小时。标签比例转化
35、某班级去超市采购体育用品时发现买4个篮球和2个排球共需560元,而买2个排球和4个足球则共需500元。问如果篮球、排球和足球各买1个,共需多少元?_____
A: 250元B: 255元C: 260元D: 265元
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析将两次购买合并,4个篮球、2个排球和2个排球、4个足球刚好能组成4个篮球、4个排球、4个足球,共计560+500=1060元,因此篮球、排球、足球各买一个需要1060÷4=265元,故正确答案为D。标签整体考虑
36、有四个数,其中每三个数的和分别是45,46,49,52,那么这四个数中最小的一个数是多少?_____
A: 12B: 18C: 36D: 45
参考答案: A 本题解释:将45,46,49,52直接相加,可知其值等于原来四个数之和的3倍,于是可知原四个数字之和为(45+46+49+52)÷3=64,因此最小的数为64-52=12。故选A。
37、从1到500的所有自然数中,不含有数字4的自然数有多少个?_____
A: 323B: 324C: 325D: 326
参考答案: B 本题解释:参考答案:B题目详解:把一位数看成是前面有两个0的三位数:如:把1看成是001;把两位数看成是前面有一个0的三位数:如:把11看成011;那么所有的从1到500的自然数都可以看成是“三位数”。除去500外,考虑不含有4的这样的“三位数”:百位上,有0、1、2、3这四种选法;十位上,有0、1、2、3、5、6、7、8、9这九种选法;个位上,有0、1、2、3、5、6、7、8、9,也是有九种选法.所以,除500外,有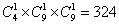 个不含4的“三位数”。注意到:这里面有一个数是000,应该去掉;而500还没有算进去,应该加进去;所以,从1到500中,不含4的自然数有324-1+1=324个。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的排列与位数关系
个不含4的“三位数”。注意到:这里面有一个数是000,应该去掉;而500还没有算进去,应该加进去;所以,从1到500中,不含4的自然数有324-1+1=324个。所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的排列与位数关系
38、一单位组织员工乘坐旅游车去泰山,要求每辆车上的员工人数相等。起初,每辆车上乘坐22人,结果有1人无法上车;如果开走一辆空车,那么所有的游客正好能平均乘到其余各辆旅游车上,已知每辆车上最多能乘坐32人。请问该单位共有多少员工去了泰山?_____
A: 269B: 352C: 478D: 529
参考答案: D 本题解释:D。开走一辆空车,则剩余22+1=23人,需要把23人平均分配到剩余的旅游车上。23的约数只有23和1,而每辆车最多能乘坐32人,排除将23人分配到1辆车上的情况(22+23>32),只能每辆车上分配1人,分配后每辆车有22+1=23人。进行条件转换,如果没有开走那辆车,那么每辆车分配23人,还少23人,加上已有条件“每辆车上乘坐22人,结果有1人无法上车”,就转化成了常规的盈亏问题。有车(1+23)÷(23-22)=24辆。有员工24×22+1=529人。
39、一次数学考试共有20道题,规定:答对一题得2分,答错一题扣1分,未答的题不计分。考试结束后,小明共得23分,他想知道自己做错了几道题,但只记得未答的题的数目是个偶数。请你帮助小明计算一下,他答错了多少道题_____
A: 3B: 4C: 5D: 6
参考答案: A 本题解释:【答案】A,代入即可,答对13道题,得26分,打错3道扣3分,未答的题的数目是4道恰好是个偶数。
40、一艘游轮逆流而行,从A地到B地需6天;顺流而行,从B地到A地需4天。问若不考虑其他因素,一块塑料漂浮物从B地漂流到A地需要多少天?_____
A: 12天B: 16天C: 18天D: 24天
参考答案: D 本题解释:正确答案是D解析设两地距离为12,则逆流速度=12÷6=2,顺流速度=12÷4=3,顺流速度-水流速度=逆流速度+水流速度,则水流速度=0.5,所以漂流时间=12÷0.5=24天,故正确答案为D。行程问题标签顺水漂流模型赋值思想
41、现有篮球、排球、乒乓球、足球、网球五门选修课,每名学生必须要从中选出而且仅选择2门选修课,问至少有多少名学生进行选课,才能保证至少有6名学生所选的选修课相同?_____
A: 48B: 50C: 51D: 70
参考答案: C 本题解释:【答案】C。解析:要求五门课程选出两门,共有C25=10种,要至少有6名学生所选的选修课相同,那么这10中选课方式各有5名学生选择,共有10×5=50人,之后再来一人,就可以保证有6名学生所选的选修课相同,则为50+1=51人,所以答案为C。
42、某项工程,甲单独完成需要8天,乙需要4天,甲做一半换乙,乙做剩余一半又换甲,甲又做剩余一半再换乙完成。问整个工程花费_____天。
A: 5.5 B: 6 C: 6.5 D: 7
参考答案: C 本题解释:C。假设工作总量为8,则甲每天完成1,乙每天完成2,甲先完成一半需要4÷1=4天,乙完成剩下一半需要2÷2=1,甲又做剩余一半需要1÷1=1天,剩下乙完成需要1÷2=0.5天,因此共需要6.5天。
43、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。
44、某商品76件,出售给33位顾客,每位顾客最多买3件。买1件按原定价,买2件降价10%,买3件降价20%。最后结算,平均每件恰好按原价的85%出售,那么买3件的顾客有多少人?_____
A: 14B: 10C: 7D: 2
参考答案: A 本题解释:A【解析】 买2件商品按原价的90%,买3件商品按原价的80%。由于 =85%,即1个人买1件与1个人买3件的平均,每件正好是原定价的85%;又由于 =85%,所以2个人买3件与3个人买2件的平均,每件正好是原价的85%。因此,买3件的人数是买1件的人数与买2件人数的之和。设买2件的有x人,则买1件的有(33-x- x)÷2(人),买3件的有 x+(33-x- x)÷2(人)。因为共有商品76件,于是有方程(33-x- x)÷2+2x+3×[ x+(33-x- x)÷2]=76,解出x=15(人)。买3件的有x+(33-x- x)÷=14(人)故买3件的顾客有14人。选A。
45、袋子里装有红、蓝两色的小球各12个,先从袋子中拿出一个球,然后将它放回袋子中,混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有_____。
A: 20%B: 25%C: 50%D: 60%
参考答案: C 本题解释:【解析】因为两种颜色的小球数量相等,那么每次抽中其中一种颜色小球的概率均为50%。第一种情况:第一次抽中了红色小球,第二次抽中了蓝色小球,概率是50%×50%一25%;第二种情况:第一次抽中了蓝色小球,第二次抽中了红色小球,概率是50%×50%=25%。那么两次抽中不同颜色的小球的整体概率等于两种情况下的概率之和,即25%+25%=50%,答案为C。
46、
A: 2.75B: 3.25C: 2D: 3
参考答案: 本题解释:参考答案:C题目详解:由两点之间线段最短可知:连接AB,交公路L于点E,E点就是A、B两个村庄到此处处理垃圾都比较方便的地方。设CE距离为x:根据tanA=a/b可得:tanA=x/1=x,tanB=(6-x)/2=3-x/2;由于∠A=∠B:故x=3-x/2,解得,x=2。即应建在离C处2公里。所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>与线、角相关问题(平面)
47、王方将5万元存入银行,银行利息为1.5%/年,请问2年后,它的利息是多少?_____
A: 1500元B: 1510元C: 1511元D: 1521元
参考答案: C 本题解释:正确答案是C考点经济利润问题解析根据题意两年后利息为50000×(1+0.015)×(1+0.015)-50000=2×50000×0.015+50000×0.015×0.015=1511.25,故正确答案为C。
48、某商场开展购物优惠活动:一次购买300元及以下的商品九折优惠;一次购买超过300元的商品,其中300元九折优惠,超过300元的部分八折优惠。小王购物第一次付款144元,第二次又付款310元。如果他―次购买并付款,可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:A【解析】统筹优化问题。由题意,第一次付款144元可得商品原价为160元;第二次付款为310元,可得原价为350元。故总价510元,按照优惠,需付款300×0.9+210×0.8=438元,节省了454-438=16元。
49、(2008北京应届,第16题)某单位今年新进3个工作人员,可以分配到3个部门,但是每个部门至多只能接收2个人,问共有几种不同的分配方案_____。
A: 12B: 16C: 24D: 以上都不对
参考答案: C 本题解释:参考答案:C题目详解:总体分为两种情形:1.如果三个部门每个部门分配一个工作人员:共有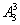 ;种分配方案;二.如果三个部门分别分配0、1、2个工作人员:一共有:
;种分配方案;二.如果三个部门分别分配0、1、2个工作人员:一共有: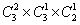 种分配方案;综上,总的分配方案为:
种分配方案;综上,总的分配方案为: ;所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
;所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
50、某市居民生活用电每月标准用电量的基本价格为每度0.50元,若每月用电量超过标准用电量,超出部分按其基本价格的80%收费,某户九月份用电84度,共交电费39.6元,则该市每月标准用电量为_____。
A: 60度B: 65度C: 70度D: 75度
参考答案: A 本题解释:【答案解析】基本价格的80%是0.5×0.8=0.4,设每月标准用电X度,则0.5X+(84-X)×0.4=39.6,解得X=60,选A。
51、在1至100这100个数中,有既不能被5整除也不能被9整除的数,它们的和是_____。
A: 1644B: 1779C: 3406D: 3541
参考答案: D 本题解释:【答案解析】先求出被5或9整除的数的和。1至100中被5整除的数有5,10,15,…,100,和为5+10+15+…+100=(100+5)×20÷2=10501至100中被9整除的数有9,18,…,99,和为9+18+27+…+99=(9+99)×11÷2=594又因为1~100中,45,90这两个数同时被5与9整除,于是所求的和是(1+2+…+100)-(5+10+…+100)-(9+18+…+99)+(45+90)=3541。因此,本题正确答案为D。
52、 _____
_____
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点年龄问题解析y表示丙当年的年龄,10年前丙为y-10岁,10年前甲为(y-10)/2=y/2-5岁,5年前甲为y/2岁,5年前乙的年龄为(y/2)/3=y/6岁,则乙当前年龄为y/6+5岁。故正确答案为A。
53、某船第一次顺流航行21千米又逆流航行4千米,第二次在同一河道中顺流航行12千米,逆流航行7千米,结果两次所用的时间相等。则顺水船速与逆水船速之比是_____。(设船本身的速度及水流的速度都是不变的)
A: 4∶1B: 3∶1C: 2∶1D: 9∶1
参考答案: B 本题解释:B 【解析】船第一次顺流航行21千米,第二次顺流航行12千米,21-12=9,也就是第一次顺流多用了航行9千米所用的时间,第二次逆流比第一次多用时间于3千米的航行上,总的两次时间相等。就是顺流9千米用的时间等于逆流3千米所用的时间。顺流船速:逆流船速=(21-12)∶(7-4)=3∶1,即顺水船速是逆水船速的3倍。
54、一杯糖水,第一次加入一定量的水后,糖水的含糖百分比变为15%;第二次又加入同样多的水,糖水的含糖百分变比为12%;第三次再加入同样多的水,糖水的含糖百分比将变为多少?_____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:【答案】C。解析:设第一次加水后糖水总量为100,糖为100×15%=15,则第二次加水后糖水变为15÷12%=125,所以每次加入的水为125-100=25,故第三次加水后糖水的含糖百分比为15÷(125+25)=10%。
55、把长为60cm的铁丝围成矩形,则矩形最大面积为:_____
A: 15B: 60C: 225D: 450
参考答案: C 本题解释:参考答案:C题目详解:设矩形的长为xcm,宽为(30-x)cm:则矩形的面积S=x(30-x)=30x-x2;对面积求导得: =30-2x,令
=30-2x,令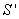 =0时,
=0时,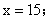 即当长和宽均为15cm时;矩形的最大面积
即当长和宽均为15cm时;矩形的最大面积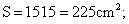 所以,选C;考查点:数量关系>数学运算>计算问题之算式计算>最值问题
所以,选C;考查点:数量关系>数学运算>计算问题之算式计算>最值问题
56、有浓度为4%的盐水若干克,蒸发了一些水分后浓度变成l0%,再加入300克4%的盐水后,变为浓度6.4%的盐水,则最初的盐水是_____
A: 200克B: 300克C: 400克D: 500克
参考答案: D 本题解释: 【解析】D。可以采用带入法,将选项代入题干中,发现只有当最初的盐水是500克的时候才能满足要求,或者利用倒推方法解题。
57、某住户安装了分时电表,白天电价0.55元,夜间电价是0.3元。计划是7月份用电400度,电费不超过160元,那么白天用电不超过多少度?_____
A: 150B: 160C: 170D: 180
参考答案: B 本题解释:参考答案:B题目详解:设白天用电x度:则有0.55x+(400-x)×0.3≤160,解得x≤160。所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
58、一个人到书店购买了一本书和一本杂志,在付钱时,他把书的定价中的个位上的数字和十位上的看反了,准备付21元取货。售货员说∶“您应该付39元才对。”请问书比杂志贵多少钱?_____
A: 20B: 21C: 23 0D: 24
参考答案: C 本题解释:【答案】C。解析:数字看反前后,书价相差18,说明十位和个位数字相差为2,总价为39,故书价只能是31,则杂志的价格是8.相差23。
59、筑路队原计划每天筑路720米,实际每天比原计划多筑路80米,这样在规定完成全路修筑任务的前3天,就只剩下1160米未筑,这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释:【解析】:现在每天筑路:720+80=800(米)规定时间内,多筑的路是:(720+80)×3-1160=2400-1160=1240(米)求出规定的时间是1240÷80=15.5(天),这条路的全长是,720×15.5=11160(米)。故本题选C。
60、某班有120名学生,其中60%会说法语,余下的只会说英语。同时,会说法语的学生中有25%也会说英语,那么该班一共有多少学生会说英语?_____
A: 66B: 60C: 72D: 78
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题意易知,该班会说英语的学生人数为120×(1-60%)﹢120×60%×25%=66(人),故正确答案为A。
61、已知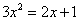 ,则
,则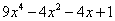 =_____ B: 1C: 2D: 4
=_____ B: 1C: 2D: 4
参考答案: C 本题解释:参考答案:C题目详解:根据题干中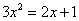 ,可得
,可得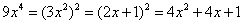 ,那么:
,那么: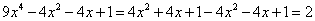 。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
62、规定两人轮流做一个工程,要求第一个人先做1个小时,第二个人接着做1个小时,然后再由第一个人做1个小时,然后又由第二个人做1个小时,如此反复,做完为止。如果甲、乙轮流做一个工程需要9.8小时,而乙、甲轮流做同样的工程只需要9.6小时,那乙单独做这个工程需要多少小时? _____
A: 6.4B: 7.3C: 8.2D: 9.7
参考答案: B 本题解释:【答案】B。解析:把整个工程看做一个过程,甲乙轮流顺序不一样导致时间不一样,而前面8小时中,两次循环完成的工程是一样的,因此考虑8小时之后的两人的工作效率差。即甲工作2小时相当于乙工作1小时。第一次甲一共做了5小时,换做乙只用2.5小时,即总时间可以节省2.5小时,所以乙单独做只用9.8-2.5=7.3小时。
63、2004×(2.3×47+2.4)÷(2.4×47-2.3)的值为_____。
A: 2003B: 2004C: 2005D: 2006
参考答案: B 本题解释:正确答案是B考点计算问题解析原式=2004×(2.3×47+2.4)÷[(2.3+0.1)×47-2.3]=2004×(2.3×47+2.4)÷(2.3×47+4.7-2.3)=2004×(2.3×47+2.4)÷(2.3×47+2.4)=2004。因此正确答案为B。
64、光的速度是每秒30万千米,太阳离地球1亿5千万千米。问:光从太阳到地球要用几分钟?_____
A: 83B: 12C: 7.2D: 20
参考答案: A 本题解释:【答案】A。解析:150000000÷300000÷60=150÷3÷6=50÷6=8.3(分)。故应选择A。
65、甲、乙、丙三辆车的时速分别为60公里、50公里和40公里,甲从A地,乙和丙从B地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙,问A、B两地相距多少公里?_____
A: 150公里B: 250公里C: 275公里D: 325公里
参考答案: C 本题解释:正确答案是C考点行程问题解析解析1:甲乙相遇时,甲走了全程的60÷(50+60)=6/11;甲丙相遇时,甲走了全程的60÷(40+60)=6/10;在甲乙相遇之后到甲丙相遇,甲走了全程的6/10-6/11=3/55,这段路程为60×15/60=15(公里),所以AB相距15÷(3/55)=275(公里)。解析2:设AB相距s公里,则s/(60+50)=s/(60+40)-1/4,解得s=275(公里)。故正确答案为C。
66、一个数能被3、5、7整除,若用11去除这个数则余1,这个数最小是多少?_____
A: 105B: 210C: 265D: 375
参考答案: B 本题解释:B。这个数能被3、5、7整除,因此这个数是105的倍数.若这个数是105,105除以11的余数是6,不符合题意;若这个数是105×2=210,210除以11的余数是1,满足题意。因此这个数最小是210。
67、当含盐为30%的60克盐水蒸发为含盐40%的盐水时,盐水重量是多少克?_____
A: 45B: 50C: 55D: 60
参考答案: A 本题解释:正确答案是A考点浓度问题解析本题关键点在于溶质质量不变,仍为60×30%=18克,则浓度为40%时盐水重量为18÷40%=45克,故正确答案为A。
68、如右图所示,△ABC是等腰直角三角形,AB=12,AD的长度是CD的2倍,四边形EBCD与△AED的面积之比为3:2,AE的长度是_____。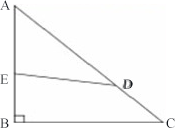
A: 6.9B: 7.1C: 7.2D: 7.4
参考答案: C 本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3:2,则三角形ABC与三角形AED的面积之比为5:2。已知AD的长度是CD的2倍,则AD的长度是AC的2/3。作DF垂直AB于点F,则DF=2/3BC(相似三角形原理),三角形ABC的面积=1/2×AB×BC,三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式,可得AE=3/5AB=36/5=7.2。所以正确答案为C。
69、一列客车长250米,一列货车长350米,在平行的轨道上相向行驶,从两车头相遇到两车尾相离经过15秒,已知客车与货车的速度比是5:3。问两车的速度相差多少?_____
A: 10米/秒B: 15米/秒C: 25米/秒D: 30米/秒
参考答案: A 本题解释:正确答案是A考点行程问题解析两车头相遇到两车尾相离相当于两车车尾相遇过程,设两车速度为5v、3v,则有15×(5v+3v)=250+350,解得v=5,因此两车速度相差5v-3v=2v=10米/秒。标签赋值思想比例转化
70、爷爷的老式时钟的时针与分针每隔66分重合一次。如果早晨8点将时钟对准,到第二天早晨时钟再次指示8点时,实际是几点几分?_____
A: 8点8分B: 8点10分C: 8点12分D: 8点16分
参考答案: C 本题解释:参考答案:C题目详解:对于标准钟表:时针与分针每重合一次需要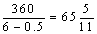 分;则老式时钟每重合一次比标准时间慢
分;则老式时钟每重合一次比标准时间慢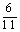 分;从12点开始的24时。分针转24圈,时针转2圈,分针比时针多转22圈,即22次追上时针;也就是说24时正好重合22次:所以老式时钟的时针与分针共重合了22次;所以比标准时间慢:
分;从12点开始的24时。分针转24圈,时针转2圈,分针比时针多转22圈,即22次追上时针;也就是说24时正好重合22次:所以老式时钟的时针与分针共重合了22次;所以比标准时间慢: 分;故实际时间为8点12分。所以,选C。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时钟的校准问题
分;故实际时间为8点12分。所以,选C。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时钟的校准问题
71、某铁路线上有25个大小车站,那么应该为这条路线准备多少种不同的车票?_____
A: 500B: 600C: 400D: 450
参考答案: B 本题解释:【解析】B。25×24=600
72、1-2+3-4+5-6+7-8+…+1989-1990+1991=_____
A: 895B: 896C: 995D: 996
参考答案: D 本题解释:正确答案是D考点计算问题解析原式=(1-2)+(3-4)+……+(1989-1990)+1991=(-1)×1990÷2+1991=1991-995=996。故正确答案为D。
73、某服装店三月份男装和女装的总销售额为8000元,已知三月份女装销售了50件,每件售价100元,则三月份男装销售额为_____元。
A: 1000B: 2000C: 3000D: 4000
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析由题意可得,三月份男装销售额为8000-50×100=3000元。故正确答案为C。
74、一直角三角形最长边是10厘米,最短边是6厘米,则这个三角形的面积是_____平方厘米。
A: 24B: 30C: 48D: 60
参考答案: A 本题解释:正确答案是A考点几何问题解析解法1:设另一直角边长为b,根据勾股定理有: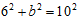 解得b=8,则三角形面积为6×8÷2=24平方厘米,答案为A。解法2:由题干数据可知,该直角三角形三边长符合5:4:3的勾股比例,则另外一条直角边为6×(4/3)=8厘米,故三角形面积为6×8÷2=24平方厘米,答案为A。标签勾股定理
解得b=8,则三角形面积为6×8÷2=24平方厘米,答案为A。解法2:由题干数据可知,该直角三角形三边长符合5:4:3的勾股比例,则另外一条直角边为6×(4/3)=8厘米,故三角形面积为6×8÷2=24平方厘米,答案为A。标签勾股定理
75、某市为鼓励节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按0.45元/吨收费;超过10吨而不超过20吨的部分,按0.80元/吨收费;超过20吨的部分按1.50元/吨收费,某月甲户比乙户多缴水费7.10元,乙户比丙户多缴水费3.75元。问甲、乙、丙该月各缴水费多少元(按整吨收费)?_____
A: 16元,8.9元,5.15元B: 14元,6.9元,3.15元C: 15元,7.9元,4.15元D: 13元,5.9元,2.15元
参考答案: B 本题解释:参考答案:B题目详解:解法一:如果直接设所缴水费为未知数,等量关系不明显,列方程难度太大,所以可间接设他们的用水量为未知数。设丙户用水为 吨(
吨( 为整数,且
为整数,且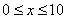 ).乙户用水为
).乙户用水为 吨(
吨( 为整数,且
为整数,且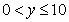 ),因乙户比丙户多缴3.75元,则有
),因乙户比丙户多缴3.75元,则有 ,即
,即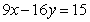 。因为3能整除9和15,但不能整除16,故3必能整除
。因为3能整除9和15,但不能整除16,故3必能整除 ,即
,即 是3的倍数。又经验证,
是3的倍数。又经验证,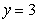 是唯一能使x为整数的值,这时
是唯一能使x为整数的值,这时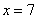 .同理,设甲户用水
.同理,设甲户用水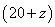 吨(
吨(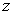 为整数,且
为整数,且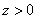 ),因甲户比乙户多缴7.10元,则有:
),因甲户比乙户多缴7.10元,则有: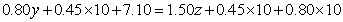 ,即
,即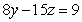 ,把
,把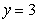 代入,得
代入,得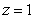 ,故甲户缴纳水费为:
,故甲户缴纳水费为: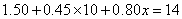 (元),乙户缴纳水费为:
(元),乙户缴纳水费为: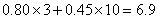 (元),丙户缴纳水费为:
(元),丙户缴纳水费为: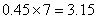 (元)。解法二:观察答案,发现乙的用水量必在10到20吨之间,那么,减去0.45×10=4.5元后,其水费极有可能是0.8的整数倍,只有B符合,验证B中各项,发现正确,故选B考查点:数量关系>数学运算>特殊情境问题>分段计算问题
(元)。解法二:观察答案,发现乙的用水量必在10到20吨之间,那么,减去0.45×10=4.5元后,其水费极有可能是0.8的整数倍,只有B符合,验证B中各项,发现正确,故选B考查点:数量关系>数学运算>特殊情境问题>分段计算问题
76、把一根钢管锯成5段需要8分钟,如果把同样的钢管锯成20段需要多少分钟?_____
A: 32分钟B: 38分钟C: 40分钟D: 152分钟
参考答案: B 本题解释:正确答案是B考点计数模型问题解析重点在切口。钢管锯成5段,则有4个切口,共需要8分钟,因此每个切口花费2分钟。由此把钢管锯成20段,有19个切口,需要用时38分钟,故正确答案为B。
77、一只猫每天吃由食品 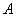 和食品
和食品 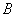 搅拌成的食物
搅拌成的食物 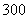 克,食品
克,食品 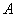 的蛋白质含量为
的蛋白质含量为 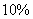 ,食品
,食品 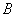 的蛋白质含量为
的蛋白质含量为 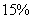 。如果该猫每天需要
。如果该猫每天需要 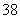 克蛋白质,问食物中食品
克蛋白质,问食物中食品 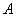 的比重是百分之几?_____
的比重是百分之几?_____
A: 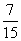 B:
B: 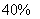 C:
C: 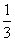 D:
D: 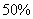
参考答案: A 本题解释:参考答案:A题目详解:应用方程法:设 的比重为
的比重为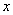 ,可列方程:
,可列方程: ,解得
,解得 ;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合
;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合
78、小明和小强从400米环形跑道的同一点出发,背向而行。当他们第一次相遇时,小明转身往回跑;再次相遇时,小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米,小强每秒跑5米,则在两人第30次相遇时,小明共跑了多少米?
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:【答案】A。
79、四年级一班选班长,每人投票从甲、乙、丙三个候选人中选一人,已知全班共有52人,并且在计票过程中的某一时刻,甲得到17票,乙得到16票,丙得到11票。如果得票最多的候选人将成为班长,甲最少再得多少张票就能够保证当选?_____
A: 1张B: 2张C: 4张D: 8张
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析剩余的票数为:52-17-16-11=8,假设甲是4张,乙得4张,那甲仅以一票的优势当选,此时再少一票甲就不能保证当选,因此甲最少再得4张票就能保证当选,故正确答案为C。
80、一条街上,一个骑车人和一个步行人相向而行,骑车人的速度是步行人的3倍,每个隔10分钟有一辆公交车超过一个行人。每个隔20分钟有一辆公交车超过一个骑车人,如果公交车从始发站每隔相同的时间发一辆车,那么间隔几分钟发一辆公交车? _____
A: 10B: 8C: 6D: 4
参考答案: B 本题解释:B。【解析】设车速V车,人速V人,自行车速3V人,则(V车-V人)×10=20×(V车-3V人),V车=5V人,即车走人4倍位移追上人故T=4×V人×10/5V人=8。
81、某公司计划采购一批电脑,正好赶上促销期,电脑打9折出售,同样的预算可以比平时多买10台电脑。问该公司的预算在平时能多买多少台电脑?_____
A: 60.B: 70C: 80D: 90
参考答案: D 本题解释:【答案】D。解析:设平时可以购买x台,电脑打折前价格为100,则打折后为90,依题意100x=90(x+10),解得=90。
82、(2003广东,第9题)从装满100克浓度为 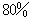 的盐水杯中倒出40克盐水倒人清水将杯倒满,这样反复三次后,杯中盐水的浓度是_____。
的盐水杯中倒出40克盐水倒人清水将杯倒满,这样反复三次后,杯中盐水的浓度是_____。
A:  B:
B:  C:
C:  D:
D: 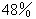
参考答案: A 本题解释:参考答案:A题目详解:根据题意:每次操作后,酒精浓度变为原来的(100-40)/100=0.6;故反复三次后浓度变为:80%×0.6×0.6×0.6=17.28%;所以,选A。考查点:数量关系>数学运算>浓度问题>不同溶液混合
83、某三年制普通初中连续六年的在校生人数分别为:X1,X2,X3,X4,X5,X6.假设该校所有学生都能顺利毕业,那么前三年的入学学生总数与后三年的入学学生总数之差为_____
A: (X1+X2+X3)-(X4+X5+X6) B: X1-X4C: X3-X6 D: (X3-X1)-(X6-X4)
参考答案: C 本题解释:【解析】C.考查整体思维。前三年入学学生人数本质上就是第三年的在校生人数X3(第三年在校生的初三、初二、初一分别为前三年的入学人数),类似的,X6即为后三年的入学人数。故答案为X3-X6.
84、(2006江苏,第7题)已知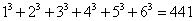 ,则:
,则: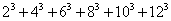 的值是多少?_____
的值是多少?_____
A: 3968B: 3188C: 3528D: 2848
参考答案: C 本题解释:参考答案:C题目详解:观察题干,发现: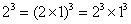 ,
,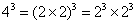 ,
, ,
, ,
,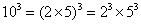 ,
,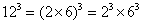 ;那么,
;那么,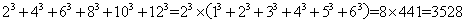 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
85、某S为自然数,被10除余数是9,被9除余数是8,被8除余数是7,已知100<S<1000,请问这样的数有几个?_____
A: 5 B: 4 C: 3 D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1,所以这个数字就是几个N的公倍数-1。10,9,8的公倍数为360n(n为自然数),因为100<S<1000,所以有两个数符合条件。
86、共有20个玩具交给小王手工制作完成。规定,制作的玩具每合格一个得5元,不合格一个扣2元,未完成的不得不扣。最后小王共收到56元,那么他制作的玩具中,不合格的共有_____个。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析:设小王制作合格玩具x个,不合格玩具y个,未完成的有z个。则x+y+z=20,5x-2y=56。为不定方程组,将选项代入验证,仅当y=2时,x与z有正整数解。故正确答案为A。
87、小蔡去超市购物,她买了1.6千克苹果,4磅食油和3.8市斤芦柑。请问小蔡买的这三种食品最重的是哪一种?_____
A: 苹果B: 食油C: 芦柑D: 三者一样重
参考答案: C 本题解释:正确答案是C考点其他解析本题主要考查不同单位之间的数量比较,做此类题目,应首先换算为同一单位。1磅=0.454千克,1市斤=0.5千克,故:4磅=1.816千克,3.8市斤=1.9千克,所以1.6<1.816<1.9,故正确答案为C。
88、水池装有一个排水管和若干个每小时注水量相同的注水管,注水管注水时,排水管同时排水,若用12个注水管注水,8小时可注满水池,若用9个注水管,24小时可注满水,现在用8个注水管注水,那么可用_____注满水池。
A: 12小时B: 36小时C: 48小时D: 72小时
参考答案: D 本题解释:正确答案是D考点牛吃草问题解析设原有水量为N,每小时排水量为Y,可得如下:N=(12-Y)×8=(9-Y)×24,解得N=36,Y=7.5;若用8个注水管,注满时间为t,则有36=(8-7.5)×t,解得t=72小时,故正确答案为D。
89、 _____
_____
A: AB: BC: CD: D
参考答案: A 本题解释:正确答案是A考点趣味数学问题解析设空白图案为a,交叉图案为b,钟表图案为c,故可得如下:a+c×3=a×2+b×2,a+b×2=c×2+a×3,解得c=3a,b=4a;则可得a×2+b=6a=2c,故正确答案为A。
90、41个学生要坐船过河,渡口处只有一只能载4人的小船(无船工),他们要全部渡过河去,至少要使用这只小船渡河多少次_____
A: 23B: 24C: 27D: 26
参考答案: C 本题解释:【答案】C。解析:4个人渡过去,1个人回来,因此每2次渡河可以渡过去3个学生.41=3×13+2,因此一共需要13×2+1=27次。
91、人们将1/10表示为1月10日,也有人将1/10表示为10月1日,这样一年中就有不少混淆不清的日期了,当然,8/15和15/8只能表示为8月15日,那么一年中像这样不会搞错的日期最多会有多少天?_____
A: 221B: 222C: 216D: 144
参考答案: B 本题解释:正确答案是B考点多位数问题解析由题意可分析出,会搞错的日期有这样的特征:(1~12)/(1~12),共有12×12=144,当为闰年366天时,不会搞错的日期最多:366-144=222,故正确答案为B。备注:事实上,本题没有正确选项,因为在144种中,像1/1、2/2、······、12/12这些共12种情况,也是不会搞错的日期,故不会搞错的日期最多:222+12=234,正确答案应该是234。标签构造调整
92、相同表面积的四面体,六面体,正十二面体以及正二十面体,其中体积最大的是_____。
A: 四面体B: 六面体C: 正十二面体D: 正二十面体
参考答案: D 本题解释:正确答案是D考点几何问题解析根据等量最值原理,同样表面积的空间几何图形,越接近于球,体积越大。而四个选项中,正二十面体最接近于球,所以体积最大。故正确答案为D。
93、要从三男两女中安排两人周日值班,至少有一名女职员参加,有多少种不同的安排方法?_____
A: 7B: 10C: 14D: 20
参考答案: A 本题解释:参考答案:A题目详解:从5个人中安排两人值班:有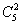 种情况;没有女职员参加:有
种情况;没有女职员参加:有 种情况,至少有一名女职员参加:有
种情况,至少有一名女职员参加:有 种情况;所以,选A。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
种情况;所以,选A。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
94、某矿井发生透水事故,且矿井内每分钟涌出的水量相等,救援人员调来抽水机抽水,如果用两台抽水机抽水,预计40分钟可抽完;如果用4台同样的抽水机,16分钟可抽完。为赢得救援时间,要在10分钟内抽完矿井内的水,那么至少需要抽水机_____。
A: 5台B: 6台C: 7台D: 8台
参考答案: B 本题解释:正确答案是B考点牛吃草问题解析解析1:假定矿井原有水量为N,每分钟涌入的水量为n,根据题意可得N=(2-n)×40,N=(4-n)×16,解得n=2/3,N=160/3,因此要在10分钟内抽完矿井内的水需要抽水机为160/3÷10+2/3=6台。公式:在牛吃草模型背景下,公式为N=(牛数-x)×天数,其中N表示原有草量的存量,以牛数与天数的乘积来衡量;x表示专门吃新增加草量所需要的牛数。解析2:设每台抽水机每分钟抽水1个单位,那么,每分钟进水量为(2×40-4×16)÷(40-16)=2/3个单位,原来的积水量为2×40-(2/3)×40=160/3,那么10分钟内抽完水,需要[(160/3)+10×(2/3)]÷10=6台。故正确答案为B。标签赋值思想
95、一个长方形,它的周长是32米,长是宽的3倍。这个长方形的面积是多少平方米?_____
A: 64B: 56C: 52D: 48
参考答案: D 本题解释:D设宽为x则长为3x,则2(x+3x)=32,则x=4,故面积为48平方米。
96、甲、乙两包糖的质量比是4∶1,如果从甲包取出10克放入乙包后,甲、乙两包糖的质量比变为7∶5,那么两包糖质量的总和是多少克?_____
A: 32B: 46.213C: 48.112D: 50
参考答案: B 本题解释:B[解析]在10克糖未取出前,甲包糖占总质量的45,从甲包取出10克放入乙包后,甲包糖占总质量的712,这就是说比原来减少了45-712=1360,这正好是10克糖对应的份数,这也就是说10克糖占总质量的1360,故总质量是10÷13/60=600/13=46.213(克)故本题应选B。
97、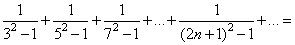 _____
_____
A: 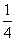 B: 1C:
B: 1C: 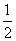 D: 无法计算
D: 无法计算
参考答案: A 本题解释:参考答案:A题目详解:前n项和为: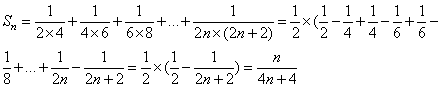 故其极限为
故其极限为 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
98、(2009江苏A类)对正实数定义运算,若 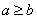 ,则
,则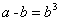 ; 若
; 若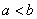 ,则
,则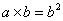 。由此可知,方程
。由此可知,方程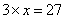 的解是:_____ B: 9C:
的解是:_____ B: 9C: 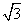 D: 3,
D: 3,
参考答案: D 本题解释:参考答案 题目详解:根据题意可知,若
题目详解:根据题意可知,若 ,则
,则 ,即
,即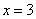 ;若
;若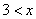 ,则
,则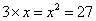 ,即只能有
,即只能有 。因此,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。因此,选D。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
99、海岛上信号站的值班员总用红、黄、白三色各三面旗向附近海域出示旗语,在旗杆上纵排挂,可以是一面、二面、三面。那么这样的旗语有多少种?_____
A: 21B: 27C: 33D: 39
参考答案: D 本题解释:参考答案 题目详解:如果是一面旗:有3种旗语;如果是二面旗:有
题目详解:如果是一面旗:有3种旗语;如果是二面旗:有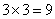 种旗语;如果是三面旗:有
种旗语;如果是三面旗:有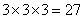 种旗语,因此,一共有
种旗语,因此,一共有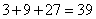 种旗语。所以,选D。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
种旗语。所以,选D。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
100、有甲、乙两项工程,张师傅单独完成甲工程需6天,单独完成乙工程需30天,李师傅单独完成甲工程需18天,单独完成乙工程需24天,若合作两项工程,最少需要的天数为:_____
A: 16天B: 15天C: 12天D: 10天
参考答案: A 本题解释:【答案】A。中解析:分析题意可知,张师傅作甲工程的效率较高,李师傅做乙工程的效率较高,因此李师傅做乙工程,张师傅先用6天完成甲工程,之后与李师傅异同完成乙工程,这样所需的天数最少。