微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、地铁检修车沿地铁线路匀速前进,每6分钟有一列地铁从后面追上,每2分钟有一列地铁迎面开来。假设两个方向的发车间隔和列车速度相同,则发车间隔是_____。
A: 2分钟B: 3分钟C: 4分钟D: 5分钟
参考答案: B 本题解释:【答案】B。解析:此题为水速问题的变种,设两列地铁间的距离为1,则二者速度差为1/6,速度和为1/2,由水速问题的公式得,地铁的速度为(1/6+1/2)÷2=1/3,即3分钟发车一次。
2、甲、乙两地相距100千米,张先骑摩托车从甲出发,1小时后李驾驶汽车从甲出发,两人同时到达乙地。摩托车开始速度是50千米/小时,中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟,那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 1(1/2)C: 1/3D: 2
参考答案: C 本题解释:C解析:汽车行驶100千米需100÷80=1(1/4)(小时),所以摩托车行驶了1(1/4)+1+,1/6=2(5/12)(小时)。如果摩托车一直以40千米/小时的速度行驶,2(5/12)小时可行驶96(2/3)千米,与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷(50-40)=1/3(小时)。故本题选C。
3、甲乙两人参加射击比赛,规定每中一发记5分,脱靶一发倒扣3分,两人各打了10分子弹后,分数之和为52,甲比乙多得了16分,问甲中了多少发?_____
A: 9B: 8C: 7D: 6
参考答案: B 本题解释:【答案】B。解析:甲、乙分数之和为52,差为16,则甲为(52+16)÷2=34分,根据鸡兔同笼公式可得,甲中了(34+3×10)÷(5+3)=8发。
4、现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。若从甲中取2100克,乙中取700克混合而成的消毒浓度为3%;若从甲中取900克,乙中取2700克,则混合而成的溶液的浓度为5%。则甲、乙两种消毒溶液的浓度分别为_____。
A: 3%6%B: 3%4%C: 2%6%D: 4%6%
参考答案: C 本题解释:【答案】C。解析:设两种溶液的浓度分别为a、b,则可列方程2100a+700b=(2100+700)×3%,900a+2700b=(900+2700)×5%,解得a=2%,仅C选项符合,故正确答案为C。老师点睛:甲中去2100克,乙中取700克混合而成的消毒溶液浓度为3%,则甲、乙两溶液的浓度必然是一个比3%大,一个比3%小,只有C选项符合,故正确答案为C。
5、有一笔奖金,按1:2:3的比例来分,已知第三人分450元,那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知,这笔奖金共分为6份,而分到3份的第三人拿到了450元,则6份当是450×2=900元。所以正确答案为C项。
6、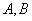 两地相距105千米,甲、乙两人骑自行车分别从两地同时相向而行,甲从
两地相距105千米,甲、乙两人骑自行车分别从两地同时相向而行,甲从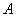 地出发,出发后经
地出发,出发后经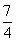 小时相遇,接着两人继续前进,在他们相遇3分钟后,一直以每小时40千米速度行驶的甲在途中与迎面而来的丙相遇,丙在与甲相遇后继续前进,在
小时相遇,接着两人继续前进,在他们相遇3分钟后,一直以每小时40千米速度行驶的甲在途中与迎面而来的丙相遇,丙在与甲相遇后继续前进,在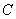 地赶上乙。如果开始时甲的速度比原速每小时慢20千米,而乙的速度比原速每小时快2千米。那么甲、乙就会在C地相遇,丙的骑车速度为_____千米/小时。
地赶上乙。如果开始时甲的速度比原速每小时慢20千米,而乙的速度比原速每小时快2千米。那么甲、乙就会在C地相遇,丙的骑车速度为_____千米/小时。
A: 20B: 24C: 23D: 23.2
参考答案: D 本题解释:参考答案 题目详解:两人的速度和是:
题目详解:两人的速度和是: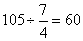 千米/小时,乙的速度是:60-40=20千米/小时。甲速度降低20千米/小时,乙速度提高2千米/小时后,两人的速度和:20+22=42千米/小时,相遇用时为
千米/小时,乙的速度是:60-40=20千米/小时。甲速度降低20千米/小时,乙速度提高2千米/小时后,两人的速度和:20+22=42千米/小时,相遇用时为 小时;甲行了
小时;甲行了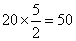 千米,因此
千米,因此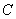 距离
距离 点50千米,第一次甲行了1小时48分钟后与丙相遇,此时距离
点50千米,第一次甲行了1小时48分钟后与丙相遇,此时距离 点72千米,第一次相遇乙走了36千米,距离
点72千米,第一次相遇乙走了36千米,距离 点69千米,丙与乙的追及距离是
点69千米,丙与乙的追及距离是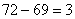 千米;最终丙在
千米;最终丙在 点追上乙,乙走了
点追上乙,乙走了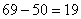 千米用时为
千米用时为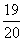 小时,则丙的速度是:
小时,则丙的速度是: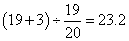 千米/小时。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
千米/小时。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
7、有一食品店某天购进了6箱食品,分别装着饼干和面包,重量分别为8、9、16、20、22、27千克。该店当天只卖出1箱面包,在剩下的5箱中饼干的重量是面包的两倍,则当天食品店购进了_____千克面包。
A: 44B: 45C: 50D: 52
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由剩下的饼干重量是面包的两倍可知,剩下5箱的总重量一定能被3整除;6箱的总重量是8+9+16+20+22+27=102千克,也能被3整除,因此卖掉的一箱面包的重量也能被3整除,只能是9千克或27千克。若卖掉的一箱面包的重量是9千克,则剩下的面包重(102-9)÷3=31千克,剩余的各箱重量无法组合得到31。所以卖出的面包重27千克,剩余面包重(102-27)÷3=25千克。因此共购进了27+25=52千克面包,故正确答案为D。
8、下列数中最大的是_____。
A: 599×601B: 598×602C: 590×610D: 500×700
参考答案: A 本题解释:正确答案是A考点计算问题解析对比可见,四组乘数中,其前一个乘数依次减小,后一个乘数依次增大。只要对比A,D两项的数字孰大孰小就可以知道答案了。599×601≈36000,500×700=35000。A项的数明显大于D项,由此可知A项的数最大。故正确答案为A。
9、如果甲比乙多20%,乙比丙多20%,则甲比丙多百分之多少?_____
A: 44B: 40C: 36D: 20
参考答案: C 本题解释:答案:C【解析】这道题实际只要考虑五个五个一数最后剩一个,三个三个一数最后剩一个,即可。这两个最好思考。只有501与421一幕了然,除以5余1。而501能被3整除,只有42。
10、甲单位义务植树一公里,乙单位紧靠甲单位又植树一公里,如果按10米植一棵树的话,两单位共植树多少棵?_____
A: 199B: 200C: 201D: 202
参考答案: C 本题解释:参考答案:C题目详解:此题要求两单位的植树总数,则分甲单位植树的棵数和乙单位植树的棵数。甲单位在一公里内植树,则两端均可植一棵树,带入两端均植树问题的公式:棵数=总长÷间距+1=1000÷10+1=101棵树;乙单位紧靠着甲单位植树,则有一端不需要植树,带入只有一端植树问题的公式:棵数=总长÷间距=1000÷10=100棵树。因此,甲、乙共植树:101+100=201棵。所以,选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树
11、一汽船往返于两码头间,逆流需要10小时,顺流需要6小时。已知船在静水中的速度为12公里/小时。问水流的速度是多少公里/小时?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:参考答案:.B题目详解:根据题意,设水流的速度是x公里/小时,两码头间距离为y公里。确定顺流航行速度:(x+12)公里/小时,确定逆流航行速度:(12-x)公里/小时。则有: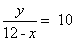 ,
,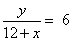 ,解得
,解得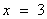 ;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
;所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
12、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇?_____
A: 8点48分 B: 8点30分 C: 9点 D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
13、 _____
_____
A: AB: BC: CD: D
参考答案: D 本题解释:正确答案是D考点几何问题解析 故正确答案为D。
故正确答案为D。
14、从3双完全相同的鞋中,随机抽取一双鞋的概率是_____。
A: 1/2B: 3/5C: 1/6D: 1/3
参考答案: B 本题解释:正确答案是B考点概率问题解析
15、如图:甲,乙二人分别从A,B两地同时相向出发,往返于A、B之间,第一次相遇在距A地30公里处,第二次相遇地点在距第一次相遇地右边10公里处:问A、B两点相距多远?_____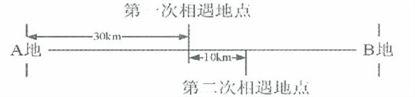
A: 90B: 75C: 65D: 50
参考答案: C 本题解释:参考答案:C题目详解:解法一:两人第一次相遇,共同走完了一个全程,第二次相遇共同走完了3个全程。第一次相遇甲走了30千米,那么第2次相遇时,甲共走了3×30=90千米,实际上甲还差30+10=40千米才走完两个全程。AB两地的距离是:(90+40)÷2=65公里。解法二:“单岸型”,两次相遇问题: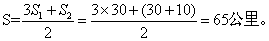 所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
16、(2006北京社招,第11题)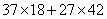 的值是_____。
的值是_____。
A: 1800B: 1850C: 1900D: 2000
参考答案: A 本题解释:参考答案:A题目详解:应用因式分解法: ;
; 考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
17、甲乙两个工厂的平均技术人员比例为45%,其中甲厂的人数比乙厂多12.5%,技术人员的人数比乙厂的多25%,非技术人员人数比乙厂多6人。甲乙两厂共有多少人?_____
A: 680B: 840C: 960D: 1020
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析由题干中"甲厂人数比乙厂多12.5%"可知甲、乙两厂总人数之比为9:8,则可假设甲厂总人数有9n,乙厂总人数有8n,甲乙总人数为17n,故总人数一定能被17整除,排除选项B、C;在A和D之间选择,直接代入A选项,则有680=17n,n=40,则甲厂共360人,乙厂共320人,两厂的技术人员总数为680×45%=306人,甲厂技术人员有170人,非技术人员为190人,乙厂有技术人员136人,非技术人员184人,甲乙两厂的非技术人员相差190-184=6人,满足题意,验证成立。故正确答案为A。标签直接代入数字特性
18、已知ab+6=c,其中a和b都是小于1000的质数,c是偶数,那么c的最大的数值是多少?_____
A: 1500B: 1600C: 2000D: 2100
参考答案: C 本题解释:参考答案:C题目详解:因为和c是偶数,加数中6是偶数:所以ab的积也是一个偶数;因为两个都是质数:所以当中必有一个是2;要想使得和c最大:那么另一个质数就必须是小于1000的最大的质数997;所以c=2×997+6=2000;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
19、小伟参加英语考试,共50道题,满分为100分,得60分算及格。试卷评分标准为做对一道加2分。做错一道倒扣2分,结果小伟做完了全部试题但没及格。他发现,如果他少做错两道题就刚好及格了。问小伟做对了几道题?_____
A: 32 B: 34 C: 36 D: 38
参考答案: D 本题解释:【答案】D。解析:少做错2道刚好及格,多做对一道多得4分,所以小伟实际得了60-2×4=52分。设作对x道,则2x-2(50-x)=52,解得x=38。
20、桌面上有两个半径分别为2厘米和40厘米的圆环,让小圆环沿着大圆环外边缘滚动一圈,则小圆环滚动的圈数是:_____
A: 9B: 25C: 49D: 81
参考答案: B 本题解释:【答案解析】如果两人不调头走,两人相遇需要1350÷1000÷(4+5)×60=9分钟。如果以初始方向为正方向,则两个人分别走了1、-3、5、-7、……分钟的路程,由于9=1-3+5-7+9-11+13-15+17,则出发后1+3+5+7+9+11+13+15+17=81分钟两人相遇。
21、某品牌的电冰箱,甲商场比乙商场的进价多10%,如果甲商场按30%的利润定价,乙商场按40%的利润定价,则甲商场的定价比乙商场多45元,那么乙商场的进价是多少元?_____
A: 2100B: 1800C: 1500D: 2600
参考答案: C 本题解释:正确答案是C考点经济利润问题解析假设乙商场进价x元,则甲商场进价为1.1x元,根据题意得,1.3×1.1x-1.4x=45,解得x=1500,故正确答案为C。
22、某学校的全体学生刚好排成一个方阵,最外层的人数是108人,则这个学校共有多少学生?_____
A: 724人B: 744人C: 764人D: 784人
参考答案: D 本题解释:正确答案是D考点计数模型问题解析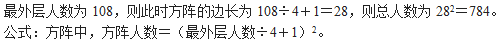 故正确答案为D。秒杀技要拼成方阵,则人数必然为完全平方数,仅D符合。故正确答案为D。
故正确答案为D。秒杀技要拼成方阵,则人数必然为完全平方数,仅D符合。故正确答案为D。
23、7个同学排成两排照相,前排3人,后排4人,共有_____种站法。
A: 1680B: 2400C: 2520D: 5040
参考答案: D 本题解释:【解析】相当于把7个元素放在预先指定好的7个不同位置上,因此,是7个同学的全排列,共有P77=5040种站法。
24、一个长方形,若将短边长度增加4厘米,长边长度增加一倍,则面积是原来的3倍,若将长边缩短8厘米,就成正方形,则原长方形面积是多少平方厘米?_____
A: 180B: 128C: 84D: 48
参考答案: B 本题解释:正确答案是B考点几何问题解析根据题干设短边为n,则长边为n+8。则有2(n+4)(n+8)=3n(n+8),可得n=8,故原长方形面积=8×16=128。所以正确答案为B。
25、某单位派60名运动员参加运动会开幕式,他们着装白色或黑色上衣,黑色或蓝色裤子。其中有12人穿白上衣蓝裤子,有34人穿黑裤子,29人穿黑上衣,那么穿黑上衣黑裤子的有多少人?_____
A: 12B: 14C: 15D: 29
参考答案: C 本题解释:正确答案是C 考点容斥原理问题解析由“有34人穿黑裤子”可知穿蓝裤子的人数为60-34=26,又知“有12人穿白上衣蓝裤子”,则穿黑上衣蓝裤子的人数为26-12=14,而又有“29人穿黑上衣”,因此穿黑上衣黑裤子的人数为29-14=15,故正确答案为C。
26、袋中有7只白球,3只红球,白球中有4只木球,3只塑料球;红球中有2只木球,1只塑料球。现从袋中任取1球,并且每只球被取到的可能性相同。若已知取到的球是白球,问它是木球的概率是多少?_____
A: 4/7B: 7/25C: 2/25D: 2/5
参考答案: A 本题解释:参考答案:A题目详解:取到白球中的木球的概率: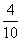 ;取到白球的概率为:
;取到白球的概率为: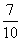 ;根据条件概率公式:
;根据条件概率公式: ;所以,选A。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选A。考查点:数量关系>数学运算>概率问题>条件概率
27、某部队战士排成了一个6行、8列的长方阵。现在要求各行从左至右1,2,1,2,1,2,1,2报数,再各列从前到后1,2,3,1,2,3报数。问在两次报数中,所报数字不同的战士有_____。
A: 18个B: 24个C: 32个D: 36个
参考答案: C 本题解释:正确答案是C考点计数模型问题解析 标签画图分析
标签画图分析
28、幼儿园里,老师将一堆桃子分给同学,如果每个同学分3个则余2个,如果每个同学分4个,则有两个同学分不到,该班有多少个同学?_____
A: 10B: 12C: 15D: 18
参考答案: A 本题解释:A【解析】设共有x个同学,由题意得3x+2=4(x-2),解得x=10。
29、甲、乙、丙、丁四人做纸花,已知甲、乙、丙三人平均每人做了37朵,乙、丙、丁三人平均每人做了39朵,已知丁做了41朵,问甲做了多少朵?_____
A: 35朵B: 36朵C: 37朵D: 38朵
参考答案: A 本题解释:正确答案是A考点平均数问题解析由“甲、乙、丙三人平均每人做了37朵”和“丁做了41朵”可知四人一共做了:37×3+41=152,又知“乙、丙、丁三人平均每人做了39朵”,所以甲做了:152-39×3=35朵,故正确答案为A。
30、一个俱乐部,会下象棋的有69人,会下围棋的有58人,两种棋都不会下的有12人,两种棋都会下的有30人,问这个俱乐部一共有多少人?_____
A: 109人B: 115人C: 127人D: 139人
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析由两集合容斥原理公式得俱乐部共有(69+58-30)+12=109人,故正确答案为A。两集合容斥原理公式:|A∪B|=|A|+|B|﹣|A∩B|。标签两集合容斥原理公式公式应用
31、用1,2,3,4,5这五个数字组成没有重复数字的自然数,从小到大顺序排列:1,2,3,4,5,12,……,54321。其中,第206个数是_____
A: 313 B: 12345 C: 325 D: 371
参考答案: B 本题解释:B。由1、2、3、4、5组成的没有重复数字的一位数共有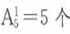 ;二位数共有个
;二位数共有个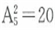 ;三位数共有个
;三位数共有个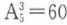 ;四位数共有个
;四位数共有个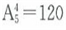 ;至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个;那么第206个数是第一个由1、2、3、4、5组成的五位数,即最小的五位数12345。
;至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个;那么第206个数是第一个由1、2、3、4、5组成的五位数,即最小的五位数12345。
32、某校办公司生产一批新产品,现有两种销售方案:方案一,在这学期开学时售出该产品,可获利30000元,然后将该批产品的成本和已获利的30000元再进行投资,到这学期结束时可获利 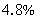 ;方案二,在这学期结束时售出该产品,可获得利润35940元,但要付成本的
;方案二,在这学期结束时售出该产品,可获得利润35940元,但要付成本的 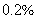 作保管费,则成本超过多少元时采用方案一比较好?_____
作保管费,则成本超过多少元时采用方案一比较好?_____
A: 90000B: 93750C: 690000D: 718750
参考答案: A 本题解释:参考答案:A题目详解:设成本超过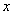 时,采用方案一比较好。则方案一利润为:(x+30000)×4.8%+30000;方案二利润为:35940-0.2%×x;要采用方案一,则要方案一利润>方案二利润,即
时,采用方案一比较好。则方案一利润为:(x+30000)×4.8%+30000;方案二利润为:35940-0.2%×x;要采用方案一,则要方案一利润>方案二利润,即 解得,x>90000。所以,选A。考查点:数量关系>数学运算>利润利率问题>其他利润相关问题
解得,x>90000。所以,选A。考查点:数量关系>数学运算>利润利率问题>其他利润相关问题
33、有编号为1-13的卡片,每个编号有4张,共52张卡片。问至少摸出多少张,就可保证一定有3张卡片编号相连?_____
A: 27张B: 29张C: 33张D: 37张
参考答案: D 本题解释:正确答案是D考点抽屉原理问题解析抽屉原理,考虑最差的情况,抽出的卡片都是两张卡片编号相连,即编号为1、2、4、5、7、8、10、11、13的卡片各抽出4张,共36张,此时抽出任意一张就能保证一定有3张卡片编号相连,故最少抽出36+1=37张,故正确答案为D。标签构造调整
34、小强前三次的数学测验平均分是88分,要想平均分达到90分以上,他第四次测验至少要得多少分?_____
A: 98分B: 92分C: 93分D: 96分
参考答案: D 本题解释:【答案】D。解析:如果第四次测验后平均分数达到90分,则总分为90×4=360(分),第四次测验至少要360-88×3=96(分)。故正确答案为D。
35、(2008广东,第13题)60个人上身着白上衣或黑上衣,下身着蓝裤子或黑裤子。其中有12个人穿白上衣蓝裤子,有34个人穿黑裤子,有29个人穿黑上衣,求身着黑裤子黑上衣多少人?_____
A: 13B: 14C: 15D: 20
参考答案: C 本题解释:参考答案:C题目详解:解法一:根据题意,设穿黑裤子黑上衣的人数有x人。根据公式“黑裤子数+黑上衣数-黑裤子黑上衣数=总数-白衣服蓝裤子数”可得: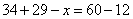 ,解得
,解得 。所以,选C。解法二:根据题意,设上衣分别为1、2,裤子分别为3、4。总共4种穿衣的情况:
。所以,选C。解法二:根据题意,设上衣分别为1、2,裤子分别为3、4。总共4种穿衣的情况: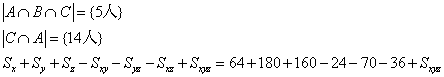 ;
;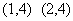 ;又因为:
;又因为: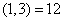 ,
,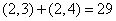 ,
,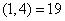 ,
, ;所以,可得:
;所以,可得: 所以,选C。解法三:根据题意,可知:60名运动员中有34人穿黑裤子,则剩下的60-34=26人穿蓝色裤子。而穿蓝色裤子的26人中有12人穿白上衣,那么剩下的26-12=14人穿黑上衣且蓝裤子又穿黑上衣的29人中有14人穿蓝裤子,那么剩下的人穿黑裤子且黑上衣,有29-14=15人。如图所示:
所以,选C。解法三:根据题意,可知:60名运动员中有34人穿黑裤子,则剩下的60-34=26人穿蓝色裤子。而穿蓝色裤子的26人中有12人穿白上衣,那么剩下的26-12=14人穿黑上衣且蓝裤子又穿黑上衣的29人中有14人穿蓝裤子,那么剩下的人穿黑裤子且黑上衣,有29-14=15人。如图所示: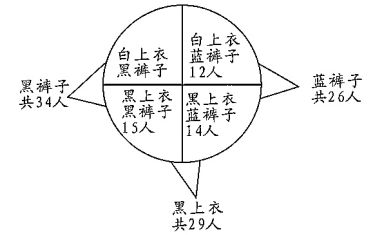 所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
36、1/3,4/13,14/39,12/41以上这四个数中,最大的数为最小的数的几倍?_____
A: 7/6倍B: 14/13倍C: 41/36倍D: 287/234倍
参考答案: D 本题解释:正确答案是D考点计算问题解析 标签尾数法
标签尾数法
37、一个两位数除以一个一位数,商仍是两位数,余数是8。问:被除数、除数、商以及余数之和是多少?_____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析:猜证结合的98÷10=9余8,10+98+9+8=125。
38、某技校安排本届所有毕业生分别去甲、乙、丙3个不同的工厂实习。去甲厂实习的毕业生占毕业生总数的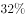 ,去乙厂实习的毕业生比甲厂少6人,且占毕业生总数的
,去乙厂实习的毕业生比甲厂少6人,且占毕业生总数的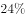 。问去丙厂实习的人数比去甲厂实习的人数:_____
。问去丙厂实习的人数比去甲厂实习的人数:_____
A: 少9人B: 多9人C: 少6人D: 多6人
参考答案: B 本题解释:正确答案是B,解析:根据题意去甲厂实习的人数占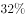 ,去乙厂实习的人数占
,去乙厂实习的人数占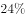 ,因此去丙厂实习的人数占
,因此去丙厂实习的人数占 ,故去丙厂的人数比去甲厂多
,故去丙厂的人数比去甲厂多 ;而去甲厂实习的人数比去乙厂的多
;而去甲厂实习的人数比去乙厂的多 ,为6人,故去丙厂的人数比去甲厂的应多
,为6人,故去丙厂的人数比去甲厂的应多 。故正确答案为B。考点:计算问题
。故正确答案为B。考点:计算问题
39、在一个口袋中有lO个黑球、6个白球、4个红球.至少从中取出多少个球才能保证其中有白球? _____
A: 14B: 15C: 17D: 18
参考答案: B
40、学校文艺组每人至少会演奏一种乐器,已知会拉手提琴的有24人,会弹电子琴的有17人,其中两样都会的有8人。这个文艺组一共有多少人?_____
A: 25B: 32C: 33D: 41
参考答案: C 本题解释:参考答案:C题目详解:根据题意,设:A={{会拉手风琴的}},B={{会弹电子琴的}},因此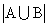 ={{文艺组的人}},
={{文艺组的人}},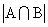 ={{两样都会的}},由两个集合的容斥原理可得:
={{两样都会的}},由两个集合的容斥原理可得: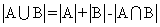 =
=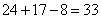 。所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
。所以,选C。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
41、南方某城市的一家企业有90%的员工是股民,80%的员工是“万元户”,60%的员工是打工仔,那么,这家企业的“万元户”中至少有多大比例是股民?_____
A: 67.5%B: 75%C: 87.5%D: 91.5%
参考答案: C 本题解释:C【解析】先假设这个企业共有员工100人,其中:90人是股民,即可知10人不是股民;80人是“万元户”,即可20人不是“万元户”;60人是打工仔。因此,“万元户”的80人至少有80-10=70人是股民,他们占全体“万元户”的70÷80×100%=87.5%。可见,本题正确答案为C。
42、甲、乙两个港口相距120公里,船从甲到乙顺水航行需要5小时,从乙到甲逆水航行需要20小时。现有A、B两条船分别从甲、乙两港同时出发,相向而行,5小时后C船从甲港出发驶往乙港,则A、B相遇后_____小时,B、C相遇。
A: 6.5B: 5.2C: 4D: 3
参考答案: C 本题解释:参考答案:.C题目详解:船顺水航行速度为: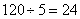 (公里/小时),船逆水航行速度为:
(公里/小时),船逆水航行速度为: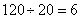 (公里/小时)。设
(公里/小时)。设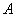 、
、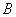 两船航行
两船航行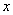 小时后相遇,根据题意可得:
小时后相遇,根据题意可得: ,解得
,解得 ;设
;设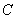 船开出
船开出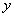 小时后与
小时后与 船相遇,过程如图所示:
船相遇,过程如图所示: 由此可知:
由此可知: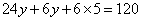 ,解得
,解得 ;
;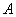 、
、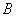 相遇需4小时,相遇后B继续航行1小时后,
相遇需4小时,相遇后B继续航行1小时后,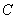 才出发,
才出发,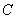 出发3小时后
出发3小时后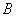 、
、 相遇,从
相遇,从 、B相遇到
、B相遇到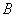 、
、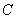 相遇,相隔了
相遇,相隔了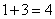 。所以,选C。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
。所以,选C。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
43、一个正方形的一边减少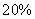 ,另一边增加2,得到长方形的面积与原正方形的面积相等,问正方形面积是多少?_____
,另一边增加2,得到长方形的面积与原正方形的面积相等,问正方形面积是多少?_____
A: 8B: 10C: 16D: 64
参考答案: D 本题解释:参考答案 题目详解:设原来正方形的边长为
题目详解:设原来正方形的边长为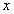 米:
米: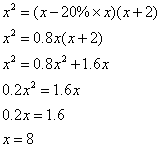 所以原来正方形的边长为8米;所以原来正方形的面积:
所以原来正方形的边长为8米;所以原来正方形的面积: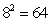 ;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
;所以,选D。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
44、甲、乙两位学生原计划每天自学的时间相同,若甲每天增加自学时间半小时,乙每天减少自学时间半小时,则乙自学6天的时间仅相当于甲自学一天的时间。问:甲、乙原计划每天自学多少分钟?_____
A: 42B: 48C: 56D: 64
参考答案: A 本题解释:参考答案:A题目详解:解法一:原来二者时间相同,现在甲每天增加自学时间半小时,乙每天减少自学时间半小时,甲比乙多自学一个小时,乙自学6天的时间仅相等于甲自学一天的时间,甲是乙的6倍,差倍问题。乙每天减少半小时后的自学时间为: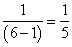 小时=12分钟,乙原计划每天自学时间为:30+12=42分钟,甲原计划每天自学时间为:12×6-30=42分钟。解法二:原来时间相同,现甲多半小时,乙少半小时,现在的两数差是(30+30)=60分钟,现在的差数差是(6-1)=5倍,这样可求出现乙每天自学的时间,加上30分钟,可得原计划每天自学时间。即:(30+30)÷(6-1)+30=12+30=42(分钟)。所以,选A。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
小时=12分钟,乙原计划每天自学时间为:30+12=42分钟,甲原计划每天自学时间为:12×6-30=42分钟。解法二:原来时间相同,现甲多半小时,乙少半小时,现在的两数差是(30+30)=60分钟,现在的差数差是(6-1)=5倍,这样可求出现乙每天自学的时间,加上30分钟,可得原计划每天自学时间。即:(30+30)÷(6-1)+30=12+30=42(分钟)。所以,选A。考查点:数量关系>数学运算>和差倍比问题>和差倍问题
45、 _____
_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:正确答案是C考点计算问题解析
46、有甲、乙两项工程,张师傅单独完成甲工程需6天,单独完成乙工程需30天,李师傅单独完成甲工程需18天,单独完成乙工程需24天,若合作两项工程,最少需要的天数为:_____
A: 16天B: 15天C: 12天D: 10天
参考答案: A 本题解释:【答案】A。中解析:分析题意可知,张师傅作甲工程的效率较高,李师傅做乙工程的效率较高,因此李师傅做乙工程,张师傅先用6天完成甲工程,之后与李师傅异同完成乙工程,这样所需的天数最少。
47、254个志愿者来自不同的单位,任意两个单位的志愿者人数之和不少于20人,且任意两个单位志愿者的人数不同,问这些志愿者所属的单位数最多有几个?_____ B: 1C: 2D: 3
参考答案: B 本题解释:正确答案是C考点趣味数学问题解析设A<B<C<D<E,则必有A+B=17,A+C=25,C+E=42,D+E=45。两两相加,应该有10个数值,因此必有两个重复值。这10个数值相加,必为4的倍数,将题中8个数值相加得261,除以4余1,因此另外两个加和必然除以4余3,重复的两个数在28、31、34、39中,因此这两个数为28、39或28、31,28必为重复值,可知B+C=A+D=28,所以,A=7,B=10,C=18,D=21,E=24,能被6整除的有18、24两个。故正确答案为C。<p>
48、三种动物赛跑,已知狐狸的速度是兔子的2/3,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑_____米。
A: 28B: 14C: 19D: 7
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析根据题意,设兔子、狐狸、松鼠的速度比为6:4:3,一分钟松鼠比狐狸少跑14米,说明一份为14米/分钟,所以兔子和狐狸的速度分别为6×14和4×14,因此半分钟兔子比狐狸多跑(6×14-4×14)÷2=14米,故正确答案为B。秒杀技题目中时间为半分钟,实际上是一个时间陷阱,根据猜题技巧,选项中应有一个干扰选项是正确选项的2倍,只有A、B符合,即B项正确。标签猜题技巧
49、甲、乙、丙三人,甲的年龄比乙的年龄的2倍还大3岁,乙的年龄比丙的年龄的2倍小2岁,三个人的年龄之和是109岁,分别求出甲、乙、丙的年龄_____
A: 63,30,16B: 60,33,16C: 55,38,16D: 40.30.39
参考答案: A 本题解释:参考答案:A题目详解:根据题意,设丙的年龄为 ,则乙的年龄为
,则乙的年龄为 ,甲的年龄为
,甲的年龄为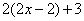 ,可列方程:
,可列方程: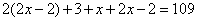 ,解得,
,解得,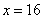 。则乙有30岁,甲有63岁。所以,选A。考查点:数量关系>数学运算>特殊情境问题>年龄问题
。则乙有30岁,甲有63岁。所以,选A。考查点:数量关系>数学运算>特殊情境问题>年龄问题
50、河道赛道长120米,水流速度为2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48 B: 50 C: 52 D: 54
参考答案: C 本题解释: C。
51、甲、乙两人分别从A、B两地同时出发,相向而行,乙的速度是甲的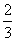 ,相遇后继续前进,甲到达B地,乙到达A地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是3000米,求A、B两地的距离。_____
,相遇后继续前进,甲到达B地,乙到达A地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是3000米,求A、B两地的距离。_____
A: 4500米B: 6500米C: 7500米D: 8650米
参考答案: C 本题解释:参考答案:C题目详解:解法一:设甲的速度为x,则乙的速度为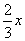 ,第一次相遇的时间为t,从第一次相遇到第二次相遇的时间为y,两地距离为s。由题意可得:
,第一次相遇的时间为t,从第一次相遇到第二次相遇的时间为y,两地距离为s。由题意可得: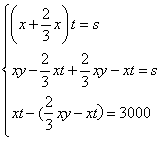 由以上公式解得:s=7500解法二:甲乙速度比是:1:
由以上公式解得:s=7500解法二:甲乙速度比是:1: =3:2第一次相遇的时候:甲行全程
=3:2第一次相遇的时候:甲行全程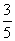 ,乙行全程的
,乙行全程的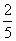 ;第二次相遇是三个全程,甲行了:
;第二次相遇是三个全程,甲行了: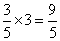 ;那么此时甲距离A地:
;那么此时甲距离A地: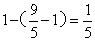 ;那么全程AB:
;那么全程AB: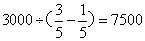 米。解法三:两个人第二次相遇时共走了3个的全程,将全程设为5份。第一次相遇时候乙走了2份,于是知道第二次相遇地点距离第一次相遇地点最短的路程是
米。解法三:两个人第二次相遇时共走了3个的全程,将全程设为5份。第一次相遇时候乙走了2份,于是知道第二次相遇地点距离第一次相遇地点最短的路程是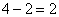 份。依题意这2份路程的长度是3000米,那么A、B两地相距
份。依题意这2份路程的长度是3000米,那么A、B两地相距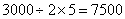 米。所以,选C考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
米。所以,选C考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
52、甲、乙、丙三个班向希望工程捐赠图书,已知甲班有1人捐6册,有2人各捐7册,其余各捐11册,乙班有1人捐6册,有3人各捐8册,其余各捐10册,丙班有2人捐4册,6人各捐7册,其余人各捐9册。已知甲班捐书总数比乙班多28册,乙班比丙班多101册,各班捐书总数在400~550册之间。那么,甲、乙、丙三个班各有多少人?_____
A: 48、50、53B: 49、51、53C: 51、53、49D: 49、53、51
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析甲班比丙班多28+101=129册,则甲班总数在529—550之间;甲班为6+2×7+11n=20+11n,多捐2册就能被11整除,所以甲班总数只能是548(550-2)或537,因此丙班是419或408;丙班为2×4+6×7+9m=50+9m,多捐4册就能被9整除。因此丙班捐了419本,则丙班有(419-50)÷9+8=49人,故正确答案为C。
53、两年前甲的年龄是乙的两倍,五年前乙的年龄是丙的三分之一,丙今年11岁,问今年甲多少岁?_____
A: 12B: 10C: 7D: 5
参考答案: A 本题解释:参考答案:A题目详解:解法一:设今年甲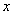 岁,乙
岁,乙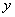 岁,则
岁,则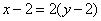 ,
, ,解得,
,解得,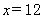 。所以,选A。解法二:五年前乙的年龄是丙的三分之一,丙今年11岁,5年前丙是:
。所以,选A。解法二:五年前乙的年龄是丙的三分之一,丙今年11岁,5年前丙是: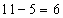 岁,五年前乙是:
岁,五年前乙是: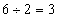 岁,则乙今年为:
岁,则乙今年为: 岁;两年前甲的年龄是乙的两倍,今年乙是7岁,则两年前乙为:
岁;两年前甲的年龄是乙的两倍,今年乙是7岁,则两年前乙为: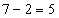 岁,两年前甲为:
岁,两年前甲为: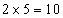 岁,则甲今年为:
岁,则甲今年为: 岁。所以,选A。考查点:数量关系>数学运算>特殊情境问题>年龄问题
岁。所以,选A。考查点:数量关系>数学运算>特殊情境问题>年龄问题
54、某公司甲、乙两个营业部共有50人,其中32人为男性。已知甲营业部的男女比例为5:3,乙营业部的男女比例为2:1,问甲营业部有多少名女职员?_____
A: 18B: 16C: 12D: 9
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设甲营业部有3X名女职员,乙营业部有Y名女职员,则有5X+2Y=32;32+3X+Y=50,解得X=4,Y=6,故甲营业部有3×4=12名女职员,故正确答案为C。秒杀技有题意可知,两个营业部共有50-32=18名女职员,排除A。根据“乙营业部的男女比例为2:1”可知,乙营业部的男职员为偶数,由于男职员的总人数为偶数,则甲营业部的男职员人数同样为偶数。根据“已知甲营业部的男女比例为5:3”,甲营业部的女职员人数能同时被2和3整除,排除B、D,故正确答案为C。
55、某公司三名销售人员2011年的销售业绩如下:甲的销售额是乙和丙销售额的1.5倍,甲和乙的销售是丙的销售额的5倍,已知乙的销售额是56万元,问甲的销售额是_____。
A: 140万元B: 144万元C: 98万元D: 112万元
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由题意,甲=1.5(乙+丙),甲+乙=5丙,将乙=56代入,可得甲=144,丙=40。故答案为B。秒杀技秒杀一:由甲的销售额是乙丙之和的1.5倍,而1.5中含有因子3,因此甲的销售额能被3整除,仅B符合。秒杀二:甲和乙的销售额之和是丙销售额的5倍,因此甲乙销售额之和能够被5整除,其尾数为0或5,在四个选项中仅B符合这一要求。
56、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,而汽车的速度是他速度的5倍,则此人追上小偷需要_____
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:【解析】D。设小偷速度为V,则他的速度2V,汽车的速度10V。l0秒内小偷走了10V,但车子走了100V,所以距离是110V,而他和小偷的速度差为V,即追上小偷需要110秒。
57、真分数a/7化为小数后,如果从小数点后第一位数字开始连续若干数字之和是1992,那么A的值是_____。
A: 6B: 5C: 7D: 8
参考答案: A 本题解释:【答案解析】:由于除7不能整除的的数结果会是‘142857’的循环(这个可以自己测算一下),1+4+2+8+5+7=27,1992/27余数为21,重循环里边可知8+5+7+1=21,所以8571会多算一遍(多重复的一遍,一定在靠近小数点的位置上),则小数点后第一位为8,因此a为6。
58、2010年某种货物的进口价格是15元/公斤,2011年该货物的进口量增加了一半,进口金额增加了20%。问2011年该货物的进口价格是多少元/公斤?_____
A: 10B: 12C: 18D: 24
参考答案: B 本题解释:正确答案是B考点经济利润问题解析假设2010年进口了2公斤,2010年进口金额是30元,2011年进口了3公斤,进口金额是30×(1﹢20%)=36,因此2011年进口价格是36÷3=12元/公斤,故正确答案为B。标签赋值思想
59、甲乙两人计划从A地步行去B地,乙早上7:00出发,匀速步行前往,甲因事耽搁,9:00才出发。为了追上乙,甲决定跑步前进,跑步的速度是乙步行速度的2.5倍,但每跑半小时都需要休息半小时,那么甲什么时候才能追上乙?_____
A: 10:20B: 12:10C: 14:30D: 16:10
参考答案: C 本题解释:正确答案是C考点行程问题解析解析1:设乙步行速度为1,则甲跑步速度为2.5,则9:00时甲乙两人之间的距离为2,5小时后,两人相距2-(2.5×0.5-1)×5=0.75,此时,再经过半小时甲刚好追上乙,即共用了5个半小时,在14:30追上,故正确答案为C。解析2: 标签直接代入
标签直接代入
60、袋子里装有红、蓝两色的小球各12个,先从袋子中拿出一个球,然后将它放回袋子中,混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有_____。
A: 20%B: 25%C: 50%D: 60%
参考答案: C 本题解释:【解析】因为两种颜色的小球数量相等,那么每次抽中其中一种颜色小球的概率均为50%。第一种情况:第一次抽中了红色小球,第二次抽中了蓝色小球,概率是50%×50%一25%;第二种情况:第一次抽中了蓝色小球,第二次抽中了红色小球,概率是50%×50%=25%。那么两次抽中不同颜色的小球的整体概率等于两种情况下的概率之和,即25%+25%=50%,答案为C。
61、某企业组织80名员工一起去划船,每条船乘客定员12人,则该企业最少要租船_____条。
A: 10B: 9C: 8D: 7
参考答案: D 本题解释:正确答案是D考点趣味数学问题解析80÷12=6……8,6条船不够,至少7条。故正确答案为D。
62、有100人参加运动会的三个项目,每人至少参加一项,其中未参加跳远的有50人,未参加跳高的有60人,未参加赛跑的有70人,问至少有多少人参加了不只一项活动?_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析由题意可知,参加跳远的有50人,参加跳高的有40人,参加赛跑的有30人;要使得参加不止一项的人数最少,那么重复参加的人全部都是参加3个项目的。50+40+30-100=20人次,因为重复参加的人都是3个项目,所以被重复计算了2次,则多出的人数是这部分人实际人数的2倍,可得20÷2=10人。故正确答案为B。
63、乘火车从甲城到乙城,1998年初需要19.5小时,1998年火车第一次提速30%,1999年第二次提速25%,2000年第三次提速20%。经过三次提速后,从甲城到乙城乘火车只需要_____。
A: 8.19小时B: 10小时C: 14.63小时D: 15小时
参考答案: B 本题解释:正确答案是B考点行程问题解析设1998年火车的速度为v,三次提速后所需时间为t,三次提速后速度为(1+30%)×(1+25%)×(1+20%)vt=19.5v,解得t=10。因此正确答案为B。
64、某高校对一些学生进行问卷调查。在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120B: 144C: 177D: 192
参考答案: A 本题解释:【解析】A。设参加人数为N,列等式:63+89+47-46-2*24=N-15,N=120。
65、将自然数1-100分别写在完全相同的100张卡片上,然后打乱卡片,先后随机取出4张,问这4张先后取出的卡片上的数字呈增序的几率是多少?_____
A: 1/16B: 1/24C: 1/32D: 1/72
参考答案: B 本题解释:正确答案是B考点概率问题解析
66、一个长方形的长和宽都是质数,并且周长为36米,问这个长方形的面积至多多少平方米?_____
A: 77B: 75C: 60D: 65
参考答案: A 本题解释:参考答案:A题目详解:周长为36米,即长+宽: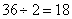 ;将18表示成两个质数合:
;将18表示成两个质数合: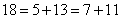 ;分别计算:
;分别计算: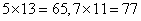 ;
; ;所以,A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
;所以,A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
67、某单位职工24人中,有女性11人,已婚的16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人? _____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释: 【答案】B。解析:易知该单位有男性13人,其中已婚的有10人,故未婚的有3人,选B。
68、已知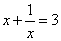 ,则
,则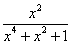 的值为:_____
的值为:_____
A: 9B: 8C: 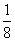 D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:原式的倒数为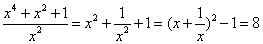 ;则原式=
;则原式= 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
69、某高校对一些学生进行问卷调查。在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120B: 144C: 177D: 192
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析假设只参加一种考试的有X人,则可知:X+46×2+24×3=63+89+47,可知X=35,因此接受调查的学生共有35+46+24+15=120人。故正确答案为A。注:将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体,以A、B、C表示三个集合,以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分,则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。
70、某车工计划15天里加工420个零件,最初3天中每天加工24个,以后每天至少要加工多少个才能在规定的时间内超额完成任务?_____
A: 31B: 29C: 30D: 28
参考答案: B 本题解释:【解析】B。(420-24×3)÷(15-3)=29
71、旅行社对120人的调查显示,喜欢爬山的与不喜欢爬山的人数比为5:3;喜欢游泳的与不喜欢游泳的人数比为7:5;两种活动都喜欢的有43人。对这两种活动都不喜欢的人数是_____。
A: 18B: 27C: 28D: 32
参考答案: A 本题解释:【答案】A。解析:依题意喜欢爬山的有75人,喜欢游泳的有70人,由容斥原理公式,两种活动都不喜欢的有120-(75+70-43)=18人。
72、要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要多少分钟完成?_____
A: 10B: 15C: 16D: 18
参考答案: D 本题解释:答案:D【解析】此题实质上是一道工程问题。设纸飞机总量为1,则甲甲每分钟完成1/30,乙每分钟完成1/45,甲乙共花时间为1/(1/30+1/45)=18。故正确答案应为选项D。
73、足球比赛的记分规则为:胜一场得3分,平1场得1分,输1场得0分。一支足球队要比赛14场,现已比赛了8场,输了一场,得了17分,请问前8场比赛中这支球队赢了几场?_____
A: 7B: 6C: 5D: 4
参考答案: C 本题解释:参考答案:C题目详解:设在前8场比赛中赢了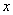 场,则平了
场,则平了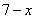 场,则有:
场,则有: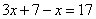 ,解得,
,解得, .所以,选C考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>其他不定方程
.所以,选C考查点:数量关系>数学运算>计算问题之算式计算>不定方程问题>其他不定方程
74、地铁工程在某1000米路段地下施工,两头并进,一侧地铁盾沟机施工,每天掘进3米,工作5天,休息一天进行检修;另一侧工人轮岗不休,每天掘进1米,多少天此段打通_____
A: 282B: 285C: 286D: 288
参考答案: C 本题解释:【答案】C。解析:一侧工程队6天挖3×5=15米,另一侧工程队6天挖6米,以6天为一个周期,两个工程队一个周期一共挖了21米,1000米的路段一共需要1000÷21=47…13。一共需要47个整周期,还余13米,两侧工程队一起挖还需要4天,所以一共需要47×6+4=286天。
75、两个不同的圆最多可以有两个交点,那么三个不同的圆最多可以有几个交点?_____
A: 5个B: 6个C: 7个D: 8个
参考答案: B 本题解释:正确答案是B解析两个圆相交最多有两个交点,第三个圆与这两个圆分别相交最多增加4个交点,所以最多有6个交点,故正确答案为B。几何问题
76、小蔡去超市购物,她买了1.6千克苹果、4磅食油和3.8斤芦柑。请问小蔡买的这三种食品最重的是哪一中?_____
A: 苹果B: 食油C: 芦柑D: 三者一样重
参考答案: C 本题解释:参考答案:C题目详解:同时考查运算和单位换算: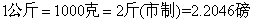 。换算可以得到:小蔡买了约1.814千克食油和1.9千克芦柑;比较1.6、1.814、1.9大小:即可判断出三种食品中芦柑最重;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
。换算可以得到:小蔡买了约1.814千克食油和1.9千克芦柑;比较1.6、1.814、1.9大小:即可判断出三种食品中芦柑最重;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
77、(2009黑龙江)甲、乙两人从两地出发相向而行,他们在相遇后继续前行。当甲走完全程的70%时,乙正好走完全程的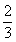 ,此时两人相距220米,问两地相距多少米?_____
,此时两人相距220米,问两地相距多少米?_____
A: 3360米B: 6圈C: 3320米D: 6圈340米
参考答案: B 本题解释:参考答案 题目详解:甲、乙第一次相遇时共跑0.5圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,一圈是2×240=480米。第一次相遇时甲跑了240-100=140米,以后每次相遇甲又跑了140×2=280米,所以第十二次相遇时甲共跑了140+280×11=3220=6圈340米。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
题目详解:甲、乙第一次相遇时共跑0.5圈,乙跑了100米;第二次相遇时,甲、乙共跑1.5圈,则乙跑了100×3=300米,此时甲差60米跑一圈,则可得0.5圈是300-60=240米,一圈是2×240=480米。第一次相遇时甲跑了240-100=140米,以后每次相遇甲又跑了140×2=280米,所以第十二次相遇时甲共跑了140+280×11=3220=6圈340米。考查点:数量关系>数学运算>行程问题>相遇问题>环线相遇问题>环线多次相遇问题
78、由1、2、3、4四个数字组成的四位数共有24个,将它们从小到大排列起来,第18个数是以下哪项?_____
A: 3241B: 3421C: 3412D: 3214
参考答案: B 本题解释:正确答案是B考点排列组合问题解析
79、(2009河北选调,第59题)星期天,小明的妈妈要做下列事情:擦玻璃要20分钟,收拾厨房要15分钟,拖地要15分钟,洗脏衣服的领子、袖口要10分钟,打开全自动洗衣机洗衣服要40分钟,晾衣服要10分钟,干完所有这些事情至少需要多少分钟?_____
A: 110B: 95C: 70D: 60
参考答案: C 本题解释:参考答案:C题目详解:如果按照题目告诉的几件事,一件一件去做,要95分钟。要想节约时间,就要想想在哪段时间里闲着,能否利用闲着的时间做其它事。最合理的安排是:先洗脏衣服的领子和袖口,接着打开全自动洗衣机洗衣服,在洗衣服的40分钟内擦玻璃、拖地和收拾厨房,最后晾衣服,共需70分钟。10+40+10+10考查点:数量关系>数学运算>统筹问题>时间统筹问题
80、某市对52种建筑防水卷材产品进行质量抽检,其中有8种产品的低温柔度不合格,10种产品的可溶物含量不达标,9种产品的接缝剪切性能不合格,同时两项不合格的有7种,有1种产品这三项都不合格,则三项全部合格的建筑防水卷材产品有多少种?_____
A: 37B: 36C: 35D: 34
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析本题注意按照不合格得到三个类,进行容斥原理分析。分别设三项全部合格、仅一项不合格的产品有A、B种,根据题意可得B+7+1=52-A,3×1+2×7+1×B=8+10+9,解得A=34,B=10。故正确答案为D。公式:三集合容斥原理中,将只符合一个条件、只符合两个条件和三个条件都符合的分别看做三个整体,以A、B、C表示三个集合,以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分,则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z成立。标签整体考虑公式应用
81、规定:a※b=(b+a)×b,那么(2※3)※5=_____。
A: 100B: 125C: 300D: 115
参考答案: A 本题解释:参考答案:A题目详解:根据题意,分布计算:2※3=(3+2)×3=15;则原式=15※5=(5+15)×5=100。所以,选A考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
82、某篮球比赛14:00开始,13:30允许观众入场,但早有人来排队等候入场,假设从第一个观众来到时起,每分钟来的观众人数一样多,如果开3个入场口,13:45时就不再有人排队,如果开4个入场口,13:40就没有人排队,那么第一个观众到达的时间是:_____
A: 13:00B: 13:05C: 13:10D: 13:15
参考答案: A 本题解释:【答案】A。解析:设每个入场口每分钟可以进1人,则每分钟到达的观众为(3×15-4×10)÷(15-10)=1,到13:45时,总共有45人入场,需要45分钟,则第一个观众到达时间为13:00。
83、A、B两位同学参加同一次竞赛考试,如果A答对的题目占题目总数的3/4,B答对了25道题,他们两人都答对的题目占题目总数的2/3,那么两人都没有答对的题目共有_____。
A: 5道B: 6道C: 7道D: 8道
参考答案: D 本题解释:参考答案 题目详解:设总题数位x,两人都没答对的题目为y:
题目详解:设总题数位x,两人都没答对的题目为y: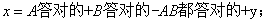
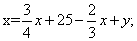 解得,
解得, 又因为,x是12的倍数,
又因为,x是12的倍数, 在这个区间上,唯一的12的倍数是36;所以,
在这个区间上,唯一的12的倍数是36;所以,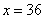 时,
时,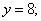 所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
84、某工程甲单独做50天可以完成,乙单独做75天可以完成;现在两人合作,但途中乙因事离开了几天,最后一共花了40天把这项工程做完,则乙中途离开了_____天。
A: 15B: 16C: 22D: 25
参考答案: D 本题解释:参考答案 题目详解:根据题意,设整个工程总量为“1”,则有:乙中途离开,但是甲从始至终工作了40天,那么甲的工作量为:
题目详解:根据题意,设整个工程总量为“1”,则有:乙中途离开,但是甲从始至终工作了40天,那么甲的工作量为: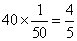 ;该工程中乙需要做的工作量为:
;该工程中乙需要做的工作量为: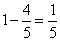 ;乙需要用了
;乙需要用了 天完成;故乙离开了
天完成;故乙离开了 天。所以,选D考查点:数量关系>数学运算>工程问题>合作完工问题
天。所以,选D考查点:数量关系>数学运算>工程问题>合作完工问题
85、将所有自然数,自1开始依次写下去得到:12345678910111213……,试确定第206788个位置上出现的数字_____。
A: 3B: 0C: 7D: 4
参考答案: C 本题解释:【答案】C。解析:一位数占l×9=9个位置,二位数占2×90=180个位置,三位数占3×900=2700个位置,四位数占4×9000=36000个位置,还剩:206788-9-180-2700-36000=167899,167899÷5=33579……4,所以答案为33579+10000=43579的第4个数字7。故应选C。
86、有62名学生,会击剑的有11人,会游泳的有56人,两种都不会的有4人,问两种都会的学生有多少人?_____
A: 1人B: 5人C: 7人D: 9人
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析由两集合容斥原理公式得两种都会的有56+11-(62-4)=9人。故正确答案为D。两集合容斥原理公式:|A∪B|=|A|+|B|﹣|A∩B|。标签两集合容斥原理公式
87、有一架天平,只有5克和30克的砝码各一个。现在要用这架天平把300克味精分成3等份,那么至少需要称多少次?_____
A: 3次B: 4次C: 5次D: 6次
参考答案: A 本题解释:正确答案是A考点统筹规划问题解析第一步,在天平左侧放入30克砝码,然后将300克味精分别放入左右两侧使天平平衡,此时左侧有味精330÷2-30=135克;第二步,用5克和30克砝码称出135克中的35克,则此时还剩100克;第三步,利用称出的100克味精当作砝码再称出100克,此时已将300克味精分成3等份,故正确答案为A。标签分类分步
88、有一项工程含A、B、C、D、E、F六道工序,每道工序分别需要2天、3天、2天、5天、4天、1天时间完成,其中,(1)工序A、B第一天就可以同时动工;(2)工序C必须在工序A、B都完成后才可以动工;(3)工序D必须在工序C完成后才可以动工;(4)工序E必须在工序C完成后才可以动工;(5)工序F必须在工序D、E都完成后才可以动工。那么,完成这项工程至少需要多少天?_____
A: 10B: 11C: 12D: 13
参考答案: B 本题解释:参考答案:B题目详解:A、B第一天同时动工,A、B都完成需3天。C第四天动工,完成需2天。D、E第六天同时动工,D、E都完成需要5天。F第十一天动工,完成需1天,故完成工程至少需要 天.考查点:数量关系>数学运算>统筹问题>时间统筹问题
天.考查点:数量关系>数学运算>统筹问题>时间统筹问题
89、某小区物业征集业主意见,计划从100户业主中抽取有20户进行调查。100户业主中有b户主年龄超过60岁,a户户主年龄不满35岁,户主年龄在36岁到59岁的有25户。为了使意见更具代表性,物业采取分层抽样的方法,从b户中抽取了4户,则a的值可能是_____。
A: 55B: 66C: 44D: 50
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析100户中抽取20户,可知抽取比例为5:1,根据题意,4:b=20:100,a+b=75,解得a=55。故答案为A。
90、毛毛骑在牛背上过河,他共有甲、乙、丙、丁4头牛,甲过河要2分钟,乙过河要3分钟,丙过河要4分钟,丁过河要5分钟。毛毛每次只能赶2头牛过河,要把4头牛都赶到对岸去,最少要多少分钟? _____
A: 16B: 17C: 18D: 19
参考答案: A 本题解释:A。若要时间最短,则一定要让耗时最长的两头牛同时过河。先骑甲、乙过河,骑甲返回,共用5分钟;再骑丙、丁过河,骑乙返回,共用8分钟;最后再骑甲、乙过河,用3分钟,共用时5+8+3=16分钟。
91、某服装店老板去采购一批商品,其所带的钱如果只买某种进口上衣可买120件,如果只买某种普通上衣则可买180件。现在知道,最后该老板买的进口上衣和普通上衣的数量相同,问他最多可以各买多少件?_____
A: 70件B: 72件C: 74件D: 75件
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析根据题意,设钱数为360元,则进口上衣3元,普通上衣2元,因此可以各买360÷(3+2)=72件。
92、某商场举行周年让利活动,单件商品满300返180元,满200返100元,满100返40元,如果不参加返现金的活动,则商品可以打5.5折。小王买了价值360元、220元、150元的商品各一件,问最少需要多少钱?_____
A: 401.5元B: 410元C: 360元D: 382.5元
参考答案: D 本题解释:正确答案是D考点经济利润问题解析如果打折,则买360元的产品只需360×0.55>360-180=180,所以采用满300返180元更好;打折买220元的产品只需220×0.55=121>220-100=120,采用满200返100元更好;买150元的产品,打折只需150×0.55=82.5元,采用打折更好;所以最少需要180+120+82.5=382.5元。故正确答案为D。
93、二十几个小朋友围成一圈,按顺时针方向一圈一圈地连续报数。如果报2和200的是同一个人,那么共有_____个小朋友。
A: 22B: 24C: 27D: 28
参考答案: A 本题解释:A【解析】小朋友的人数应是(200-2)=198的约数,而198=2×3×3×11。约数中只有2×11=22符合题意。
94、(2009山东,第120题)先分多次用等量清水去冲洗一件衣服,每次均可冲洗掉上次所残留污垢的四分之三,则至少需要多少次才可使得最终残留的污垢不超过初始污垢的 ?_____
?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:参考答案:B题目详解:解法一:每次清洗之后变为原来的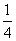 ,那么
,那么 次之后就应该是原来的
次之后就应该是原来的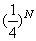 ,由题意:
,由题意: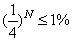 ,即
,即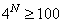 ,易知
,易知 。解法二:第一次冲洗冲洗掉
。解法二:第一次冲洗冲洗掉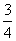 ,原污垢剩下
,原污垢剩下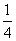 第二次冲洗原污垢的
第二次冲洗原污垢的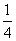 又被洗去了
又被洗去了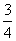 ,剩下
,剩下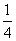 的
的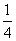 ,即
,即 以此类推第三次
以此类推第三次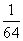 第四次冲洗,所剩下污垢就小于百分之一了。选B考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
第四次冲洗,所剩下污垢就小于百分之一了。选B考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
95、一批树苗有100多棵,小王每天种8棵,第21天种完,小李每天种9棵,第18天种完。小孙每天种10棵,问第几天可以种完?_____
A: 14B: 15C: 17D: 18
参考答案: C 本题解释:【答案】C。解析:设这批树苗一共有z棵,从“小王每天种8棵,第21天种完”可知,8×20+l≤z≤8×21;从“小李每天种9棵,第18天种完”可知,9×17+1≤z≤9×18,结合两个不等式得:161≤z≤162。如果小孙每天种10棵的话,在z的取值范围内,一定是在第17天种完。
96、某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师,培训中心将所有的钢琴学员和拉丁舞学员共76人分剐平均地分给各个老师带领,刚好能够分完,且每位老师所带的学生数量都是质数。后来由于学生人数减少,培训中心只保留了4名钢琴教师和3名拉丁舞教师,但每名教师所带的学生数量不变,那么目前培训中心还剩下学员多少人?_____
A: 36B: 37C: 39D: 41
参考答案: D 本题解释:正确答案是D考点函数最值问题解析假定每个钢琴教师带x个学生,每个拉丁舞教师带y个学生,则根据题意有:5x+6y=76。根据此方程,可知x必为偶数,而x与y均为质数,因此x=2,代回可得y=11。于是在学生人数减少后,还剩下学员为4×2+3×11=41个,故正确答案为D。标签数字特性
97、一项工程,甲单独做,6天可完成;甲乙合做,2天可完成;则乙单独做,_____天可完成。
A: 1.5 B: 3 C: 4 D: 5
参考答案: B 本题解释: B。设这项工程为单位1,则甲的速度为吉,甲乙共同速度为1/2么乙的速度为1/2-1/6-1/3则乙做完这项工程需要3天。故正确答案为B。
98、林文前年买了8000元的国家建设债券,定期3年。到期他取回本金和利息一共10284.8元。这种建设债券的年利率是多少?_____
A: 9.52%B: 9.6%C: 8.4%D: 9.25%
参考答案: A 本题解释:A。【解析】求利息的公式:利息=本金×利率×时间,可得出:利率=利息÷时间÷本金。而他3年所得的利息是:10284.8-8000=2284.8(元);这样即可求出这债券的年利率是多少。(10284.8-8000)÷3÷8000=2284.8÷3÷8000=761.6÷8000=0.0952=9.52%。
99、如图,圆拱桥的拱高BD=2m,跨度AC=8m,可以计算圆拱的半径是_____。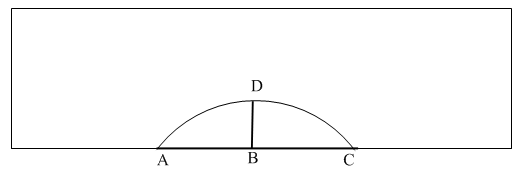
A: 5mB: 10mC: 12mD: 17m
参考答案: A 本题解释:正确答案是A考点几何问题解析设半径为R,根据勾股定理,则有R×R-(R-2)×(R-2)=4×4,解得R=5,故正确答案为A。
100、一条船往返于甲、乙两港之间,由甲至乙是顺水行驶,由乙至甲是逆水行驶。已知船在静水中的速度为8千米/时,平时逆行与顺行所用的时间比为 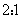 。某天恰逢暴雨,水流速度为原来的2倍,这条船往返共用9小时问:甲、乙两港相距多少千米?_____
。某天恰逢暴雨,水流速度为原来的2倍,这条船往返共用9小时问:甲、乙两港相距多少千米?_____
A: 24B: 20C: 16D: 32
参考答案: B 本题解释:参考答案:.B题目详解:根据题意,设水流的速度是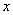 千米/时,甲乙两港之间的距离是
千米/时,甲乙两港之间的距离是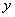 千米,则有:顺水速度=船速+水速
千米,则有:顺水速度=船速+水速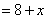 ;逆水速度=船速-水速
;逆水速度=船速-水速 ;而速度之比等于时间比的倒数;于是
;而速度之比等于时间比的倒数;于是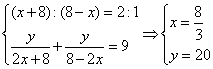 所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
所以,选B。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题