1、市A公路收费站，去年的收费额比今年的收费额少1/5，估计明年收费额比今年的收费额多1/6，那么明年的收费额估计要比去年的收费额多几分之几？_____
A: 11/24B: 11/25C: 11/30D: 11/60
参考答案: A 本题解释:A。设今年30，则去年是24，明年是35，则明年比去年多了（35-24）/24=11/24，选A。

2、商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达，女孩用50秒钟到达。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 80级 B: 100级 C: 120级 D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80，女孩所走的台阶数为50/2×3=75，那么电梯的速度就应该为（80-75）/（50-40）=0.5，电梯所经过的台阶就为40×0.5=20， 电梯经过的台阶加上男孩经过的台阶，就是电梯的台阶数，即100级。

3、孙儿孙女的平均年龄是10岁，孙儿年龄的平方减去孙女年龄的平方所得的数值，正好是爷爷出生年份的后两位，爷爷生于上个世纪40年代。问孙儿孙女的年龄差是多少岁?_____
A: 2B: 4C: 6D: 8
参考答案: A 本题解释:代入排除思想。代入A项，若相差2岁，则孙儿孙女分别为9岁和11岁，11×11-9×9=40，满足题意。

4、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+（-7）=-12。故本题选C。

5、定义：①群体互补效应：由不同年龄、专业、智能水平、气质类型的人才有机地组成一个结构合理的人才群体，达到知识互用、能力互补，使只有专才的个体，变成多能的人才群。②群体协调效应：在结构合理的人才群体中，逐步形成了群体每个成员共同遵守的良好的道德规范和传统作风，以此调节和协调群体中个体与个体、个体与群体、群众与社会的关系，并影响和控制整个群体，使群体的力量和功能得到维护和加强。③群体感应效应：在结构合理的人才群体中，人才之间在目标上志同道合，在学风上互相感染，在学术上互相影响，同心同德，紧密团结，创新意识和创造思维不断激化和强化，形成对人才创造特别有利的“微型气候”。典型例证：(1)某大学有效整合资源，在校内外组织多方面人才，团结协作，集体攻关。(2)正因为好大学有优良的校风和传统，所以人人才都想上好大学。(3)小李做事低调，从不张扬。上述典型例证与定义存在对应关系的数目有_____。
A: 0个B: 1个C: 2个D: 3个
参考答案: C 本题解释:【答案】C。解析：第一步：抓住每个定义中的关键词群体互补效应：关键词强调“不同年龄、专业、智能水平、气质类型的人才”、“知识互用、能力互补”。群体协调效应：关键词强调“群体每个成员共同遵守”、“调节和协调”。群体感应效应：关键词强调“目标上志同道合，在学风上互相感染，在学术上互相影响”。第二步：逐一分析例证与定义间的关系例证（1）大学组织了多方面的人才，形成群体互补效应，对应定义①，例证（2）好大学因为有优良的校风和传统而受欢迎，属于群体感应效应，对应定义③；例证（3）讲的是小李的个体行为，与上面的定义均不相符。例证与定义存在对应关系的数目有2个，故正确答案为C。

6、小龙、小虎、小方和小圆四个孩子共有45个球，但不知道每个人各有几个球，如果变动，一下，小龙的球减少2个，小虎的球增加2个，小方的球增加一倍，小圆的球减少一半，那么四个人球的个数就一样多了。原来小虎有_____个球。
A: 12B: 5C: 8D: 20
参考答案: C 本题解释:【解析】设四个人的球数在变动后的个数为χ，可得方程（χ+2）+（χ-2）十2χ+0.5χ=45，解得χ=10，则原来小虎有10-2=8个球。

7、某商场开展购物优惠活动：一次购买300元及以下的商品九折优惠;一次购买超过300元的商品，其中300元九折优惠，超过300元的部分八折优惠。小王购物第一次付款144元，第二次又付款310元。如果他―次购买并付款，可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:A【解析】统筹优化问题。由题意，第一次付款144元可得商品原价为160元;第二次付款为310元，可得原价为350元。故总价510元，按照优惠，需付款300×0.9+210×0.8=438元，节省了454-438=16元。

8、建华中学共有1600名学生，其中喜欢乒乓球的有1180人，喜欢羽毛球的有1360人，喜欢篮球的有1250人，喜欢足球的有1040人，问以上四项球类运动都喜欢的至少有几人？_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析：采取逆向思维法。不喜欢乒乓的1600－1180＝420，不喜欢羽毛球的1600－1360＝240，不喜欢篮球的1600－1250＝350，不喜欢足球的1600－1040＝560，要使四项运动都喜欢的人数最少，那么不喜欢的人数就要最多那么都尽量不相交，从而达到最多：420＋240＋350＋560＝1570人，所以喜欢的最少的为1600－1570＝30人，故正确答案为B。

9、某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票?_____
A: 382位B: 406位C: 451位D: 516位
参考答案: B 本题解释:【答案】B。解析：从10位候选人中选2人共有种票，则每种票有9张相同时需要×9=405个

10、一个工人加工一批产品，他每加工出一件正品，得报酬0.75元，每加工出一件次品，罚款1.50元。这天他加工的正品是次品的7倍，得款11.25元。那么他这天加工出多少件次品?_____
A: 1B: 3C: 7D: 13
参考答案: B 本题解释:B【解析】 工人加工7件正品得款0.75×7=5.25（元），加工出一件次品罚款1.50元，所以每加工8件产品得款5.25-1.50=3.75（元）。所以他这天加工出的次品是11.25÷3.75=3（件）。

11、某年级有84名学生，其中男生的年龄之和是女生的3倍。3年后，男生的年龄之和比女生年龄之和的3倍少36岁。问该年级男生有多少人?_____
A: 48B: 54C: 60D: 66
参考答案: C 本题解释:【答案解析】若男生人数为女生人数的3倍，则3年后，男生的年龄之和仍然为女生的3倍。3年后男生年龄之和比女生年龄之和的3倍少36岁，说明男生人数比女生人数的3倍少36÷3=12人，故女生人数为(84+12)÷(3+1)=24人，男生为84-24=60人。

12、某工厂有学徒工、熟练工、技师共80名，每天完成480件产品的任务。已知每天学徒工完成2件，熟练工完成6件，技师完成7件，且学徒工和熟练工完成的量相等，则该厂技师人数是熟练工人数的_____倍。
A: 6B: 8C: 10D: 12
参考答案: D 本题解释:列方程组。设学徒工、熟练工、技师分别有x，y，z名。则有：X+Y+Z=80，2X-96Y+7Z=48012X=6Y得到：X=15，y=5，Z=60，所以Z：Y=60：5=12。选D。

13、某篮球比赛14:00开始，13:30允许观众入场，但早有人来排队等候入场，假设从第一个观众来到时起，每分钟来的观众人数一样多，如果开3个入场口，13:45时就不再有人排队，如果开4个入场口，13:40就没有人排队，那么第一个观众到达的时间是：_____
A: 13:00B: 13:05C: 13:10D: 13:15
参考答案: A 本题解释:【答案】A。解析：设每个入场口每分钟可以进1人，则每分钟到达的观众为（3×15-4×10）÷（15-10）=1，到13:45时，总共有45人入场，需要45分钟，则第一个观众到达时间为13:00。

14、如是2003除以一个两位数后，所得余数最大，则这个两位数为_____。
A: 92B: 82C: 88D: 96
参考答案: D 本题解释:D【解析】 2003÷99=20……2323+20×3=83所以商是20时，余数最大是83，此时除数是99-3=96。2003÷95=21……88+21×3=71所以商是21时，余数最大是71，此时除数是95-3=92。2003÷91=22……11+22×3=67所以商是22时，余数最大是67，此时除数是91-3=88。2003÷87=23……22+23×3=71所以商是23时，余数最大是71，此时除数是87-3=84。当除数小于84时，余数小于83。综上所述，余数最大是83，此时除数AB=96。

15、一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队，每个人都与其余九名选手各赛一盘，每盘棋的胜利者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，那么甲、乙、丙三队参加比赛的选手的人数依次是_____。
A: 6人、3人、1人B: 4人、5人、1人C: 3人、5人、2人D: 5人、1人、4人
参考答案: B 本题解释:B【解析】根据10名选手参加比赛，取胜者得1分，而丙队选手平均得分9分，这样丙队参赛选手只能是1人，且与其余9名选手比赛中应全部获胜。又根据每盘赛棋中胜者得1分，负者0分，平局各得0.5分，可知各队得分总数应是整数或小数部分的十位上是5，现乙队选手平均得3.6分，十位上是6，同样，甲、乙两队共有9人参赛，这样乙队参赛选手肯定是5人。因此甲队参赛选手人数是4人，乙队参赛选手人数是5人，丙队参赛选手人数是1人。

16、某条道路的一侧种植了51棵梧桐树，其中道路两端各有一棵，且相邻两棵树之间的距离相等。如果需要在这一侧再多种10棵树，且通过移动一部分树(不含首尾两棵)使所有相邻两棵树之间的距离仍然相等，则这51棵树中至少有多少棵不需要移动位置？_____
A: 9B: 10C: 11D: 12
参考答案: C 本题解释:【答案】C。解析：设路长为50×60米，则第一次的间距为60米，第二次的间距为50米，不需要移动位置的树距起点的距离必须为60和50的公倍数，即距离应是300的倍数。总长为3000米，则中间有9棵树不需要移动，再加上首尾两棵，一共有11棵树不需要移动。因此，本题选择C选项。

17、某小学五年级同学分成69个小组，每组3人，去参加植树劳动。在这些小组中，只有1名男同学的共有15个小组，至少有2名女同学的共有36个小组，有3名男同学的小组与有3名女同学的小组同样多。问这所小学五年级共有男同学多少名?_____
A: 102B: 136C: 144D: 158
参考答案: A 本题解释:【解析】A。有1名男生2名女生的小组有15个，则有3名女生的小组有36-15=21个，所以有3名男生的小组也有21个，只有1名女生的小组有69-15-21-21=12个，故男生一共有15+12×2+21×3=102名。

18、由1、2、3组成的没有重复数字的所有三位数之和为多少？_____
A: 1222 B: 1232 C: 1322 D: 1332
参考答案: D 本题解释:D。因为1、2、3之和可被3整除，故而1、2、3所组成的没有重复数字的三位数都能被3整除，而这些数字相加之和也必能被3整除，只有D项能被3整除，为正确答案。根据排列组合原理，可知该没有重复数字的三位数共有6个，1、2、3三个数在个、十、百位上各出现两次，即（1+2+3）×2=12，也就是说这一数字当为12+120+1200=1332。

19、某社团共有46人，其中36人爱好戏剧，30人爱好体育，38人爱好写作，40人爱好收藏，问这个社团至少有_____人以上四项活动都喜欢。
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:【答案解析】根据题意可知，不爱好戏剧的有46-36=10人，不爱好体育的有46-30=16人，不爱好写作的有46-38=8人，不爱好收藏的有46-40=6人。要使四项活动都喜欢的人最少，则应使不爱好这四项活动的人最多，即使不爱好这四项活动的人均不重复，所以至少有46-(10+16+8+6)=6人四项活动都喜欢。所以正确答案为B项。

20、某项工程计划300天完成，开工100天后，由于施工人员减少，工作效率下降20%，问完成该工程比原计划推迟多少天? _____
A: 40B: 50C: 60D: 70
参考答案: B 本题解释: B。根据效率与时间成反比，可得正常200天的工作，效率下降后需要200÷ （1-20%） =250天，故需推迟50天。

21、2004×(2.3×47+2.4)÷(2.4×47-2.3)的值为_____。
A: 2003B: 2004C: 2005D: 2006
参考答案: B 本题解释:B【解析】原式=2004×[（2.4-0.1）×47+2.4]÷（2.4×47-2.3）=2004×（2.4×47-4.7+2.4）÷（2.4×47-2.3）=2004×（2.4×47-2.3）÷（2.4×47-2.3）=2004

22、从12时到13时，钟的时针与分针可成直角的机会有_____。
A: 1次B: 2次C: 3次D: 4次
参考答案: B 本题解释:【答案解析】一个小时内成直角只有两次，选B。

23、小张与小王分别从甲、乙两村同时出发，在两村之间往返行走(到达另一村后就马上返回)，他们在离甲村3.5千米处第一次相遇，在离乙村2千米处第二次相遇。问他们两人第四次相遇的地点离乙村多远(相遇指迎面相遇)？_____
A: 1千米 B: 1.2千米C: 1.5千米D: 1.8千米
参考答案: A 本题解释:【答案】A。解析：直线多次相遇问题。第二次相遇两人已共同走了甲、乙两村距离的3倍，因此张走了3.5×3＝10.5千米。从图上可看出，第二次相遇处离乙村2千米，因此，甲、乙两村距离是10.5-2＝8.5千米。每次相遇甲乙二人路程和都比上次相遇多2倍的两地间距。第四次相遇时，两人已共同走了（3＋2＋2）倍的两村距离，其中张走了3.5×（2×4-1）＝24.5千米，24.5=8.5＋8.5＋7.5千米。因此第四次相遇处，离乙村8.5-7.5=1千米。

24、某学校入学考试，确定了录取分数线。在报考的学生中，只有1/3被录取，录取者平均分比录取分数线高6分，没有被录取的学生其平均分比录取分数线低15分，所有考生的平均分是80分，推知录取分数线是_____。
A: 80B: 84C: 88D: 90
参考答案: C 本题解释:【答案】C。解析：不难看出，总共有多少人参加考试对本题的最终结果没有影响，仅是录取分数线的1/3对结果有影响，也即最后结果只与这个比例有关，而与总数无关。那么就可以直接看做录取了1个人，有2个人没录取，总人数为3人，则假定录取分数线为x分，于是得方程：（x﹢6）﹢（x－15）×2＝80×3，解得x＝88。故正确答案为C。

25、从一张1952mm×568mm的长方形纸片上，剪下一个边长尽可能大的正方形，如果剩下的部分不是正方形，那么在剩下的纸片上再剪下一个边长尽可能大的正方形。按照上面的过程不断地重复，最后一共可剪得正方形多少个？_____
A: 8B: 10C: 12D: 14
参考答案: D 本题解释:从长1952mm、宽568mm的长方形纸片上首先可剪下边长为568mm的正方形，这样的正方形的个数恰好是1952除以568所得的商，而余数恰好是剩下的长方形的宽，于是有：1952÷568=3…248，568÷248=2…72，248÷72=3…32，72÷32=2…8，32÷8=4，因此一共可得到正方形3+2+3+2+4=14（个），故正确答案为D。

26、有一个数，除以3余数是2，除以4余数是1。问这个数除以12余数是几?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:B【解析】设这个数除以12，余数是a。那么a除以3，余数是2;a除以4，余数是1。而在0，1，2，…，11中，符合这样条件的a只有5，故这个数除以12余5。

27、有一本畅销书，今年每册书的成本比去年增加了10%，因此每册书的利润下降了20%，但是今年的销量比去年增加了70%。则今年销售该畅销书的总利润比去年增加了_____。
A: 36%B: 25%C: 20%D: 15%
参考答案: A 本题解释:每本书的利润值下降了20%，为原来的0.8，销量增加了70%，为原来的1.7，1.7×0.8=1.36，1.36—1=0.36，即为36%。

28、有一段布，裁剪制服6套多12尺，若裁剪8套则缺8尺，则这段布是_____尺。
A: 36B: 72C: 144D: 288
参考答案: B 本题解释:B在本题中宜用列方程法来求解，设每套衣服需用布料x尺，则依题有6x+12=8x-8，解之得x=10，故这段布长为6×10+12=72（尺），正确答案为B。

29、现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。若从甲中取2100克，乙中取700克混合而成的消毒浓度为3%；若从甲中取900克，乙中取2700克，则混合而成的溶液的浓度为5%。则甲、乙两种消毒溶液的浓度分别为_____。
A: 3%6%B: 3%4%C: 2%6%D: 4%6%
参考答案: C 本题解释:【答案】C。解析：设两种溶液的浓度分别为a、b，则可列方程2100a＋700b＝（2100＋700）×3%，900a＋2700b＝（900＋2700）×5%，解得a=2%，仅C选项符合，故正确答案为C。老师点睛:甲中去2100克，乙中取700克混合而成的消毒溶液浓度为3%，则甲、乙两溶液的浓度必然是一个比3%大，一个比3%小，只有C选项符合，故正确答案为C。

30、某人在雅虎上申请了一个邮箱，邮箱密码是由0至9中任意4个数字组成，他任意输入4个数字，输入正确密码的概率是_____。
A: 10　B: 10　C: 10　D: 10
参考答案: B 本题解释:B[解析]正确的密码只有一个，这10个数字的组合共有10个，所以答案是B。

31、某商场出售甲乙两种不同价格的笔记本电脑，其中甲电脑连续两次提价10%，乙电脑连续两次降价10%，最后两种电脑均以9801元售出各一台，与价格不升不降比较，则商场盈亏情况是_____。
A: 不亏不赚B: 少赚598元C: 多赚980.1元D: 多赚490.05元
参考答案: B 本题解释:【答案】B。解析：由题干可知价格调整之前，乙电脑价格高于甲电脑，则乙电脑两次降价10%降的部分要大于甲电脑两次提价10%的部分，因此调整后两台电脑的总价格小于调价前的价格，从而商场少赚了，故正确答案为B。

32、n为100以内的自然数，那么能令2n-1被7整除的n有多少个?_____
A: 32B: 33C: 34D: 35
参考答案: B 本题解释:答案：B.[解析]当n是3的倍数的时候，2n-1是7的倍数。也就是求100以内3的倍数，从3到99，共有33个。故选B。

33、某月的最后一个星期五是这个月的25号，这个月的第一天是星期几?_____
A: 星期二B: 星期三C: 星期四D: 星期六
参考答案: A 本题解释:A 【解析】因为25=3×7+4，所以这个月的4号也是星期五，故这个月的第一天是星期二。

34、甲、乙、丙、丁四个人比赛打羽毛球，每两个都要赛一场，已知甲胜了丁，并且甲、乙、丙三人胜的场数相同，那么丁胜了几场？_____
A: 6 B: 0 C: 12 D: 3
参考答案: B 本题解释:【解析】B。每人至多赛3场，排除A、C。甲胜丁，则丁至少输1场，排除D。

35、一条街上，一个骑车人和一个步行人相向而行，骑车人的速度是步行人的3倍，每个隔10分钟有一辆公交车超过一个行人。每个隔20分钟有一辆公交车超过一个骑车人，如果公交车从始发站每隔相同的时间发一辆车，那么间隔几分钟发一辆公交车? _____
A: 10 B: 8 C: 6 D: 4
参考答案: B 本题解释:B。【解析】令间隔t，汽车速度b，自行车速度3a，人速a，这道题关键是相对速度乘以相对时间等于路程差。车路程差为b×t，与行人相同方向行驶的汽车的相对速度为b-a，行驶b×t的相对时间为10=>b×t=10×（b-a） 同理，可得b×t=20×（3a-b），通过车路程差为b×t求出a/b=1/5，带入原式t=8。

36、小赵、小钱、小孙一起打羽毛球，每局两人比赛，另一人休息。三人约定每一局的输方下一局休息。结束时算了一下，小赵休息了2局，小钱共打了8局，小孙共打了5局。则参加第9局比赛的是_____。
A: 小钱和小孙B: 小赵和小钱C: 小钱和小孙D: 以上皆有可能
参考答案: B 本题解释:B。本题关键在于三个人打羽毛球，一人休息的时候必然是另外两人比赛的时候。因此条件“小赵休息了2局”，说明小钱和小孙对战了2局，则两人其余的比赛都是和小赵进行的，于是总的比赛局数为8+5-2=11（局）。三人比赛中，任何一个人不可能连续休息两场，也即每个人的休息场次只能是间隔的，而11局比赛中小孙打了5局，休息了6局，那么他只能是这11局比赛中的第2、4、6、8、10局中上场。因此第9局比赛中小孙没有上场，也即参加比赛的是小赵和小钱。故选B。

37、在一个口袋中有l0个黑球、6个白球、4个红球.至少从中取出多少个球才能保证其中有白球? _____
A: 14B: 15C: 17D: 18
参考答案: B 本题解释:【答案】B.解析：抽屉原理，最坏的情况是10个黑球和4个白球都拿出来了，最后第15次拿到的肯定是白球。

38、如下图，梯形ABCD的对角线AC⊥BD，其中AD=1/2，BC=3，AC=2×4/5，BD=2.1。问梯形ABCD的高AE的值是_____。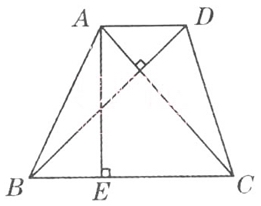
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=（AD+BC）×AE→AE=42/25。

39、在同一环形跑道上小陈比小王跑得慢，两人都按同一方向跑步锻炼时，每隔12分钟相遇一次；若两人速度不变，其中一人按相反方向跑步，则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟？_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:不妨设小王和小陈速度分别为x，y，跑道长度为s，则：两人都按同一方向跑步锻炼时，每隔12分钟相遇一次，说明s/（x—y）=12;若两人速度不变，其中一人按相反方向跑步，则每隔4分钟相遇一次，说明s/（x+y）=4;解得s=6x=12y，所以两人跑完一圈花费的时间小陈比小王多6分钟。

40、小红把平时节省下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是_____。
A: 1元 B: 2元 C: 3元 D: 4元
参考答案: C 本题解释:C。【解析】设三角形每条边X，正方形为Y，那么Y=X-5，同时由于硬币个数相同，那么3X=4Y，如此可以算出X=20，则硬币共有3×20=60个，硬币为5分硬币，那么总价值是5×60=300（分），得出结果。

41、在一条公路旁有4个工厂，每个工厂的人数如图所示，且每两厂之间距离相等。现在要在公路旁设一个车站，使4个工厂的所有人员步行到车站总路程最少，这个车站应设在几号工厂门口?_____
A: 1号B: 2号C: 3号D: 4号
参考答案: C 本题解释:C【解析】 一般情况车站设在几个工厂的中间，即设在2号工厂或3号工厂门口。由于各厂人数不同，还是应通过计算再决定车站在哪一个工厂门口合适。如果设车站建在2号工厂门口，且设每两个工厂之间距离为1千米，那么4个工厂所有人员步行总路程为：1×100+1×80+2×215=100+80+430=610（千米）如果车站设在3号工厂门口，每两个工厂之间的距离为1千米，那么4个工厂所有人员步行总路程为：1×100×2+1×120+1×215=200+120+215=535（千米）显然，车站设在3号厂门口，才能使4个工厂所有人员步行到车站总路程最少。故本题选C。

42、新上任的库房管理员拿着20把钥匙去开20个库房的门，他只知道每把钥匙只能打开其中的一扇门，但不知道哪一把钥匙开哪一扇门，现在要打开所有关闭的20个库房门，他最多要开多少次?_____
A: 80B: 160C: 200D: 210
参考答案: D 本题解释:D【解析】本题应从最不利情况去考虑：打开第一个房间要20次，打开第二个房间要19次……共计要开20+19+18+…+1=210（次）。

43、某书店对顾客有一项优惠，凡购买同种书百册以上，按书价90%收款。某单位到书店购买甲、乙两种书，其中乙种书的册数是甲种书册数的3/5，只有甲种书得到了90%的优惠，这时买甲种书所付总钱数是买乙种书所付总钱数的2倍，已知乙种书每本定价1.5元，那么优惠前甲种书每本原价是_____元。
A: 3B: 2.5C: 2D: 1.5
参考答案: C 本题解释:C【解析】设优惠前甲种书每册定价χ元。设甲种书册数为1，乙种书册数为3/5，则甲种书总价钱为90%χ×1，乙种书总价钱的2倍为1.5×3/5×2，此时有以下相等关系：90%χ=1.5×3/5×2，解得χ=2。即优惠前甲种书每册定价2元。

44、某城市9月平均气温为28.5度，如当月最热日和最冷日的平均气温相差不超过10度，则该月平均气温在30度及以上的日子最多有多少天?_____
A: 24B: 25C: 26D: 27
参考答案: B 本题解释:设该月的日平均气温在30度及以上的日子为2天，要使其最多，则最热日的气温应尽可能地接近30度，故可假设最热日的气温都是30度，最冷日的气温都是20度，根据题意可知，30x+20×（30一x）≤28.5×30→x≤25.5。故选B。

45、甲、乙、丙、丁四人今年分别是16、12、11、9岁。问多少年前，甲、乙的年龄和是丙、丁年龄和的2倍?_____
A: 4B: 6C: 8D: 12
参考答案: B 本题解释: 【解析】B。解法一、设x年前满足条件，则（16-x）+（12-x）=[（11-x）+（9-x）]×2;解法二、两组年龄差为8岁（分别作差5+3=8），当第一组为第二组两倍时肯定是16与8岁。现在第一组和为28岁，需要倒退12岁到16岁，需要6年，因为两个人一年一共倒退2岁。

46、某企业发奖金是根据利润提成的。利润低于或等于10万元时可提成10%,低于或等于20万元时,高于10万元的部分按7.5%提成;高于20万元时,高于20万元的部分按5%提成。当利润额为40万元时,应发放奖金多少万元?_____
A: 2B: 2.75C: 3D: 4.5
参考答案: B 本题解释:【答案】B。解析:40万元的利润,10万元按10%计算利润,10万元按7.5%计算利润,再20万元按5%计算利润。共10×10%+10×7.5%+20×5%=2.75万元。

47、某单位职工24人中，有女性11人，已婚的16人。在已婚的16人中有女性6人。问这个单位的未婚男性有多少人？_____
A: 1B: 3C: 9D: 12
参考答案: B 本题解释:B。易知该单位有男性13人，其中已婚的有10人，故未婚的有3人，选B。

48、两个相同的瓶子装满酒精溶液，一个瓶子中酒精与水的体积比是3:1，另一个瓶子中酒精与水的体积比是4:1，若把两瓶酒精溶液混合，则混合后的酒精和水的体积之比是多少?_____
A: 31:9B: 7:2C: 31:40D: 20:11
参考答案: A 本题解释:【答案解析】(3/4+4/5)/(1/4+1/5)=31：9

49、今年父亲年龄是儿子年龄的10倍，6年后父亲年龄是儿子年龄的4倍，则今年父亲、儿子的年龄分别是_____。
A: 60岁，6岁 B: 50岁，5岁C: 40岁，4岁 D: 30岁，3岁
参考答案: D

50、从1、2、3、4中任取3个数组成没有重复的三位数的偶数的取法种数为_____。
A: 10 　 B: 12 　 C: 13 　 D: 11
参考答案: B 本题解释:【解析】B。 题干要求组成没有重复数字的三位数的偶数，所以只有尾数是2或4两种情况。当尾数是2时，有2×3=6（种）；当尾数是4时，有2×3=6（种），所以共有6+6=12（种），故本题答案为B。

51、甲、乙有数量相同的萝卜，甲打算卖1元2个，乙打算卖1元3个，如甲、乙二人一起按2元5个卖全部的萝卜，总收入会比预想的1个人少4元，两人共有多少萝卜？_____
A: 420B: 120C: 360D: 240
参考答案: D 本题解释:D。

52、一个空的容积为64 升的鼓形圆桶上有A、B 两孔，一种蒸馏水从A 孔流入同 时从B 孔流出，如果通过A 孔的流速为3 升/小时，那么在B 孔的流速为多少升时才能保证用96 小时恰好装满容器?_____
A: 4/3 　 　B: 8/3　 　C: 7/3　 　D: 3/7
参考答案: C 本题解释:【答案】C[解析]从A孔流入同时从B孔流出，设流速X，则容器实际蓄水速度为3-X，所以64/(3-X)=96，求出X=7/3。

53、从一瓶浓度为20%的消毒液中倒出2/5后，加满清水，再倒出2/5，又加满清水，此时消毒液的浓度为：_____
A: 7.2%B: 3.2%C: 5.0%D: 4.8%
参考答案: A

54、某高校对一些学生进行问卷调查。在接受调查的学生中，准备参加注册会计师考试的有63人，准备参加英语六级考试的有89人，准备参加计算机考试的有47人，三种考试都准备参加的有24人，准备选择两种考试都参加的有46人，不参加其中任何一种考试的都15人。问接受调查的学生共有多少人?_____
A: 120B: 144C: 17 91ExaM.org7D: 192
参考答案: A 本题解释:【解析】A。设参加人数为N，列等式：63+89+47-46-2*24=N-15，N=120。

55、某人将一套房屋以购入价的3倍在房产中介处放盘。他告诉中介，一周内签约的买家其成交价能比放盘价再便宜5万元，并愿意支付成交价3%的中介费基础上，再多支付1万元给中介。若该房屋在一周内以100万元的价格成交，那么，此人在这套房屋上盈利_____万
A: 66B: 65C: 61D: 58
参考答案: C 本题解释:【答案】C。解析：成交价100，则据题意放盘价是100+5=105，可知购入价是105÷3=35，中介费是100X3%+1=3+1=4.可知盈利100-35-4=61。因此，本题答案选择C项。

56、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。

57、今年小方父亲的年龄是小方的3倍，去年小方的父亲比小方大26岁，那么小方明年多大?_____
A: 16B: 13C: 15D: 14
参考答案: D 本题解释:去年小方的父亲比小方大26岁，即年龄差为26。今年小方父亲的年龄是小方的3倍，则年龄差是今年小方年龄的2倍，于是今年小方为13岁，因此明年小方14岁。故选D。

58、甲、乙两种商品成本共2000元，商品甲按50％的利润定价，商品乙按40％的利润定价，后来打折销售，两种商品都按定价的80％出售，结果仍可得利润300元，甲种商品的成本是多少元？_____
A: 800 　 B: 700 　 C: 850 　 D: 750
参考答案: D 本题解释:【解析】D。 设甲种商品的成本为x元，则乙种商品的成本为2000－x元，可得：x×（1+50%）×80%+（2000－x）×（1+40%）×80%=2000+300，解得x=750。故选D项。

59、一个班有50名学生，他们的名字都是由2个或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5B: 8C: 10D: 12
参考答案: C 本题解释:【解析】C。不定方程问题。由题意两组学生名字字数相差10，两边人数相同，即其中一组比另一组三名字人数多10人，则2名字人数少10人。

60、甲、乙、丙三名运动员囊括了全部比赛项目的前三名，他们的总分分别是8、7和17分，甲得了一个第一名，已知各个比赛项目分数相同，且第一名的得分不低于二、三名得分的和，那么比赛共有多少个项目?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分，每个项目前三名的分数和至少是3+2+1=6分，所以每个项目前三名的分数和应该是32的大于6的约数，只能是8、16、32;如果是16或32，因为甲得了一个第一，所以甲的得分应大于8，不合题意，所以每个项目前三名的分数和是8分，共有项目32÷8=4个。

61、一批玩具，比进价高200％销售，一段时间后，六一儿童凶促销，玩具按定价6折出售，打折后这批价格比进价高百分之几？_____
A: 20 B: 40 C: 60 D: 80
参考答案: D 本题解释:D。假设进价为100，则打折前售价为100×（1＋200％）＝300，打折后售价为300×60％＝180元，比进价高（180－100）÷100×100％＝80％。故选D项。

62、浓度为20％的盐水若干克，加入100克水后浓度变为15％，若要将盐水的浓度变为10％，需要再加水多少克？_____
A: 120B: 150C: 180D: 200
参考答案: D 本题解释:【答案】D。解析：设盐水原重x克，将盐水的浓度变为10%需再加水y克。根据题意，得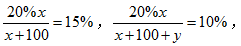解得x=300，y=200。故本题答案选D。

63、将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:A。

64、一艘船从A地行驶到B地需要5天，而该船从B地行驶到A地则需要7天。假设船速、水流速度不变，并具备漂流条件，那么船从A地漂流到B地需要_____天。
A: 40 B: 35 C: 12 D: 2
参考答案: B 本题解释:B。漂流瓶问题。漂流所需时间T=2t逆t顺/（t逆-t顺）（其中t逆和t顺分别表示漂流瓶逆流和顺流所需时间），代入可得：T=2×5×7/（7-5）＝35（天）。

65、为了把2008年北京奥运办成绿色奥运，全国各地都在加强环保，植树造林。某单位计划在通往两个比赛场馆的两条路的(不相交)两旁栽上树，现运回一批树苗，已知一条路的长度是另一条路长度的两倍还多6000米，若每隔4米栽一棵，则少2754棵;若每隔5米栽一棵，则多396棵，则共有树苗_____。
A: 8500棵B: 12500棵C: 12596棵D: 13000棵
参考答案: D 本题解释:答案：D。设两条路共长z米，共有树苗y棵，在两条路的两旁栽树则有4条线要栽树。则x÷4+4=y+2754，x÷5+4=y-396，解出y=13000棵，所以选D。

66、2011×201+201100—201.1×2910的值为_____。
A: 20110B: 21010C: 21100D: 21110
参考答案: A 本题解释:原式=2011×（201+100—291）=2011×10=20110。故选A。

67、地铁检修车沿地铁线路匀速前进，每6分钟有一列地铁从后面追上，每2分钟有一列地铁迎面开来。假设两个方向的发车间隔和列车速度相同，则发车间隔是_____。
A: 2分钟B: 3分钟C: 4分钟D: 5分钟
参考答案: B 本题解释:【答案】B。解析：此题为水速问题的变种，设两列地铁间的距离为1，则二者速度差为1/6，速度和为1/2，由水速问题的公式得，地铁的速度为(1/6+1/2)÷2=1/3，即3分钟发车一次。

68、一只装有动力桨的船，其单独靠人工划船顺流而下的速度是水流速度的3倍，现在该船靠人工划动从a地到顺流到达b地，原路返回时只开足动力桨行驶，用时比来时少 ，问船在静水中开足动力桨行驶的速度是人工划桨的速度的多少倍? _____
A: 2 B: 3 C: 4 D: 5
参考答案: B 本题解释:【答案】B【解析】假设水流速度为“1”，a地到b地的距离为15。则人工划船的顺流速度为3，人工划船的静水速度为3-1=2。人工划船从a地顺流到b地时间为15÷3=5，故动力桨从b地逆流到a地时间为5×（1- ）=3，故动力桨的逆流速度为15÷3=5，动力桨的静水速度为5+1=6。因此，船在静水中开足动力桨行驶的速度是人工划桨的速度的6÷2=3倍。

69、有一笔奖金，按1：2：3的比例来分，已知第三人分450元，那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知，这笔奖金共分为6份，而分到3份的第三人拿到了450元，则6份当是450×2=900元。所以正确答案为C项。

70、某公司要到外地去推销产品，产品成本为每件3000元。从公司到外地距离是400千米，运费为每件产品每运1千米收1.5元。如果在运输及销售过程中产品的损耗是10%，那么公司要想实现25%的利润率，零售价应是每件多少元? _____
A: 4800B: 5000C: 5600D: 6000
参考答案: B 本题解释:【答案】B。解析：以1件商品为例，成本为3000元，运费为1.5×400=600元，则成本为3000+600=3600元，要想实现25%的利润率，应收入3600×（1+25%）=4500元;由于损耗，实际的销售产品数量为1×（1-10%）=90%，所以实际零售价为每件4500÷90%=5000元。

71、甲、乙、丙练习投篮球，一共投了3150，共有64次没投进。已知甲和乙投进348次，乙和丙一共投进369次，乙投进多少个？_____
A: 28 B: 31 C: 30 D: 33
参考答案: B 本题解释:【解析】B。甲＋乙＋丙＝150－64＝86，甲＋乙＝48，乙＋丙＝69，故乙＝（甲＋乙）-（乙＋丙）－（甲＋乙＋丙）＝48＋69－86＝31次。

72、旅客携带了30公斤行李从A地乘飞机去B地，按民航规定，旅客最多可免费携带20公斤行李，超重部分每公斤按飞机票价格的1.5%购买行李票，现该旅客购买了120元的行李票，则他的飞机票价格应是多少？_____
A: 10000 B: 800 C: 600 D: 400
参考答案: B 本题解释:【解析】B。行李超重部分每千克收取120÷（30－20）＝12元，则飞机票价为12÷1.5％＝800元。

73、甲、乙两港相距720千米，轮船往返两港需要35小时，逆流航行比顺流航行多花5个小时;帆船在静水中每小时行驶24千米，问帆船往返两港需要多少小时?_____
A: 58B: 60C: 64D: 66
参考答案: C 本题解释:C。分析可知轮船逆流航行了20小时，顺流航行了15小时。可得水流速度是（720÷15—720÷20）÷2=6千米/小时，所以帆船顺水速度是24+6=30千米/小时，逆水速度是24—6=18千米/小时，往返需要720÷30+720÷18=64小时。

74、某养殖场养了224头牧畜。其中羊比牛多38只,牛比猪多6只。如果将牛总数的75%用来换羊,一头牛换5只羊,那么,羊总共有多少只?_____
A: 342B: 174C: 240D: 268
参考答案: A 本题解释:【答案】A。解析:根据题意,设该养殖场原有羊x只、牛y只、猪z只,由题意得:x-y=38;y-z=6;x+y+z=224,解得x=102,y=64,那么用牛换羊后,羊总共有102+64×75%×5=342只。故选A。

75、19991998的末位数字是：_____
A: 1B: 3C: 7D: 9
参考答案: A 本题解释:A。【解析】此题关键是要考察末位数的变化情况，9的一次幂、二次幂、三次幂、四次幂……的尾数呈9、1、9、1……变化，即其奇数次幂时尾数是9，偶数次幂时尾数是1，所以选A。

76、_____
A: 2cmB: 3cmC: 3.5cmD: 4cm
参考答案: A 本题解释:【答案】A。解析：

77、某服装厂要生产一批某种型号的学生服，已知每3米长的某种面料可做上衣2件。或做裤子3条，计划用300米长的这种布料生产学生服，应用多少米布料产生上衣，才能恰好配套?_____
A: 120B: 150C: 180D: 210
参考答案: C 本题解释:答案：C【解析】3米长可做上衣2件，或裤子3条，则300米布料可做上衣200件，或裤子300条，即如需成套，则上衣和裤子的数量必须同样多，那么上衣所用布料当为3/5，即180米，裤子为120米，共可做120套服装。所以答案为选项C。

78、某市财政局下设若干处室，在局机关中不是宣传处的有206人，不是会计处的有177人，已知宣传处与会计处共有41人，问该市财政局共有多少人？_____
A: 218 B: 247 C: 198 D: 212
参考答案: D 本题解释: 【解析】由题意有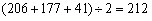：人。所以选D。

79、有一个正方形花池，周围用边长25cm的方砖铺了一条宽1.5米的小路，共用1776块。花池的面积是多少平方米?_____
A: 111 　　B: 289 　　C: 400　 　D: 10404
参考答案: B 本题解释:【答案】B[解析]水池周围的面积是0.25×0.25×1776=111, 设外围正方形边长X，花池小正方形边长Y，则有X2-Y2=111, 20的平方是400，17的平方是289，400-289刚好是111(熟记20以内平方的好处…)，所以花池面积就是289，选B。

80、某医院内科病房有护士15人，每两人一班，轮流值班，每8小时换班一次，某两人同值一班后，到下次这两人再同值班，最长需要几天_____
A: 15B: 35C: 30D: 5
参考答案: B 本题解释:B.【解析】n×（n-1）/2=15×14/2=105，105×8/24=35。故选B。

81、船在流速为每小时1000米左右的河上逆流而上，行至中午12点时，有一乘客的帽子落到了河里。乘客请求船家返回追赶帽子，这时船已经开到离帽子100米远的上游。已知在静水中这只船的船速为每分钟20米。假设不计调头的时间，马上开始追赶帽子，问追回帽子应该是几点几分？_____
A: 12点10分B: 12点15分C: l2点20分D: 12点30分
参考答案: A 本题解释:【解析】A。本题不需要考虑水速。船和帽子的相对速度为每分钟20米，距离相差100米，可得追上帽子需要5分钟；发现帽子到返回追帽子船走了100米，此段路程所花的时间为5分钟，则追回帽子应该是12点10分。

82、某种型号拖拉机，前轮直径为50厘米，后轮直径为150厘米，拖拉机前进时，前轮转了240圈，求后轮转了多少圈？_____
A: 60B: 40C: 30D: 80
参考答案: D 本题解释:【解析】D。圆的周长与其直径成正比。

83、在距离10千米的两城之间架设电线杆，若每隔50米立一个电线杆，则需要有_____个电线杆。
A: 15B: 201C: 100D: 250
参考答案: B 本题解释:B 【解析】所需数量为长度数除以间隔数加1。

84、从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作，若其中甲、乙两名志愿者都不能从事翻译工作，则不同的选派方案共有_____
A: 280种 B: 240种C: 180种D: 96种
参考答案: B 本题解释: 答案【B】由于甲、乙两名志愿者都不能从事翻译工作，所以翻译工作就是“特殊”位置，因此翻译工作从剩下的四名志愿者中任选一人有C(4,1)=4种不同的选法，再从其余的5人中任选3人从事导游、导购、保洁三项不同的工作有A(5,3)种不同的选法，所以不同的选派方案共有 C(4,1)×A(5,3)=240种，所以选B。

85、2007年4月20日，上证综指早盘高开11点，以3460.90点开盘后，随即逐波上扬，至终盘报收于3584.20点，较上一个交易日上涨了_____
A: 3.56% B: 11点 C: 113.70点 D: 134.30点
参考答案: D 本题解释: 【解析】较上一个交易日上涨多少应该以上个交易日收盘点数为准，所以高开的11点依然属于今天上涨的部分，故有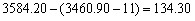点。故选D。

86、2003年7月1日是星期二，那么2005年7月1日是_____。
A: 星期三B: 星期四C: 星期五D: 星期六
参考答案: C 本题解释:【解析】C。2003年7月1日至2005年7月1日相差天数为731天，每星期为7天，731÷7=104还余下3天。所以在周二的基础上加三天，为周五。故选C。

87、田忌与齐威王赛马并最终获胜被传为佳话，假设齐威王以上等马、中等马和下等马的固定程序排阵，那么田忌随机将自己的三匹马排阵时，能够获得两场胜利的概率是_____。
A: 2/3B: 1/3C: 1/6D: 1/9
参考答案: C 本题解释:【答案】C。解析：故正确答案为C。

88、某S为自然数，被10除余数是9，被9除余数是8，被8除余数是7，已知100＜S＜1000，请问这样的数有几个？_____
A: 5 B: 4 　 C: 3 　 D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1，所以这个数字就是几个N的公倍数-1。10，9，8的公倍数为360n（n为自然数），因为100＜S＜1000，所以有两个数符合条件。

89、甲、乙沿同一公路相向而行，甲的速度是乙的1.5倍，已知甲上午8点经过邮局，乙上午10点经过邮局。问：甲乙在中途何时相遇？_____
A: 8点48分 B: 8点30分 C: 9点 D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x，甲就是1.5x，当甲8点到邮局时，乙离邮局还有2个小时的路程（2x），甲乙走完2x路程需要2x/（1.5x+x）=4/5小时=48分钟，加上8点，就是8点48分相遇。

90、小张和小王同时骑摩托车从A地向B地出发，小张的车速是每小时40公里，小王的车速是每小时48公里。小王到达B地后立即向回返，又骑了15分钟后与小张相遇。那么A地与B地之间的距离是多少公里？_____
A: 144B: 136C: 132D: 128
参考答案: C 本题解释:C。相遇的时候小王比小张多走了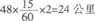，共用时24÷(48-40)=3小时，所以A地与B地之间的距离为48×3-12=132公里。

91、一段路程分为上坡、平路、下坡三段，路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米，路程全长是50千米，小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A 本题解释:A解析：上坡、平路、下坡的速度之比是：14∶25∶36=5∶8∶10平路速度为：3×8/5=24/5(千米/小时)下坡速度为：3×10/5=6(千米/小时)上坡路程为：50×1/(1+2+3)=50/6=25/3(千米)平路路程为：50×2/(1+2+3)=50/3(千米)下坡路程为：50×3/(1+2+3)=25(千米)25/3÷3+50/3÷24/5+25÷6=10(5/12)(小时)故本题选A。

92、一块金与银的合金重250克,放在水中减轻16克。现知金在水中重量减轻1/19，银在水中重量减轻1/10,则这块合金中金、银各占的克数为_____。
A: 100克,150克B: 150克,100克C: 170克,80克D: 190克,60克
参考答案: D 本题解释:【答案】D。解析:设金的质量为x克,银的质量为y克,列方程:x+y=250,x÷l9+y÷10=16,解得x=190,y=60。

93、妈妈给了红红一些钱去买贺年卡，有甲、乙、丙三种贺年卡，甲种卡每张0.50元，丙种卡每张1.20元。用这些钱买甲种卡要比买乙种卡多买8张，买乙种卡要比买丙种卡多买6张。妈妈给了红红多少钱?_____
A: 8元B: 10元C: 12元D: 15元
参考答案: C 本题解释:C解析：盈亏总额为0.5×8+1.2×6=11.2(元)，单价相差1.2-0.5=0.7(元)，所以共可买乙种卡11.2÷0.7=16(张)。妈妈给了红红0.5×(16+8)=12(元)。故本题正确答案为C。

94、在平面直角坐标系中，如果点P(3a-9，1-a)在第三象限内，且横坐标、纵坐标都是整数，则点P的坐标是_____。
A: (一1.一3)B: (一3，一1)C: (一3，2)D: (一2，一3)
参考答案: B 本题解释:B【解析】第三象限内的值都是负值，因此可得。且P点横纵坐标都是整数，因此2，所以P点坐标是（一3，一1）。

95、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 3/2C: 1/3D: 2
参考答案: C 本题解释: C解析：汽车行驶100千米需100÷80=5/4（小时），所以摩托车行驶了5/4+1+1/6=29/12（小时）。如果摩托车一直以40千米/小时的速度行驶，29/12小时可行驶96（2/3）千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C.

96、某剧院有25排座位，后一排比前一排多2个座位，最后一排有70个座位。这个剧院一共有多少个座位?_____
A: 1104　B: 1150　C: 1170　D: 1280
参考答案: B 本题解释:B[解析]最后一排有70个坐位，则前面24排每一排少两个，第一排有70-24×2=22，构成一个等差数列，公差为2，首项为22，S25=25×22+(25×24×2)÷2=1150个，选择B。

97、一间长250米、宽10米、高4米的仓库放置了1000个棱长为1米的正方体箱子，剩余的空间是多少立方米?_____ B: 1500C: 5000D: 9000
参考答案: D 本题解释:D。【解析】进行简单的数字计算即可，250×10×4-1000×1=9000(m3)。

98、小王的爷爷比奶奶大2岁，爸爸比妈妈大2岁，全家五口人共200岁。已知爷爷年龄是小王的5倍，爸爸年龄在4年前是小王的4倍，则小王的爸爸今年多少岁? _____
A: 40B: 36C: 32D: 44
参考答案: B 本题解释:B。假设奶奶和爷爷一样大，妈妈和爸爸一样大，全家年龄和是200+4=204岁，这样爷爷、奶奶的年龄和是10个小王的年龄。而爸爸的年龄是4年前小王的4倍多4岁，换句话说，就是比现在小王年龄的4倍少4×4-4=12岁，妈妈也比现在小王的年龄的4倍少12岁，这样现在全家人的年龄和204+12+12=228岁，则小王的年龄为228÷（5×2+4×2+1）=12岁，爸爸的年龄为（12-4）×4+4=36岁。

99、有一1500米的环形跑道,甲乙两人同时同地出发,若同方向跑50分钟后,甲比乙多绕整一圈;若以相反方向跑2分钟后二人相遇。则乙的速度为_____。
A: 330米/分钟B: 360米/分钟C: 375米/分钟D: 390米/分钟
参考答案: B 本题解释:【答案】B。解析:同向跑时,50分钟后甲与乙第一次相遇,则甲与乙的速度差为1500÷50=30米/分钟;反向跑时,2分钟后甲乙二人第一次相遇,则甲与乙的速度和为1500÷2=750米/分钟,故乙的速度为（750-30）÷2=360米/分钟。

100、3点19分时，时钟上的时针与分针所构成的税角为几度？_____
A: 14度B: 14.5度C: 15度D: 15.5度
参考答案: B 本题解释:【解析】B。14. 5度。一圈是360度。分针跑60分钟是一圈，360/60=每分钟6度 时针跑12小时是一圈，360/（12*60）=0.5度每分钟 3点19分时候分针跑了6*19=114。时针0.5*199=99.5。