微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、果园里有梨树、桃树、核桃树共526棵,梨树比桃树的2倍多24棵,核桃树比桃树少18棵。求桃树有多少棵?_____
A: 105B: 115C: 125D: 130
参考答案: D 本题解释:参考答案 题目详解:解法一:设桃树有
题目详解:解法一:设桃树有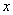 棵,那么梨树有
棵,那么梨树有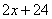 棵,核桃树有
棵,核桃树有 棵,因此
棵,因此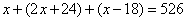 解得,
解得,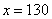 。所以,选D。解法二:“梨树比桃树的2倍多24棵”,如果梨树少24棵,则刚好是桃树的2倍。“核桃树比桃树少18棵”,如果核桃树多18棵,那么刚好与桃树相同。则有:桃树的数目是:
。所以,选D。解法二:“梨树比桃树的2倍多24棵”,如果梨树少24棵,则刚好是桃树的2倍。“核桃树比桃树少18棵”,如果核桃树多18棵,那么刚好与桃树相同。则有:桃树的数目是: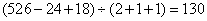 (棵)梨树的数目是:
(棵)梨树的数目是: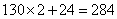 (棵)核桃树的数目是:
(棵)核桃树的数目是: (棵)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
(棵)考查点:数量关系>数学运算>和差倍比问题>和差倍问题
2、某商店,雨天每天售出雨伞30把,晴天每天售出雨伞12把,连续数天平均每天售出16把雨伞,共售出144把,晴天有_____天。
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:售出雨伞的总天数为:144÷16=9天,假设全是雨天售出的,则雨伞数应该为:30×9=270,这比实际多算了270-144=126。这些是把晴天售出的伞都算成雨天的了,雨天比晴天每天多售出的雨伞数为:30-12=18,那么晴天有: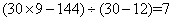 天。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
天。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
3、某区要从10位候选人中投票选举人大代表,现规定每位选举人必须从这10位中任选两位投票,问至少要有多少位选举人参加投票,才能保证有不少于10位选举人投了相同两位候选人的票?_____
A: 382位B: 406位C: 451位D: 516位
参考答案: B 本题解释:【答案】B。解析:从10位候选人中选2人共有种票,则每种票有9张相同时需要×9=405个人投票,那么只需要再加一人可以保证有不少于10人投了相同两位候选人的票。
4、甲、乙、丙三队在A、B两块地植树,A地要植树900棵,B地要植树1250棵,已知甲、乙、丙每天分别能植树24,30,32棵,甲在A地植树,丙在B地植树,乙先在A地植树,然后转到B地植树。两块地同时开始同时结束,乙应在开始后第几天从A地转到B地?_____
A: 5B: 7C: 9D: 11
参考答案: D 本题解释:D【解析】 植树共需(900+1250)÷(24+30+32)=25(天)。乙应在A地干(900-24×25)÷30=10(天),第11天转到B地。故本题正确答案为D。
5、 (2009吉林)A、B两座城市距离:300千米,甲乙两人分别从A、B两座城市同一时间出发,已知甲和乙的速度都是50km/h,苍蝇的速度是100km/h,苍蝇和甲一起出发,然后遇到乙再飞回来,遇到甲再回去,直到甲乙相遇才停下来,请问苍蝇飞的距离是_____km?
A: 100B: 200C: 300D: 400
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:甲乙相遇的时间为: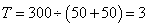 (小时),苍蝇飞行距离
(小时),苍蝇飞行距离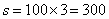 (千米)。所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
(千米)。所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
6、有3个企业共订阅300份《经济周刊》杂志,每个企业至少订99份,最多订101份,问一共有多少种不同的订法? _____
A: 6B: 7C: 8D: 9
参考答案: B 本题解释:B。【解析】份数的选择有99,100,101或100,100,100,则第一种选择有A33=6种订法,6+1=7
7、一篇文章,现有甲、乙、丙三人,如果由甲、乙两人合作翻译,需要10小时完成,如果由乙、丙两人合作翻译,需要12小时完成。现在先由甲、丙两人合作翻译4小时,剩下的再由乙单独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,要多少个小时完成?_____
A: 15B: 18C: 20D: 25
参考答案: A 本题解释:正确答案是A考点工程问题解析设总量为1,由题意知甲乙合作的效率为1/10,乙丙合作的效率为1/12。题目给出完成该项工程的过程是甲丙先合作4个小时,乙单独翻译12个小时。在这个工作过程中,甲完成了4个小时的工作量,已完成了12个小时的工作量,丙完成了4个小时的工作量,保持此总量不变,将乙的工作拆分为三个独立的4个小时,重新为如下工作过程:甲乙先合作4个小时,乙丙再合作4个小时,最后乙单独做4个小时,仍然可以保证工程完成。于是假设乙的效率为y,可知4×1/10+4×1/12+4y=1,解得y=1/15,于是乙单独完成需要15个小时,故正确答案为A。
8、三位采购员定期去某市场采购,小王每隔9天去一次,大刘每隔6天去一次,老杨每隔7天去一次,三人星期二第一次在这里碰面,下次相会将在星期几?_____
A: 星期一 B: 星期五 C: 星期二 D: 星期四
参考答案: C 本题解释: 【解析】C。取9,6,7的最小公倍数得126,即过126天,此三人才能再次相遇,而126天恰好是18个星期,因此下次他们见面还是在星期二。
9、某人登山,上山时每走30分钟,休息10分钟;下山时每走30分钟,休息5分钟;下山的速度是上山速度的1.5倍。如果下山用了2小时15分,那么上山用的时间是_____。
A: 3小时40分B: 3小时50分C: 4小时D: 4小时10分
参考答案: B 本题解释:【答案】B。解析:设上山速度是1,下山的速度是1.5,下山的时间是135分钟,那么走了4个30分钟,休息了3个5分钟,也就是走了2小时,那么路程就是1.5×2=3,上山时速度是1,时间就是3÷1=3小时,也就是走了6个30分钟,这需要休息5个10分钟,总共就用了3小时50分钟。
10、同时扔出A、B两颗骰子(其六个面上的数字都为1,2,3,4,5,6),问两个骰子出现的数字的积为偶数的情形有几种_____。
A: 24千米B: 25千米C: 28千米D: 30千米
参考答案: A 本题解释:正确答案是B考点行程问题解析甲从A地到B地需要100÷10=10小时,为了使乙不比甲晚到B地,乙至多用时10-6=4小时,则乙的速度至少为100÷4=25千米/小时。故正确答案为B。
11、超市规定每3个空汽水瓶可以换一瓶汽水,小李有11个空汽水瓶,最多可以换几瓶汽水_____。
A: 5B: 4C: 3D: 2
参考答案: A 本题解释:正确答案是A考点计数模型问题解析3个空瓶换1瓶水,因此3空瓶=1汽水+1空瓶,可以得出等价公式:2空瓶=1汽水,因此小李的11个空汽水瓶可以换5瓶汽水。故正确答案为A。
12、10个连续偶数的和是以1开始的10个连续奇数和的2.5倍,其中最大的偶数是多少?
A: 34B: 38C: 40D: 42
参考答案: A 本题解释:【答案】A。解析:猜证结合,以1开始的10个连续奇数的和是250,代入答案中得A。
13、一个五位数,左边三位数是右边两位数的5倍,如果把右边的两位数移到前面,则所得新的五位数要比原来的五位数的2倍还多75,则原来的五位数是_____。
A: 12525B: 13527C: 17535D: 22545
参考答案: A 本题解释:【答案解析】直接代入,选A。
14、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车慢4/5,则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:答案:D【解析】设某人速度为v,则小偷速为0.5v,汽车速为5v,10秒钟内,与小偷相差(0.5+5)v×10=55v,追求时速差为0.5v,所以所需时间为110秒。
15、某单位安排职工参加百分制业务知识考试,小周考了88分,还有别外2人的得分比他低。若所有人的得分都是整数,没有人得满分,且任意5人的得分不完全相同,问参加考试的最多有多少人?_____
A: 38B: 44C: 50D: 62
参考答案: C 本题解释:正确答案是C,全站数据:本题共被作答1次,正确率为0.00%,易错项为B解析为了让参加考试的人”最多”,则尽可能在每一个分数段都有尽可能多的人分数相同。从88分-99分,共有12个整数分数可以重复,同时又由于”任意5人的得分不完全相同”,所以要求重复的分数的人数最多为4人。这样一共有48人,再加上两个低于88分的人,所以最多50人。故正确答案为C。速解本题与”抽屉原理”的反客为主思想完全相同,逆向思维简化思维量。考点抽屉原理问题
16、某地区水电站规定,如果每月用电不超过24度,则每度收9分钱;如果超过24度,则多出度数按每度2角收费,若某月甲比乙多交了9.6角,则甲交了几角几分?_____
A: 27角6分B: 26角4分C: 25角5分D: 26角6分
参考答案: A 本题解释:【解析】A。如果每月用电24度,则应该交24×9=216分钱,即21.6角。答案中没有这个答案,就是说甲已经超过了这个规定数字。设他用了24+M度电,则交了24×9+M×20=216+20×M,甲比乙多交了96分,则216+20×M-96可以被9整除,即(20×M+120)÷9。M=3时,(20×M+120)÷9=2,即甲用了27度电,用了276分。
17、某人要上某大厦的10楼,他从1楼到5楼用了100秒,按此速度,他到10楼还需要的时间为_____秒。
A: 225B: 125C: 100D: 150
参考答案: B 本题解释:参考答案:B题目详解:从1楼到5楼共有5-1=4段楼梯,每层楼梯花了100÷4=25秒。从5楼到10楼共有10-5=5段楼梯,从5楼道10楼需要时间为:25×5=125秒。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树
18、甲从A地到B地需要30分钟,乙从B地到A地需要45分钟,甲乙两人同时从A、B两地相向而行,中间甲休息了20分钟,乙也休息了一段时间,最后两人在出发40分钟后相遇。问乙休息了多长时间?_____
A: 25B: 20C: 15D: 10
参考答案: A 本题解释:正确答案是A考点行程问题解析甲和乙走完全程分别要30、45分钟。甲在相遇时走了20分钟,走了全程的2/3,乙走了全程的1/3,应该用45×1/3=15分钟。因此乙休息了40-15=25分钟。因此正确答案为A。
19、一列队伍沿直线匀速前进,某时刻一传令兵从队尾出发,匀速向队首前进传送命令,他到达队首后马上原速返回,当他返回队尾时,队伍行进的距离正好与整列队伍的长度相等。问传令兵从出发到最后到达队尾所行走的整个路程是队伍长度的多少倍?_____
A: 0.5 B: 1.5C: 1 D: 2
参考答案: C 本题解释:【答案】C。解析:从队尾到队首,这是一个追及过程,追及的路程等于队伍的长。从队首返回队尾,这是一个相遇过程,返回队尾所行的路程都等于队伍的长。
20、河流赛道长120米,水流速度2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48B: 50C: 52D: 54
参考答案: C 本题解释:正确答案是C考点行程问题解析由于水速为2米/秒,所以顺行时候甲船速度是8米/秒,乙船速度是6米/秒。逆行时候甲船速度是4米/秒,乙船速度是2米/秒。甲乙的两次相遇分别在甲船第一次返回和甲船第二次顺行途中,甲第一次返回原地花费时间为120/8+120/4=45秒,此时乙到达对岸,逆水往回走,两船距离120-(4-2)×(45-120/6)=70米,再次相遇需要的时间为70÷(8+2)=7。所以总时间为45+7=52秒。故正确答案为C。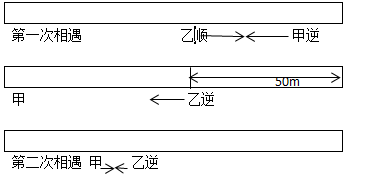
21、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+(-7)=-12。故本题选C。
22、1005×10061006-1006×10051005=? _____
A: 0 B: 100 C: 1000 D: 10000
参考答案: A 本题解释:【答案】A。解析:1005×10061006-1006×10051005=1006×1006×10001-1006×1005×10001=0。即正确答案为A。
23、(111+222+333+444)×55×666=_____
A: 41789201B: 40659308C: 40659300D: 41789205
参考答案: C 本题解释:正确答案是C考点计算问题解析原式=111×(1+2+3+4)×55×666=111×10×55×666,易知该式计算值末位数为0,仅C项符合。故正确答案为C。标签尾数法
24、某住户安装了分时电表,白天电费是0.55元,夜晚是0.3元,计划7月用电400度,电费不能超过160元,问白天最多不能超过多少度?_____
A: 150B: 160C: 170D: 180
参考答案: B 本题解释:正确答案是B考点鸡兔同笼问题解析解析1:设7月份白天用电x度,则夜晚用电(400-x)度,根据题意得,0.55x+0.3(400-x)≤160,即求满足不等式的x的最大值,经分析可知当不等式右边取160时,x取最大值,即此时0.55x+0.3(400-x)=160,解得x=160,故正确答案为B。解析2:本题也可采用十字交叉法。假设400度全部白天用,总电费:400×0.55=220;400度全部晚上用,总电费:400×0.3=120,而实际电费为160,则进行十字交叉计算,由题意可知白天用电量与晚上用电量之比为(160-120):(220-160)=2:3,因此白天用电量为400×2/5=160,故正确答案为B。秒杀技先看成用电400度全是按夜间电价,则电费为120元,距离160元的电费还差40元,这40元将全部用来支付白天用电需要多支付的部分。而白天电价比夜间电价高0.25元,因此这40元只允许白天用电:40÷0.25=160度,故正确答案为B。
25、松鼠妈妈采松果,晴天每天可采20个,雨天每天只能采12个。它一连几天共采了112个松果,平均每天采14个。这几天中有几天下雨?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:【答案解析】松鼠妈妈一连采了松果的天数为:112÷14=8(天)。设雨天有x天,则晴天有(8-x)天,列方程得20×(8-x)+12x=1125×(8-x)+3x=28x=6故本题正确答案为D。
26、哥哥的年龄和妹妹现在的年龄一样时,妹妹是9岁。妹妹的年龄和哥哥现在的年龄一样时,哥哥是24岁。问妹妹现在的年龄是多少岁?_____
A: 14B: 15C: 17D: 20
参考答案: A 本题解释:答案:A【解析】由题意可得妹妹与哥哥岁数差为(24-9)÷3=5(岁),故妹妹现在的年龄为5+9=14(岁)。
27、小王和小李6小时共打印了900页文件,小王比小李快50%。请问小王每小时打印多少页文件?_____
A: 60B: 70C: 80D: 90
参考答案: D 本题解释: 【解析】D。设小王每小时打印X页,因为小王比小李快50%,则小李每小时打印为X (1-50%)页,则根据题意可列:6X (1-50%)+6X=900,则X=90。
28、一口水井,在不渗水的情况下,甲抽水机用4小时可将水抽完,乙抽水机用6小时可将水抽完。现用甲、乙两台抽水机同时抽水,但由于渗水,结果用了3小时才将水抽完。问在渗水的情况下,用乙抽水机单独抽,需几小时抽完?_____
A: 12小时B: 13小时C: 14小时D: 15小时
参考答案: A 本题解释:正确答案是A考点工程问题解析
29、将 九个自然数分成三组,每组三个数,第一组三个数之积是48。第二组三个数之积是45,三组数字中数字之和最大是多少?_____
九个自然数分成三组,每组三个数,第一组三个数之积是48。第二组三个数之积是45,三组数字中数字之和最大是多少?_____
A: 15B: 17C: 18D: 20
参考答案: C 本题解释:参考答案:C题目详解:第二组三个数的积是 :45只能是
:45只能是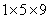 或
或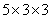 ,但不可能出现2个3,所以第二组只能是5、9、1;第一组三个数的积是
,但不可能出现2个3,所以第二组只能是5、9、1;第一组三个数的积是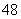 :在剩下的2、3、4、6、7、8中,第一组只能是
:在剩下的2、3、4、6、7、8中,第一组只能是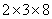 或
或 。(1)若第一组是
。(1)若第一组是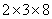 ,则第三组只能是4、6、7,此时,三组数字的数字之和分别为:
,则第三组只能是4、6、7,此时,三组数字的数字之和分别为: ,
, ,
,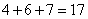 ;(2)若第一组是
;(2)若第一组是 ,则第三组只能是3、8、7,此时,三组数字的数字之和分别为:
,则第三组只能是3、8、7,此时,三组数字的数字之和分别为: ,
,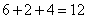 ,
,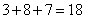 ;所以三组数字中三个数之和最大是18。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
;所以三组数字中三个数之和最大是18。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
30、如图:甲,乙二人分别从A,B两地同时相向出发,往返于A、B之间,第一次相遇在距A地30公里处,第二次相遇地点在距第一次相遇地右边10公里处:问A、B两点相距多远?_____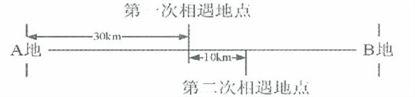
A: 90B: 75C: 65D: 50
参考答案: C 本题解释:参考答案:C题目详解:解法一:两人第一次相遇,共同走完了一个全程,第二次相遇共同走完了3个全程。第一次相遇甲走了30千米,那么第2次相遇时,甲共走了3×30=90千米,实际上甲还差30+10=40千米才走完两个全程。AB两地的距离是:(90+40)÷2=65公里。解法二:“单岸型”,两次相遇问题: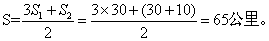 所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
31、有三块草地,面积分别是4亩、8亩、10亩。草地上的草一样厚,而且长得一样快,第一块草地可供24头牛吃6周,第二块草地可供36头牛吃12周。问第三块草地可供50头牛吃几周?_____
A: 6B: 9C: 3D: 7
参考答案: B 本题解释:参考答案:B题目详解:根据题意:此题属于M头牛吃W亩草问题,将单位牧场的牛数代入“N”;单位牧场草的原有存量为y;单位时间草的增长量即自然增长速度为x;第三块地可供50头牛存量完全消失所消耗用的时间3为T;代入公式: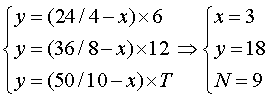 所以,选B考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>M头牛吃W亩草问题
所以,选B考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>M头牛吃W亩草问题
32、现有21朵鲜花分给5人,若每个人分得的鲜花数各不相同,则分得鲜花最多的人至少分得_____朵鲜花。
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:正确答案是A考点多位数问题解析要使分得最多花的人分到的花尽可能的少,那么其他人分到的花尽可能的多。5人分到的花应尽量接近,以保证分得最多花的人分到的花尽可能少,所以最好是5个连续的自然数,21÷5=4.2,所以5人先分花数为2、3、4、5、6。2+3+4+5+6=20,还剩1朵花未分出。剩下的1朵花只能分给之前分到6朵花的人。则分得最多的人至少分得7朵鲜花,正确答案为A。
33、取甲种硫酸300克和乙种硫酸250克,再加水200克,可混合成浓度为50%的硫酸;而取甲种硫酸200克和乙种硫酸150克,再加上纯硫酸200克,可混合成浓度为80%的硫酸。那么,甲、乙两种硫酸的浓度各是多少?_____
A: 75%,60%B: 68%,63%C: 71%,73%D: 59%,65%
参考答案: A 本题解释:【答案】A。解析:
34、有一部96集的电视纪录片从星期三开始在电视台播出。正常情况下,星期二到星期五每天播出1集,星期六、星期天每天播出两集,星期一停播。播完35集后,由于电视台要连续3天播出专题报道,该纪录片暂时停播,待专题报道结束后继续按常规播放。那么该纪录片最后一集将在_____播出。
A: 星期二B: 星期五C: 星期六D: 星期日
参考答案: C 本题解释:正确答案是C考点周期问题解析周三开播,每周播4+2×2=8集,每个周期在周二结束;正常播完需要96÷8=12周整,所以正常播完是在周二;播完35集,35÷8=4……3,则此时为周五,故专题报道播出时间为周六、周日、周一,正常情况下,纪录片应播出4集,故原本周二结束播放的纪录片,还剩下4集,则可知最后一集在周六播出。故正确答案为C。
35、一篇文章,现有甲乙丙三人,如果由甲乙两人合作翻译,需要10小时完成,如果由乙丙两人合作翻译,需要12小时完成,现在先由甲丙两人合作翻译4小时,剩下的再由乙单 独去翻译,需要12小时才能完成,则,这篇文章如果全部由乙单独翻译,需要_____小时能够完成。
A: 15B: 18C: 20D: 25
参考答案: A 本题解释:正确答案是 A。考点:工程问题解析:设总量为1,由题意知甲乙合作的效率为1/10,乙丙合作的效率为1/12。题目给出完成该项工程的过程是甲丙先合作4个小时,乙单独翻译12个小时。在这个工作过程中,甲完成了4个小时的工作量,已完成了12个小时的工作量,丙完成了4个小时的工作量,保持此总量不变,将乙的工作拆分为三个独立的4个小时,重新为如下工作过程:甲乙先合作4个小时,乙丙再合作4个小时,最后乙单独做4个小时,仍然可以保证工程完成。于是假设乙的效率为y,可知4×1/10+4×1/12+4y=1,解得y=1/15,于是乙单独完成需要15个小时,故正确答案为A。
36、某人工作一年的报酬是8400元和一台电冰箱,他干了7个月不干了,得到3900元和一台电冰箱。这台电冰箱价值多少元?_____
A: 400B: 2000C: 2400D: 3500
参考答案: C 本题解释:C【解析】设此台冰箱价值x元,则有(8400+x)÷12=(3900+x)÷7,解得x=2400。
37、某班男生比女生人数多80%,一次考试后,全班平均成级为75分,而女生的平均分比男生的平均分高20%,则此班女生的平均分是_____。
A: 84分B: 85分C: 86分D: 87分
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析解析1:设男生的平均分为x,则女生的平均分是1.2x。由题意得男、女人数之比为1.8:1,由十字交叉法得(1.2x-75):(75-x)=1.8:1,解得x=70分。则女生的平均分为1.2×70=84分,故正确答案为A。解析2:设男生的平均分为z,女生人数为y。则女生的平均分是1.2z,男生的人数是1.8y。由题意得:1.8zy+1.2zy=75×2.8y,解得z=70分。因此女生的平均分是1.2×70=84分,故正确答案为A。秒杀技由“女生的平均分比男生的平均分高20%”知女生的平均分一定能被12整除,只有A选项符合条件,故正确答案为A。
38、(2009-北京社会)甲、乙、丙三个滑冰运动员在一起练习滑冰,已知甲滑一圈的时间,乙、丙分别可以滑一又四分之一圈和一又六分之一圈,若甲、乙、丙同时从起点出发,则甲滑多少圈后三人再次在起点相遇?_____
A: 8B: 10C: 12D: 14
参考答案: C 本题解释:参考答案:C题目详解:根据题意,“三人再次在起点相遇”,则三人滑的圈数必须都为整数;相同时间内,甲、乙、丙滑的圈数之比为: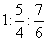 ,将其转化为整数比;将他们同时乘以4,6的最小公倍数12,即为12:15:14;则三人分别滑12、15、14圈时再次在起点相遇;因此,选C。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>三个数的最大公约数和最小公倍数
,将其转化为整数比;将他们同时乘以4,6的最小公倍数12,即为12:15:14;则三人分别滑12、15、14圈时再次在起点相遇;因此,选C。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>三个数的最大公约数和最小公倍数
39、(2009.黑龙江)小强前三次的数学测验平均分是88分,要想平均分达到90分以上,他第四次测验至少要得多少分?_____
A: 98分B: 92分C: 94分D: 96分
参考答案: D 本题解释:参考答案 题目详解:前3次测验的总分为:88×3=264分;要使前4次测验的平均分≥90分;即前4次测验的总得分≥90×4=360分;前4次测验的总得分=前3次测验的总分+第四次测验得分,故第四次测得分=前4次测验的总得分-前3次测验的总分;第四次测得分≥360-264=96分。即最少要得96分;所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
题目详解:前3次测验的总分为:88×3=264分;要使前4次测验的平均分≥90分;即前4次测验的总得分≥90×4=360分;前4次测验的总得分=前3次测验的总分+第四次测验得分,故第四次测得分=前4次测验的总得分-前3次测验的总分;第四次测得分≥360-264=96分。即最少要得96分;所以,选D。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>算术平均值
40、已知a-b=46,a÷b÷c=2,a÷b-c=12,问a+b的值是_____。
A: 50B: 60C: 70D: 80
参考答案: A 本题解释:正确答案是A考点计算问题解析由a÷b÷c=2,a÷b-c=12,将a÷b看成一个整体,据此可求得:a÷b=24,c=12。又知a-b=46,联立可求得:a=48,b=2,因此a+b=50,故选择A选项。
41、小明和小方各走一段路,小明走的路程比小方多1/5,小方用的时间比小明多1/8。小明和小方的速度之比是多少?_____
A: 37∶14B: 27∶20C: 24∶9D: 21∶4
参考答案: B 本题解释: B【解析】依题意,小明与小芳路程的比是(1+1/5):1=6:5小明与小芳时间的比是1:(1+1/8)=8:9小明与小芳速度的比是:6/8:5/9=27:20。
42、小王从家开车上班,其实行驶10分钟后发生了故障,小王从后备箱中取出自行车继续赶路,由于自行车的车速只有汽车的3/5,小王比预计时间晚了20分钟到达单位,如果之前汽车再多行驶6公里,他就能少迟到10分钟,从小王家到单位的距离是_____公里。
A: 12B: 14C: 15D: 16
参考答案: D 本题解释:正确答案是D考点行程问题解析由题意可知,汽车和自行车的速度之比为5:3,因此相同路程下汽车和自行车的用时之比为3:5。迟到20分钟,则余下的路程汽车30分钟,自行车50分钟,所以总路程开车需40分钟;迟到10分钟,则余下的路程汽车15分钟,自行车25分钟,后面一种情况比前面一种汽车多开了15分钟,行驶了6公里,因此全程的距离为6÷15×40=16公里,故正确答案为D。标签比例转化
43、一个人从某服装店花60元买走一件衣服,付了100元,售货员因为没有零钱,去隔壁商店换出零钱给顾客。后来发现那100元是假钞,该服装店只好赔给隔壁商店100元,若卖出的服装进价为40元,则该服装店共赔了多少元?_____
A: 40B: 80C: 100D: 180
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析衣服值40元,找给买家40元,总共赔了40+40=80元。赔隔壁商店的100元,与此前从隔壁商店换取的100元相抵消,故而不是损失。故正确答案为B。
44、(2006江西)运送一批货物总运费为4200元,A、B两家运输公司同时运送8小时完成,A公司单独运输需14小时完成。现由A公司单独运送若干小时后,再由B公司单独运送剩下的货物。这样共用18小时全部运完。那么A、B两公司应分别获得:_____
A: 2100元,2100元B: 600元,3600元C: 1400元,2800元D: 800元,3400元
参考答案: B 本题解释:参考答案:B题目详解:解法一根据题意,设A、B两家运输公司的工作效率分别为x,y第一种运送方式的工作总量为:工作总量=工作效率×工作时间=8(x+y);第二种运送方式的工作总量为:工作总量=工作效率×工作时间=14x;由一二两种运送方式,得出8(x+y)=14x,解得x:y=4:3;第三种运送方式工作总量为:设现甲单独运送了t小时,则乙继续运送时间为(18-t),工作总量=甲的工作总量+乙的工作总量=甲的工作效率×甲的工作时间+乙的工作效率×乙的工作时间=xt+y(18-t),因为工作总量是一定的,所以xt+y(18-t)=14x,解得t=2;得出运输费用为:工作效率×工作时间×总费用,所以A运输公司所得费用:4200×1/14×2=600元;B公司的费用:4200-600=3600;因此,选B。解法二根据题意,设总工作量为"1”A公司的工作效率:工作效率=工作总量÷工作时间=1÷14=1/14;A、B公司的工作效率之和:工作效率=工作总量÷工作时间=1÷8=1/8;故B公司工作效率为:A、B公司工作效率之和-A工作效率=1/8-1/14=3/56;设A运送了t小时,则第三种运送方式的工作总量为:工作总量=工作效率×工作时间=1/14t+3/56(18-t)=1;解得t=2。得出运输费用为:工作效率×工作时间×总费用,所以A运输公司所得费用:4200×1/14×2=600元;B公司的费用:4200-600=3600;因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
45、某公司100名员工对甲、乙两名经理进行满意度评议,对甲满意的人数占全体参加评议的3/5,对乙满意的人数比甲的人数多6人,对甲乙都不满意的占满意人数的1/3多2人,则对甲乙都满意的人数是_____。
A: 36B: 26C: 48D: 42
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析对甲满意的人数为60人,对乙满意的人数为66人,设对甲、乙都满意的人数为X,则对甲、乙都不满意的人数为1/3X+2,由两集合容斥原理的推论公式可知,100-(1/3X+2)=60+66-X,解得X=42,故正确答案为D。两集合容斥原理推论公式:满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。
46、某校图书馆新购进120本图书,其中教育学类书60本,心理学类40本,有30本既不属于教育学类也不属于心理学类,则这批书中教育心理学书有多少本?_____
A: 10B: 20C: 30D: 40
参考答案: A 本题解释:A【解析】设教育心理学书购进X本。则根据两集合容斥原理核心公式可得︰60+40-x=120-30x=10,故答案为A选项。
47、单独完成某项工作,甲需要16小时,乙需要12小时,如果按照甲、乙、甲、乙……的顺序轮流工作,每次1小时,那么完成这项工作需要多长时间?_____
A: 13小时40分钟B: 13小时45分钟C: 13小时50分钟D: 14小时
参考答案: B 本题解释:答案:B.[解析]本题为工程类题目。设总工程量为48,则甲的效率是3,乙的效率是4,工作12小时后,完成了42。第12小时甲做了3,完成了总工程量45,剩余的3由乙在第十四小时完成。在第十四小时里,乙所用的时间是3/4小时,所以总时间是13.75小时。
48、张先生向商店订购某种商品80件,每件定价100元。张先生向商店经理说:“如果你肯减价,每减1元,我就多订购4件。”商店经理算了一下,如果减价5%,由于张先生多订购,仍可获得与原来一样多的利润。则这种商品每件的成本是_____。
A: 75元B: 80元C: 85元D: 90元
参考答案: A 本题解释:【解析】A。设成本为x元。减价5%即减去了5元,同样就要多购买4×5=20件,利润相同,即可得到等式(100-x)×80=(95-x)×(80+20),得x=75。
49、某城市居民用水价格为:每户每月不超过5吨的部分按4元/吨收取,超过5吨不超过10吨的部分按6元/吨收取,超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元,则该户居民这两个月用水总量最多为多少吨?_____
A: 21B: 24C: 17.25D: 21.33
参考答案: A 本题解释:【解析】A。水量越大,费用越高,所以要用水最多,所以每个月应该用满10吨,所以总吨数为20+(108-100)/8=21.
50、某公司中午订餐,周一有27人订餐,周二有39人订餐,周三有43人订餐,周四有41人订餐,周五有39人订餐。如果在这五天至少有一天订餐的人有39人,那么五天都订餐的最多有多少人?_____
A: 27B: 26C: 25D: 24
参考答案: A 本题解释:参考答案:A题目详解:依题意:将39人分为仅订餐一次和五天都订餐的;那么五天都订餐的最多有: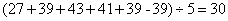 人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
人;而周一只有27人订餐;因此最多只有27人五天都订餐。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>最值问题
51、 _____
_____
A: 3B: 4C: 5D: 6
参考答案: C 本题解释:正确答案是C考点计算问题解析
52、有一食品店某天购进了6箱食品,分别装着饼干和面包,重量分别为8、9、16、20、22、27千克。该店当天只卖出1箱面包,在剩下的5箱中饼干的重量是面包的两倍,则当天食品店购进了_____千克面包。
A: 44B: 45C: 50D: 52
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由剩下的饼干重量是面包的两倍可知,剩下5箱的总重量一定能被3整除;6箱的总重量是8+9+16+20+22+27=102千克,也能被3整除,因此卖掉的一箱面包的重量也能被3整除,只能是9千克或27千克。若卖掉的一箱面包的重量是9千克,则剩下的面包重(102-9)÷3=31千克,剩余的各箱重量无法组合得到31。所以卖出的面包重27千克,剩余面包重(102-27)÷3=25千克。因此共购进了27+25=52千克面包,故正确答案为D。
53、小张到文具店采购办公用品,买了红黑两种笔共66支。红笔定价为5元,黑笔的定价为9元,由于买的数量较多,商店给与优惠,红笔打八五折,黑笔打八折,最后支付的金额比核定价少18%,那么他买了红笔_____。
A: 36支B: 34支C: 32支D: 30支
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析解析1:设买红笔A支,黑笔B支,由题意得:A+B=66······(1)(5A+9B)×0.82=5A×0.85+9B×0.8······(2)由(2)式得B=5/6A,则A=66×[6/(6+5)]=36。解析2:红笔打八五折,黑笔打八折,总价打八二折,相当于红笔和黑笔都打八二折,设红笔A支,黑笔B支,则(0.85-0.82)×5A=(0.82-0.80)×9B,得B=5/6A,则A=66×[6/(6+5)]=36。故正确答案为A。
54、甲购买了A、B、C三种书籍各若干本捐赠给希望小学。其中B书籍比C书籍少了3本,比A书籍多2本;B书籍的单价比A书籍低4元,比C书籍高4元。其购买B书籍的总开销与C书籍相当,比A书籍少4元。问甲购买三种书籍一共用了多少元?_____
A: 724B: 772C: 940D: 1084
参考答案: D 本题解释:正确答案是D,全站数据:本题共被作答1次,正确率为0.00%,易错项为B解析直接列方程求解:设B类书籍的总本书为x,单价为y,那么A类书籍本数为x-2,C类书籍的本数为x+3,A类书籍的单价为y+4,C类书籍的单价为y-4。根据书籍的总开销可以列方程:xy=(x+3)(y-4)xy=(x-2)(y+4)-4,解得x=15,y=24。故一共花了3×24×15+4=1084元。故正确答案为D。考点经济利润问题笔记编辑笔记
55、某次考试100道选择题,每做对一题得1.5分,不做或做错一题扣1分,小李共得100分,那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:A【解析】不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。
56、一个两位数等于其个位数字的平方与十位数字之和,这个两位数是_____。
A: 10B: 76C: 89D: 45
参考答案: C 本题解释:C
57、已知2008年的元旦是星期二,问2009年的元旦是星期几?_____
A: 星期二B: 星期三C: 星期四D: 星期五
参考答案: C 本题解释:正确答案是C考点星期日期问题解析本题需要特别注意的是2008年是闰年,共366天,星期的周期为7,因此用366除以7商52余2,因此2009年元旦的星期数应往后移2天,即星期四,故选择C选项。
58、某单位有员工540人,如果男员工增加30人就是女员工人数的2倍,那么原来男员工比女员工多几人?_____
A: 13B: 31C: 160D: 27
参考答案: C 本题解释:【答案】C。解析:男员工增加30人后,总员工为570人,男员工是女员工的2倍,得女员工为570÷3=190,则原有男员工540-190=350,男员工比女员工多350-190=160人。故正确答案为C。老师点睛:男员工增加30人后,总员工为570人,男员工是女员工的2倍,由于540、30均为偶数,则原有男、女员工的数目也为偶数,男员工比女员工多的人数也是偶数。只有选项C符合条件,故正确答案为C。
59、某公司甲、乙两个营业部共有50人,其中32人为男性。已知甲营业部的男女比例为5:3,乙营业部的男女比例为2:1,问甲营业部有多少名女职员?_____
A: 18B: 16C: 12D: 9
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析设甲营业部有3X名女职员,乙营业部有Y名女职员,则有5X+2Y=32;32+3X+Y=50,解得X=4,Y=6,故甲营业部有3×4=12名女职员,故正确答案为C。秒杀技有题意可知,两个营业部共有50-32=18名女职员,排除A。根据“乙营业部的男女比例为2:1”可知,乙营业部的男职员为偶数,由于男职员的总人数为偶数,则甲营业部的男职员人数同样为偶数。根据“已知甲营业部的男女比例为5:3”,甲营业部的女职员人数能同时被2和3整除,排除B、D,故正确答案为C。
60、41.2×8.1+11×9.25+537×0.19=_____。
A: 527.8B: 536.3C: 537.5D: 539.6
参考答案: C 本题解释:正确答案是C考点计算问题解析41.2×(8+0.1)+(10+1)×9.25+537×(0.2-0.01)=329.6+4.12+92.5+9.25+107.4-5.37=(329.6+107.4)+(4.12+92.5+9.25-5.37)=437+100.5=537.5所以正确答案为C。秒杀技算到第一步的时候可以直接采用尾数法。故0.6+0.12+0.5+0.25+0.4-0.37=1.5,所以选C。标签尾数法
61、小王的手机通讯录上有一手机号码,只记下前面8个数字为15903428。但他肯定,后面3个数字全是偶数,最后一个数字是6,且后3个数字中相邻数字不相同,请问该手机号码有多少种可能? _____
A: 15B: 16C: 20D: 18
参考答案: B 本题解释:答案:B 解析:根据题意,倒数第二个数字有0、2.、4、8四种可能;倒数第三个数字同样有4种可能(只需与倒数第二个数字不同即可),故该手机号为4×4=16种可能。
62、小赵,小钱,小孙一起打羽毛球,每局两人比赛,另一人休息,三人约定每一局的输方下一局休息,结束时算了一下,小赵休息了2局,小钱共打了8局,小孙共打了5局,则参加第9局比赛的是_____。
A: 小钱和小孙B: 小赵和小钱C: 小赵和小孙D: 以上皆有可能
参考答案: B 本题解释:正确答案是B考点统筹规划问题解析本题关键在于三个人打羽毛球,一个人休息的时候必然是另外两个人比赛的时候。因此条件“小赵休息了2局”,说明小钱和小孙对战了2局,则两人其余的比赛都是和小赵进行的,于是总的比赛局数为8+5-2=11局。三人比赛中,任何一个人不可能连续休息两场,也即每个人的休息场次只能是间隔的,而11局比赛中小孙打了5局,休息了6局,那么他只能是这11局中的第2、4、6、8、10局中上场。因此第9局比赛中小孙没有上场,也即参加比赛的是小赵和小钱。故正确答案为B。
63、有20位运动员参加长跑,他们的参赛号码分别是1,2,3,……,20,至少要从中选出多少个参赛号码,才能保证至少有两个号码的差是13的倍数?_____
A: 12B: 15C: 14D: 13
参考答案: C 本题解释:参考答案:C题目详解:将这20个数字分别列为如下:(1,14),(2,15),(3,16),…,(7,20),8,9,10,11,12,13。考虑最差情况,就是前面抽出13个数字就是1-13,然后取第14个数字的时候不管取什么,肯定是14-20中的一个,与前面的数字相减必然能等于13。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
64、甲、乙沿同一公路相向而行,甲的速度是乙的1.5倍,已知甲上午8点经过邮局,乙上午10点经过邮局。问:甲乙在中途何时相遇? _____
A: 8点48分B: 8点30分C: 9点D: 9点10分
参考答案: A 本题解释:A。【解析】设乙的速度为x,甲就是1.5x,当甲8点到邮局时,乙离邮局还有2个小时的路程(2x),甲乙走完2x路程需要2x/(1.5x+x)=4/5小时=48分钟,加上8点,就是8点48分相遇。
65、如果A是质数,而且是个一位数,A+12是质数,同时A+18也是质数,求A是多少?_____
A: 5B: 7C: 9D: 11
参考答案: A 本题解释:参考答案:A题目详解:依题意:A是质数,而且是个一位数,一位数的质数有:2,3,5,7;代入法:5+12=17;18+5=23;5符合条件。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
66、60名员工投票从甲、乙、丙三人中评选最佳员工,选举时每人只能投票选举一人,得票最多的人当选。开票中途累计,前30张选票中,甲得15票,乙得10票,丙得5票。问在尚未统计的选票中,甲至少再得多少票就一定当选?_____
A: 15 B: 13 C: 10 D: 8
参考答案: B 本题解释:【解析】B.最值问题。构造最不利,由题意,还剩30名员工没有投票,考虑最不利的情况,乙对甲的威胁最大,先给乙5张选票,甲乙即各有15张选票,其余25张选票中,甲只要在获得13张选票就可以确定当选。
67、两个圆柱形水井,甲井的水深是乙井的一半,水面直径是乙井的2倍,蓄水量为40立方米,问乙井的蓄水量为多少立方米?_____
A: 20B: 40C: 60D: 80
参考答案: A 本题解释:正确答案是A考点几何问题解析甲井水面直径是乙井的2倍,则水面面积是乙井的4倍,而水深为乙井的一半,因此甲井蓄水体积是乙井的2倍,因此乙井的蓄水量是:40÷2=20立方米,故正确答案为A。
68、某市出租车收费标准是:5千米内起步费10.8元,以后每增加1千米增收1.2元,不足1千米按1千米计费。现老方乘出租车从A地到B地共支出24元,如果从A地到B地先步行460米,然后再乘出租车也是24元,那么从AB的中点C到B地需车费_____元。(不计等候时间所需费用)
A: 12B: 13.2C: 14.4D: 15.6
参考答案: C 本题解释:经济M题。共花钱24元,超过5千米的部分为24-10.8=13.2(元),超过5千米后走了13.2÷1.2=11(千米),总路程最多为16千米,因为步行460米后花费相同,说明460米后的路程一定超过15千米,则总路程15+0.46<S≤16,则C到B的距离7.73<< p>S/2≤8,因不足1千米按1千米计费,故应看成8千米,共花费10.8-9(8-5)×1.2=14.40(元)。
69、定义:①群体互补效应:由不同年龄、专业、智能水平、气质类型的人才有机地组成一个结构合理的人才群体,达到知识互用、能力互补,使只有专才的个体,变成多能的人才群。②群体协调效应:在结构合理的人才群体中,逐步形成了群体每个成员共同遵守的良好的道德规范和传统作风,以此调节和协调群体中个体与个体、个体与群体、群众与社会的关系,并影响和控制整个群体,使群体的力量和功能得到维护和加强。③群体感应效应:在结构合理的人才群体中,人才之间在目标上志同道合,在学风上互相感染,在学术上互相影响,同心同德,紧密团结,创新意识和创造思维不断激化和强化,形成对人才创造特别有利的“微型气候”。典型例证:(1)某大学有效整合资源,在校内外组织多方面人才,团结协作,集体攻关。(2)正因为好大学有优良的校风和传统,所以人人才都想上好大学。(3)小李做事低调,从不张扬。上述典型例证与定义存在对应关系的数目有_____。
A: 0个B: 1个C: 2个D: 3个
参考答案: C 本题解释:【答案】C。解析:第一步:抓住每个定义中的关键词群体互补效应:关键词强调“不同年龄、专业、智能水平、气质类型的人才”、“知识互用、能力互补”。群体协调效应:关键词强调“群体每个成员共同遵守”、“调节和协调”。群体感应效应:关键词强调“目标上志同道合,在学风上互相感染,在学术上互相影响”。第二步:逐一分析例证与定义间的关系例证(1)大学组织了多方面的人才,形成群体互补效应,对应定义①,例证(2)好大学因为有优良的校风和传统而受欢迎,属于群体感应效应,对应定义③;例证(3)讲的是小李的个体行为,与上面的定义均不相符。例证与定义存在对应关系的数目有2个,故正确答案为C。
70、对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有_____。
A: 22人B: 28人C: 30人D: 36人
参考答案: A 本题解释:【答案解析】本题可以使用阴影覆盖法,即100-(40+18+20)=22(人),故远A项。
71、某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人,问今年男员工有多少人?_____
A: 329B: 350C: 371D: 504
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析设去年男员工X人,女员工Y人,由题意知:X+Y=830,5%Y-6%X=3,解得X=350。今年男员工减少了,所以人数小于350,只有A符合条件,故正确答案为A。秒杀技由题知,今年男员工数是去年的94%,所以今年男员工数可被94%整除,根据选项,只有A符合。故正确答案为A。标签数字特性
72、公路上有三辆同向行驶的汽车,其中甲车的时速为63公里,乙、丙两车的时速均为60公里,但由于水箱故障,丙车每连续行驶30分钟后必须停车2分钟。早上10点,三车到达同一位置,问1小时后,甲、丙两车最多相距多少公里?_____
A: 5B: 7C: 9D: 11
参考答案: B 本题解释:正确答案是B考点行程问题解析在这1个小时中,丙车最多休息4分钟,也即丙在一个小时内最少行程为60×56÷60=56公里。而甲车持续行驶,可达63公里。因此两车最多相距7公里,故正确答案为B。
73、三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数_____
A: 48人B: 49人C: 50人D: 51人
参考答案: B 本题解释:【答案】B,列方程即可求解
74、1.31×12.5×0.15×16的值是_____。
A: 39.3B: 40.3C: 26.2D: 26.31
参考答案: A 本题解释:答案:A【解析】本式可写为1.31×12.5×4×0.15×4。
75、某人去A、B、C、D、E五个城市旅游,第一天去A城市,第七天到E城市。如果他今天在某个城市,那么他第二天肯定会离开这个城市去另外一个城市。那么他一共有多少种旅游行程安排的方式?_____
A: 204B: 205C: 819D: 820
参考答案: C 本题解释:参考答案:C题目详解:此题等价于:五个人传六次球;确定M:5;确定N:6;根据“传球问题核心公式”: ;与之最接近的是819,第二接近的是820;因此若第七天回到A城市则有820种方法,去另外一个城市则有819种方法;所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
;与之最接近的是819,第二接近的是820;因此若第七天回到A城市则有820种方法,去另外一个城市则有819种方法;所以,选C。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
76、某次抽奖活动在三个箱子中均放有红、黄、一绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少?_____
A: 在 0~25%之间B: 在25~50%之间C: 在50~75%之间D: 在75~100%之间
参考答案: C 本题解释:C。
77、现有边长1米的一个木质正方体,已知将其放入水里,将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体,并将所有的小正方体都放入水中,直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
78、疾病控制中心,对某校高中三个年级的学生进行抽样做视力状况调查,抽样的方法为分层抽样(按比例抽样)若高中一、二、三年级学生人数分别为626、703、780,样本容量为84,则应从高二年级抽样的学生人数为多少?_____
A: 24B: 26C: 28D: 30
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析根据已知,高中一、二、三年级学生人数分别为626、703、780,所以样本中高二年级应该占的比例为703÷(626+703+780)=1/3,所以样本中高二年级人数为84×1/3=28人。故正确答案为C。秒杀技可以看出703-626=780-703,所以高二年级人数正好占总体的1/3,因此选择84÷3=28。故正确答案为C。
79、一本100多页的书,被人撕掉了4张,剩下的页码总和为8037,则该书最多有多少页?_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析:撕掉一张纸,其正反两面的两个页码之和为奇数,则撕掉4张,页码总数必为偶数,剩余页码和为8037,所以原书的页码总和必然为奇数,由此排除BD(BD选项能被4整除,而连续4页的页码和必然为偶数)。代入C,可知整书的页码总和为(1+138)÷2×138=9591,于是撕掉的页码和为9591-8037=1554,那么撕掉的8页的页码平均值为194.25,显然与最多138页矛盾。故正确答案为A。
80、甲、乙、丙三队要完成A,B两项工程,B工程工作量比A工程的工作量多1/4 ,甲、乙、丙三队单独完成A工程所需时间分别是20天、24天、30天。为了同时完成这两项工程,先派甲队做A工程,乙、丙两队共同做B工程,经过几天后,又调丙队与甲队共同完成A工程,那么,丙队甲队合做了多少天? _____
A: 18B: 15C: 10D: 3
参考答案: D 本题解释:【解析】D。解析:三队完成这项工程一共用了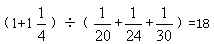 天,乙队一直在做B工程,一共做了
天,乙队一直在做B工程,一共做了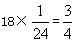 ,则B工程剩下的
,则B工程剩下的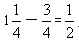 为丙做的,故丙队与乙队合做了
为丙做的,故丙队与乙队合做了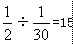 天,与甲队合做了18-15=3天。
天,与甲队合做了18-15=3天。
81、西南赛区四支球队为了争夺小组第一名而进行小组循环赛,已知小马队已比赛了3场,小熊队已比赛了2场,小龙队已比赛了1场,问小牛队比赛了几场_____
A: 3B: 2C: 1
参考答案: B 本题解释:参考答案:B题目详解:小马队已比赛了3场:说明小马队和小熊队、小龙队、小牛队各打了1场;小龙队已比赛了1场:说明小龙队只和小马队比赛了1场;小熊队已比赛了2场:因为和小马队比赛了1场,所以还有1场比赛。因为小龙队只和小马队比赛过,所以小熊队只能和小牛队进行比赛。因此小牛队比赛了2场,分别是和小马队、小熊队进行的比赛。所以,选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
82、某工厂有一大型储水罐供全厂生产用水,已知每天晚8点至早8点蓄水,蓄水管流量为8吨/小时,工厂用水为每天早8点至晚12点,用量为6吨/时,储水罐中水位最高时的储水量至少是_____。
A: 48吨B: 72吨C: 84吨D: 96吨
参考答案: B 本题解释:B【解析】从每晚8点开始蓄水,至早8点水位一直在升高,在这之后,蓄水停止,水位下降;晚8点至晚12点之间,水位上升,但同时仍在用水。故水位最高点应为早8点。8×(12一4)+4×(8一6)=72(吨)。
83、7,77,777,7777……,如果把前77个数相加,那么它们的和的末三位数是多少?_____。
A: 359B: 349C: 329D: 379
参考答案: A 本题解释:【答案】A。解析:把每一个数的末三位相加即可,也即7+77+777×75=58359。
84、一个小于200的数,它除以11余8,除以13余10,那么这个数是多少?_____
A: 118B: 140C: 153D: 162
参考答案: B 本题解释:正确答案是B考点余数与同余问题解析解析1:可直接将4个选项带入,只有B符合题干要求。解析2:根据同余问题口诀”余同取余,和同加和,差同减差,公倍数做周期”,此处符合差同情形,也即除数与余数的差相同,而公倍数为11×13=143,因此被除数的表达式可写为143n-3,符合此表达式的仅B选项。标签直接代入
85、(2005上海,第10题)某单位共有36人。四种血型的人数分别是:A型12人,B型10人,AB型8人,O型6人。如果从这个单位随机地找出两个人,那么这两个人具有相同血型的概率为多少?_____
A: 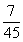 B:
B: 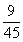 C:
C: 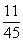 D:
D: 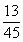
参考答案: C 本题解释:参考答案:C题目详解:从单位找出两个人有: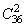 种方法;挑出两种A型血的人有:
种方法;挑出两种A型血的人有: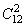 种方法;挑出两种AB型血的人有:
种方法;挑出两种AB型血的人有: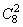 ;种方法;挑出两种O型血的人有:
;种方法;挑出两种O型血的人有: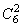 种方法;因此,两个人具有相同血型的概率为
种方法;因此,两个人具有相同血型的概率为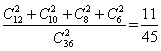 ;所以,选C。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选C。考查点:数量关系>数学运算>概率问题>条件概率
86、圆形的周长扩大至原来的2倍,它的面积比原来增大_____。
A: 1倍B: 2倍C: 3倍D: 4倍
参考答案: C 本题解释:正确答案是C考点几何问题解析 标签几何等比放缩性质
标签几何等比放缩性质
87、任意取一个大于50的自然数,如果它是偶数,就除以2;如果它是奇数,就将它乘3之后再加1。这样反复运算,最终结果是多少? _____
A: 0B: 1C: 2D: 3
参考答案: B 本题解释:【答案】B 解析∶特殊值法,取64,按题意,最后结果为l。也可用排除法,最后结果显然不能为0;若为2,按题意,需再计算一次,得到l;若为3,需继续运算,最后结果也将是1。
88、小明和小红积极参加红领巾储蓄活动,把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品,那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元?_____
A: 44B: 64C: 75D: 86
参考答案: B 本题解释: B【解析】设小明存入银行x元,则小红存入银行(x+20)元。由题意可得:(x-12)×3=(x+20)-12,故x=22。所以两人原来共存入银行22+(22+20)=64(元)。
89、某企业发奖金是根据利润提成的。利润低于或等于10万元时可提成10%,低于或等于20万元时,高于10万元的部分按7.5%提成;高于20万元时,高于20万元的部分按5%提成。当利润额为40万元时,应发放奖金多少万元?_____
A: 2B: 2.75C: 3D: 4.5
参考答案: B 本题解释:【答案】B。解析:40万元的利润,10万元按10%计算利润,10万元按7.5%计算利润,再20万元按5%计算利润。共10×10%+10×7.5%+20×5%=2.75万元。
90、甲、乙、丙三种货物,如果购买甲3件、乙7件、丙1件需花3.15元,如果购买甲4件、乙10件、丙1件需花4.2元,那么购买甲、乙、丙各1件需花多少钱?_____
A: 1.05B: 1.4C: 1.85D: 2.1
参考答案: A 本题解释:正确答案是A考点不定方程问题解析甲×3+乙×7+丙×1=3.15……①甲×4+乙×10+丙×1=4.20……②这是不定方程组,无法解得每个未知数的具体值。换言之,未知数的解存在无穷多个,而题目中四个选项均为确定数值,所以未知数的具体值为多少并不影响甲+乙+丙的值,也即只需要求出其中一组解即可。对此,可以设定最复杂的那个为0,即乙=0,代入后解二元一次方程组,解得甲=1.05,丙=0,即可得甲+乙+丙=1.05。故正确答案为A。秒杀技①×3-②×2可得:甲+乙+丙=3.15×3-4.20×2=1.05。故正确答案为A。
91、市民广场中有两块草坪,其中一块草坪是正方形,面积为400平方米,另一块草坪是圆形,其直径比正方形边长长10%,圆形草坪的面积是多少平方米?_____
A: 410B: 400C: 390D: 380
参考答案: D 本题解释: 【解析】正方形的边长是20米,那么圆的半径是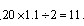 米,那么圆形草坪的面积是
米,那么圆形草坪的面积是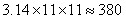 ,故选D。
,故选D。
92、1992是24个连续偶数的和,问这24个连续偶数中最大的一个是几?_____
A: 84B: 106C: 108D: 130
参考答案: B 本题解释:正确答案是B考点数列问题解析解析1:24个连续的偶数是公差为2的等差数列。设最大的偶数为x,则最小的偶数是x-(24-1)×2,由题意得(x+x-23×2)×24÷2=1992,解得x=106,故正确答案为B。解析2:24个连续偶数构成公差为2的等差数列,因此其中位数为1992÷24=83,故最大的数为83+1+(24-13)×2=106,正确答案为B。
93、某大学的文艺社团中,会跳舞的、会吹口琴的会弹古筝的共有38人,其中只会跳舞的有10人,只会吹口琴的有7人,既能弹古筝又会吹口琴的有6人,既会跳舞又会吹口琴的有5人,既会跳舞又会弹古筝的有9人,三种都会的有3人,则只会弹古筝的有多少人?_____
A: 4人B: 6人C: 7人D: 11人
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析解法1:根据已知条件画图分析,有: 于是,只会弹古筝的人数为38-(10﹢6﹢3﹢2﹢7﹢3)=7(人)。故正确答案为C。解法2:由容斥原理,A表示只会一种技能的人数,B表示会两种技能的人数,T表示会三种技能的人数,则由已知条件有:B+3T=6+5+9,T=3,于是B=11;又因A+B+T=38,于是A=38-11-3=24。所以只会弹古筝的人数为24-10-7=7(人),正确答案为C。标签三集合容斥原理公式画图分析
于是,只会弹古筝的人数为38-(10﹢6﹢3﹢2﹢7﹢3)=7(人)。故正确答案为C。解法2:由容斥原理,A表示只会一种技能的人数,B表示会两种技能的人数,T表示会三种技能的人数,则由已知条件有:B+3T=6+5+9,T=3,于是B=11;又因A+B+T=38,于是A=38-11-3=24。所以只会弹古筝的人数为24-10-7=7(人),正确答案为C。标签三集合容斥原理公式画图分析
94、某服装厂生产一种服装,每件的成本是144元,售价是200元。一位服装经销商订购了120件这种服装,并提出:每件服装每降低2元,我就多订购6件。按经销商的要求,这个服装厂售出多少件时可以获得最大的利润,这个最大利润是多少元?_____
A: 124,6912B: 144,6912C: 124,9612D: 144,9612
参考答案: B 本题解释:参考答案:B题目详解:设降低2x元,则订购的总数是 件。总利润是:
件。总利润是: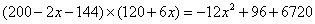 。这个函数是一个开口向下有最大值的抛物线。当
。这个函数是一个开口向下有最大值的抛物线。当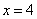 时取得最大值,最大利润6912元。所以,选B。考查点:数量关系>数学运算>利润利率问题>销售数量和售价反向变化引起的最大利润问题
时取得最大值,最大利润6912元。所以,选B。考查点:数量关系>数学运算>利润利率问题>销售数量和售价反向变化引起的最大利润问题
95、教室里有若干学生,走了10名女生后,男生人数是女生的2倍,又走了9名男生后,女生人数是男生的5倍,问最初教室里有多少人?_____
A: 15B: 20C: 25D: 30
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:假设教室里最初有a名女生,有b名男生,那么根据条件:走了10名女生后,男生是女生的2倍,可列出方程式:2(a-10)=b;又走了9名男生后,女生是男生的5倍可知:a-10=5(b-9);联立可得a=15,b=10,所以最初教室里有人数15+10=25人。解析2:走了10名女生后,女生:男生=1:2=5:10;走了9名男生后,女生:男生=5:1,可见男生刚好减少9份,每份1人,则走了9名男生后,男生人数为1人,女生人数为5人,故原有男生10人,女生10+5=15人,所以最初教室里有10+15=25人。故正确答案为C。
96、将三盆同样的红花和四盆同样的黄花摆放成一排,要求三盆红花互不相邻,共有多少种不同的方法?_____
A: 8B: 10C: 15D: 20
参考答案: B 本题解释:B。【解析】四盆黄花两侧可形成5个空隙,要使三盆红花互不相邻只需从中选取3个空隙放入红花即可,=10。
97、小蔡去超市购物,她买了1.6千克苹果、4磅食油和3.8斤芦柑。请问小蔡买的这三种食品最重的是哪一中?_____
A: 苹果B: 食油C: 芦柑D: 三者一样重
参考答案: C 本题解释:参考答案:C题目详解:同时考查运算和单位换算: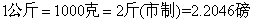 。换算可以得到:小蔡买了约1.814千克食油和1.9千克芦柑;比较1.6、1.814、1.9大小:即可判断出三种食品中芦柑最重;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
。换算可以得到:小蔡买了约1.814千克食油和1.9千克芦柑;比较1.6、1.814、1.9大小:即可判断出三种食品中芦柑最重;所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>比较大小问题
98、有面积为1平方米、4平方米、9平方米、16平方米的正方形地毯各10块,现有面积为25平方米的正方形房间需用以上地毯来铺设,要求地毯互不重叠而且刚好铺满。问最少需几块地毯?_____
A: 6块B: 8块C: 10块D: 12块
参考答案: B 本题解释:正确答案是B考点统筹规划问题解析
99、一道多项选择题有A、B、C、D、E五个备选项,要求从中选出2个或2个以上的选项作为唯一正确的选项。如果全凭猜测,猜对这道题的概率是_____。
A: 1/15B: 1/21C: 1/26D: 1/31
参考答案: C 本题解释:正确答案是C考点概率问题解析
100、某市夏季高峰期对居民用电采用如下办法收取电费:用户月用电量在50度以内的部分,按0.4元/度收费;超过50度的部分,按0.8元/度收费。该市一户居民去年夏季高峰期有一个月的电费为32元,那么这个月该用户用电度数是_____。
A: 50度B: 55度C: 60度D: 65度
参考答案: D