微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、过长方体一侧面的两条对角线交点,与下底面四个顶点连得一四棱锥,则四棱锥与长方体的体积比为多少?_____
A: 1∶8B: 1∶6C: 1∶4D: 1∶3
参考答案: B 本题解释:【答案】B。解析:等底等高时,椎体体积是柱体的1/3。而这里椎体的高是柱体高的一半,因此该四棱锥与长方体的体积之比为1:6,故正确答案为B。
2、学习委员收买练习本的钱,她只记下四组各交的钱,第一组2.61元,第二组3.19元,第三组2.61元.第四组3.48元,又知道每本练习本价格都超过1角,全班共有多少人?_____
A: 29B: 33C: 37D: 41
参考答案: D 本题解释:D。把所有的钱换算成以分为单位的即可。只需要找到261、319和348的超过10的公约数即可,容易得到,这三个数的最大公约数是29,满足题意,因此每本练习本的价格是29分,那么全班有41个人
3、小明每天必须做家务,做一天可得3元钱,做得特别好时每天可得5元钱,有一个月(30天)他共得100元,这个月他有_____天做得特别好。
A: 2B: 3C: 5D: 7
参考答案: C 本题解释:正确答案是C考点鸡兔同笼问题解析设做得好的天数为n,则有5n+3(30-n)=100,解得n=5,故正确答案为C。
4、如图,甲、乙、丙、丁四个长方形拼成正方形EFGH,中间阴影为正方形。已知,甲、乙、丙、丁四个长方形面积的和是32cm2,四边形ABCD的面积是20cm2。问甲、乙、丙、丁四个长方形周长的总和是_____。 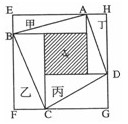
A: 32cmB: 56cmC: 48cmD: 68cm
参考答案: C 本题解释:正确答案是C考点几何问题解析根据已知,四边形ABCD的面积为甲、乙、丙、丁四个长方形面积的一半加上阴影部分小正方形的面积,所以小正方形的面积为20-32×1/2=4,正方形EFGH的面积为32+4=36,边长为6,甲、乙、丙、丁四个长方形周长的总和为2×(EA+AH+HD+DG+GC+CF+FB+BE)=2×6×4=48,故正确答案为C。
5、(2006国家,第49题)某原料供应商对购买其原料的顾客实行如下优惠措施:①-次购买金额不超过1万元,不予优惠; ②-次购买金额超过1万元,但不超过3万元,给九折优惠; ③-次购买金额超过3万元,其中3万元九折优惠,超过3万元部分八折优惠。某厂因库容原因,第-次在该供应商处购买原料付款7800元,第二次购买付款26100元,如果他-次购买同样数量的原料,可以少付多少元?_____
A: 1460元B: 1 540元C: 3780元D: 4360元
参考答案: A 本题解释:参考答案:A题目详解:第-次付款7800元,因此第-次购买的原料价值7800元(不打折);第二次付款26100元,因此第二次购买的原料价值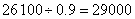 元(打九折);所以两次购买的原料总价值为
元(打九折);所以两次购买的原料总价值为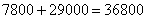 元。①
元。①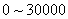 的部分,应付
的部分,应付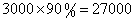 元;②
元;②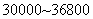 元的部分,应付
元的部分,应付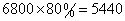 元。综上,总共少支付
元。综上,总共少支付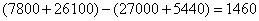 元。考查点:数量关系>数学运算>统筹问题>最优效率分配问题
元。考查点:数量关系>数学运算>统筹问题>最优效率分配问题
6、比-5大-7的数是_____。
A: -3B: 2C: -12D: -7
参考答案: C 本题解释: C [解析] -5+(-7)=-12。故本题选C。
7、一个三位自然数。把它十位上的数字去掉后变成的两位数是原来三位数的七分之一。问这样的三位数有几个?_____
A: 0B: 1C: 2D: 3
参考答案: B 本题解释:B。
8、五人排队甲在乙前面的排法有几种?_____
A: 60B: 120C: 150D: 180
参考答案: A 本题解释: 答案【A】
9、甲乙两人相约见面,并约定第一人到达后,等15分钟不见第二人来就可以离去。假设他们都在10点至10点半的任一时间来到见面地点,则两人能见面的概率有多大?_____
A: 37.5%B: 50%C: 62.5%D: 75%
参考答案: D 本题解释:答案:D.[解析]本题为概率类题目。假设甲、乙分别在0-30分钟之内到达约会地点的情况如下图,则只有在阴影部分区域甲乙能够相遇,也就是求阴影部分面积的比例。很容易看出,阴影部分的面积为3/4=75%。
10、某商店实行促销手段,凡购买价值200元以上的商品可以优惠20%,那么用300元钱在该商店最多可买下价值_____元的商品。
A: 350元B: 384元C: 375元D: 420元
参考答案: C 本题解释:正确答案是C考点经济利润问题解析根据题意列算式:300÷(1-20%)=375。故正确答案为C。
11、六年级某班学生中有1/16的学生年龄为13岁,有3/4的学生年龄为12岁,其余学生年龄为11岁,这个班的平均年龄是:_____
A: 10.02B: 11.17C: 11.875D: 11.675
参考答案: C 本题解释:参考答案:C题目详解:应用方程法:设这个班的人数是x人,则这个班的平均年龄为: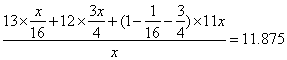 岁。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>加权平均值
岁。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>平均值问题>加权平均值
12、参加某部门招聘考试的共有120人,考试内容共有6道题。1至6道题分别有86人,88人,92人,76人,72人和70人答对,如果答对3道题或3道以上的人员能通过考试,那么至少有多少人能通过考试?_____
A: 50B: 61C: 75D: 80
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析由题意,一共做题120×6=720人次,分别答对1至6题的共有86+88+92+76+72+70=484人次,则没有答对1至6题的人次为720-484=236,当236人次中每人都答错4道题时,未通过考试的人数会最多,通过考试的人会最少,因此未通过考试的人最多为236÷4=59(人),通过考试的人数至少为有120-59=61(人),故正确答案为B。标签逆向考虑
13、有7个不同的质数,他们的和是58,其中最小的质数是多少?_____。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析:除了2以外的质数全是奇数,如果7个数全是奇数的话,他们的和不会是58这个偶数,所以,7个数中必然有2,而2是所有质数中最小的一个。(2、3、5、7、11、13,17这7个质数的和为58)
14、10个人欲分45个苹果,已知第一个人分了5个,最后一人分了3个,则中间的8人一定存在连续的两人至少分了多少个苹果?_____
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:【答案】C。解析:中间的8人共分得苹果45-5-3=37(个),将中间的8人分为4组,即(第2、3个人)(第4、5个人)(第6、7个人)(第8、9个人)。由37=9×4+1可知,必有1组,即连续的两人分到了10个苹果。故答案为C。
15、五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩,其中语文成绩优秀的有65人,数学成绩优秀的有87人。语文、数学都优秀的有多少人?_____
A: 30B: 35C: 57D: 65
参考答案: A 本题解释:参考答案:A题目详解:此题是典型的两个集合的容斥问题,由题意设:A={{语文成绩优秀的人}};B={{数学成绩优秀的人}};因此,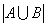 ={{五年级参加语文、数学考试的人}};
={{五年级参加语文、数学考试的人}}; ={{语文和数学都优秀的人}}由两个集合的容斥原理可得:
={{语文和数学都优秀的人}}由两个集合的容斥原理可得: =
=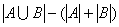 =
=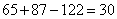 所以,选A。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
所以,选A。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
16、在一个老年活动中心,会下象棋的有59人,会下围棋的有48人,两种棋都不会下的有12人,两种棋都会下的有30人,问这个俱乐部一共有多少人?_____
A: 89人B: 107人C: 129人D: 137人
参考答案: A 本题解释:正确答案是A考点容斥原理问题解析根据两集合容斥原理,设该俱乐部总人数为a,则59+48-30=a-12,解得a=89(人),故正确答案为A。注:两集合容斥原理推论公式:满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。
17、某村有甲乙两个生产小组,总共50人,其中青年人共13人。甲组中青年人与老年人的比例是2∶3,乙组中青年人与老年人的比例是1∶5,甲组中青年人的人数是:_____
A: 5人B: 6人C: 8人D: 12人
参考答案: C 本题解释:【答案】C。解析:设甲组人数为5x,乙组人数为6y。有,解得x=4。因此甲组青年人的人数为8。
18、从1、2、3、4中任取3个数组成没有重复的三位数的偶数的取法种数为_____。
A: 10 B: 12 C: 13 D: 11
参考答案: B 本题解释:【解析】B。 题干要求组成没有重复数字的三位数的偶数,所以只有尾数是2或4两种情况。当尾数是2时,有2×3=6(种);当尾数是4时,有2×3=6(种),所以共有6+6=12(种),故本题答案为B。
19、某人沿电车线路匀速行走,每12分钟有一辆电车从后面追上,每4分钟有一辆电车迎面开来。假设两个起点站的发车间隔是相同的,求这个发车间隔。_____
A: 2分钟B: 4分钟C: 6分钟D: 8分钟
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:本题关键是能够发掘出“相邻两车之间的距离是相等的”这一隐藏条件,即无论从后面来的车,还是前面来的车,相邻两车的距离相等。设相邻两车的距离为60,车的速度为x,人的速度为y,根据题意得:x+y=60/4,x-y=60/12,联立解得x=10,y=5,因此发车间隔为:60÷10=6,故选择C选项。 标签双向数车模型赋值思想公式应用
标签双向数车模型赋值思想公式应用
20、(2005国家,第38题) 的末位数字是_____。
的末位数字是_____。
A: 1B: 3C: 7D: 9
参考答案: A 本题解释:参考答案:A题目详解:应用首尾数法: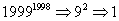 所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>首尾数法
21、某厂生产一批商标,形状为等边三角形或等腰三角形。已知这批商标边长为2cm或4cm,那么这批商标的周长可能是_____。
A: 6cm12cmB: 6cm8cm12cmC: 6cm10cm12cmD: 6cm8cm10cm12cm
参考答案: C 本题解释:正确答案是C考点几何问题解析三角形的两边之和必须大于第三边,因此三边可能有三种情况:(2,2,2)、(2,4,4)、(4,4,4),周长为分别为6cm、10cm、12cm,故正确答案为C。
22、一种溶液,蒸发掉一定量的水后,溶液的浓度为10%;再蒸发掉同样多的水后,溶液的浓度变为12%;第三次蒸发掉同样多的水后,溶液的浓度将变为多少?_____
A: 14%B: 17%C: 16%D: 15%
参考答案: D 本题解释:正确答案是D考点浓度问题解析在蒸发的过程中,溶液的量发生变化,但其中溶质保持不变,因此将溶质作为解题突破口,给溶质赋值。为方便后面的计算,设其溶质为60,则可知其浓度在10%时,溶液量为600,其浓度在12%时,溶液量为500。这说明在变化过程中蒸发掉了水为100。因此第三次蒸发同样多的水后,溶液还剩400,故其浓度为15%。故正确答案为D。标签赋值思想
23、一根钢管,如果把它锯成4段,需要24分钟。照此速度,如果将它锯成8段,需要多长时间?_____
A: 42分钟B: 48分钟C: 56分钟D: 64分钟
参考答案: C 本题解释:【答案】C。解析:把一根钢管锯成4段有3个切口,并且需要24分钟,一个切口需要8分钟。若将它锯成8段,将有7个切口,则一共需要7×8=56分钟。故正确答案为C。
24、有一本畅销书,今年每册书的成本比去年增加了10%,因此每册书的利润下降了20%,但是今年的销量比去年增加了70%。则今年销售该畅销书的总利润比去年增加了_____。
A: 36%B: 25%C: 20%D: 15%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析假设每册书利润为10元,去年销量为10册,则今年每册书的利润为8元,销量为17册。因此去年的总利润为10×10=100元,今年的总利润为8×17=136元,因此今年销售该畅销书的总利润比去年增加了36%。正确答案为A。
25、地上放着一个每一面上都有一个数的六面体箱子,对面两个数的和均为27。甲能看到顶面和两个侧面,这三个面上的数字之和是35;乙能看到顶面和另外两个侧面,且这三个面上的数字和为47。箱子贴地一面的数字是:_____
A: 14B: 13C: 12D: 11
参考答案: B 本题解释:参考答案:B题目详解:先求出顶面的数字:甲、乙二人看到的数加起来一共为:2组对面加上2倍的顶面数字;则顶面的数字为:(35+47-27×2)÷2=14;根据对面两个数的和均为27:底面的数字为: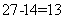 ;所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
;所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
26、长为1米的细绳上系有一个小球,从A处放手以后,小球第一次摆到最低点B处共移动了多少米?_____
A: 1+(1/3)πB: 1/2+(1/2)πC: (2/3)πD: 1+(2/3)π
参考答案: A 本题解释:正确答案是A考点几何问题解析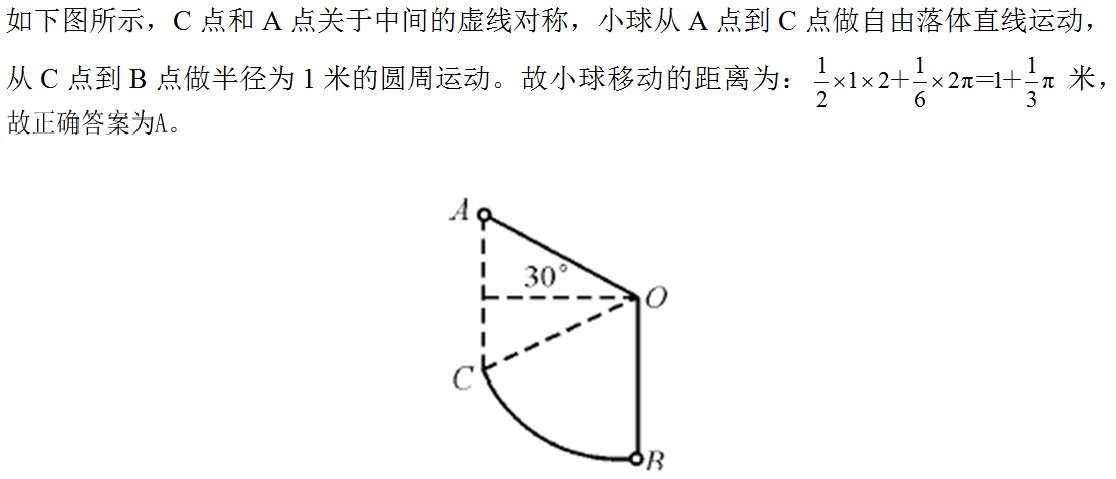 备注:本题中所求长度的线条即有线段与圆弧两部分组成,正确把握分界点是解题关键。考题中的分界点一般与物理常识相关。
备注:本题中所求长度的线条即有线段与圆弧两部分组成,正确把握分界点是解题关键。考题中的分界点一般与物理常识相关。
27、一列长90米的火车以每秒30米的速度匀速通过一座长1200米的桥,所需时间为_____。
A: 37秒B: 40秒C: 43秒D: 46秒
参考答案: C 本题解释:C【精析】火车过桥实际走过的距离等于火车的长度加上桥的长度,因此所需时间=(1200+90)÷30=43(秒)。
28、已知甲、乙两人共有260本书,其中甲的书有13%是专业书,乙的书有12.5%是专业书,问甲有多少本非专业书?_____
A: 75B: 87C: 174D: 67
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析由“甲的书有13%是专业书”可知,甲的专业书=甲的书×13%,所以甲的书是100的倍数,甲的非专业书是87的倍数,排除A、D。由“乙的书有12.5%是专业书”可知,乙的专业书=乙的书×12.5%=乙的书×1/8,所以乙的书是8的倍数。结合选项,若甲的专业书为174本,则甲有200本书,那么乙的书有60本,不是8的倍数,排除C,故正确答案为B。标签数字特性
29、在一个大笼子里关了一些鸡和一些兔子。数它们的头,一共有36个;数它们的腿一共有100条。问鸡和兔各多少只_____
A: 鸡21只,兔13只B: 鸡23只,兔16只C: 鸡22只,兔14只D: 鸡23只,兔15只
参考答案: C 本题解释:参考答案:C题目详解:假设36只全是鸡,就应有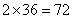 条腿,这就比题目所说的“100条腿”少了28条腿。为什么“腿”会少呢?很显然,是我们把四条腿的兔子当成了两条腿的鸡。由此即可求出兔子的只数,列式为:
条腿,这就比题目所说的“100条腿”少了28条腿。为什么“腿”会少呢?很显然,是我们把四条腿的兔子当成了两条腿的鸡。由此即可求出兔子的只数,列式为: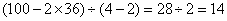 (只);鸡的只数为:
(只);鸡的只数为: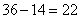 (只)。因此,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>基本鸡兔同笼问题
(只)。因此,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>基本鸡兔同笼问题
30、现有边长1米的一个木质正方体,已知将其放入水里,将有0.6米浸入水中。如果将分割成边长0.25米的小正方体,并将所有的小正方体都放入水中,直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:本题属于面积问题。因为把边长为1米的正方体木块置于水中有0.6米浸入水中,所以当将其分割为边长0.25米的正方体木块置于水中时,其浸入水中的高度为3/20米。则可以计算出其中一个分割后的正方体木块与水的接触面积为:(1/4)×(1/4)+4×(1/4)×(3/20)=1/16+3/20,又因为边长1米的正方体可以分割为64个边长为O.25米的正方体,所以题中所求面积为:64×(1/16+3/20)=13.6(平方米)。正确答案为C。
31、小明和小强参加同一次考试,如果小明答对的题目占题目总数的3/4,小强答对了27道题,他们两人都答对的题目占题目总数的2/3,那么两人都没有答对的题目共有_____。
A: 3道B: 4道C: 5道D: 6道
参考答案: D 本题解释:正确答案是D考点容斥原理问题解析由“小明答对的题目占题目总数的3/4”,可知题目总数是4的倍数;由“他们两人都答对的题目占题目总数2/3”,可知题目总数是3的倍数。因此,题目总数是12的倍数。小强做对了27题,超过题目总数的2/3,则题目总数是36。根据两集合容斥原理公式得两人都没有答对的题目共有36-(36×3/4+27-36×2/3)=6道,故正确答案为D。
32、一块试验田,以前这块地所种植的是普通水稻。现在将该试验田的1/3种上超级水稻,收割时发现该试验田水稻总产量是以前总产量的1.5倍。如果普通水稻的产量不变,则超级水稻的平均产量与普通水稻的平均产量之比是_____。
A: 5∶2B: 4∶3C: 3∶1D: 2∶1
参考答案: A 本题解释:答案:A。设该试验田种普通水稻产量为x,种超级水稻产量为y,则有,解得y∶x=5∶2。
33、(2004山东)某次测验有50道判断题,每做对一题得3分,不做或做错一题倒扣1分,某学生共得82分,问答对题数和答错题数(包括不做)相差多少?_____
A: 33B: 39C: 17D: 16
参考答案: D 本题解释:参考答案 题目详解:设答对题数为
题目详解:设答对题数为 ,答错题数(包括不做)为
,答错题数(包括不做)为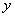 ;列方程得:
;列方程得: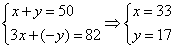 ;所以答对题数和答错题数(包括不做)相差为16。所以,选D。考查点:数量关系>数学运算>盈亏问题
;所以答对题数和答错题数(包括不做)相差为16。所以,选D。考查点:数量关系>数学运算>盈亏问题
34、某俱乐部中女会员的人数比男会员的一半少61人,男会员的人数比女会员的3倍多2人,问该俱乐部共有会员多少人?_____
A: 475人B: 478人C: 480人D: 482人
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析设女会员有X人,男会员为Y人,则有0.5Y-61=X,3X+2=Y,解得X=120,Y=362,总人数为120+362=482。故正确答案为D。秒杀技由题目第一个条件可知会员总数加上61后能被3整除,也即加上1后能被3整除,仅选项D符合。标签数字特性
35、一队战士排成三层空心方阵多出9人,如果在空心部分再增加一层,又差7人,问这队战士共有多少人?_____
A: 121B: 81C: 96D: 105
参考答案: D 本题解释:D[解一]由题意可得空心方阵再往里一层的总人数是:9+7=16(人),每边人数为:16÷4+1=5(人);所以3层空心方阵最外层每边人数为:5+2×3=11(人),总人数为:(11-3)×3×4=96(人);这队战士的总人数是:96+9=105(人)。[解二]相邻两层的人数之差为8人,最里层的人数为9+7+8=24人,次里层为24+8=32人,最外层为32+8=40人,所以总人数为24+32+40+9=105人。
36、福州大洋百货为了庆祝春节,特举行让利百万大酬宾促销活动,在二楼打出了买300送60元的优惠活动。其中某柜台各以3000元卖出两件商品,其中盈亏均为 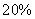 ,则该柜台应_____。
,则该柜台应_____。
A: 赚500元B: 亏300元C: 持平D: 亏250元
参考答案: D 本题解释:参考答案 题目详解:本题中的买300送60是迷惑条件,无用。售价都是3000,总共收入:3000×2=6000元;以3000元卖出商品的成本分别为:3000÷1.2=2500,3000÷0.8=3750;卖出这两件商品,该柜台利润为:3000×2-(3750+2500)=-250元。所以,选D。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
题目详解:本题中的买300送60是迷惑条件,无用。售价都是3000,总共收入:3000×2=6000元;以3000元卖出商品的成本分别为:3000÷1.2=2500,3000÷0.8=3750;卖出这两件商品,该柜台利润为:3000×2-(3750+2500)=-250元。所以,选D。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
37、某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售,由于定价过高,无人购买,后来不得不按38%的利润重新定价,这样出售了其中的40%。此时,因害怕剩余水果腐烂变质,不得不再次降价,售出了剩余的全部水果。结果,实际获得的总利润是原定利润的30.2%,那么第二次降价后的价格是原定价的_____。
A: 75%B: 50.%C: 62.5%D: 45%
参考答案: C
38、某管理局车库里有6个油桶,分别盛有汽油、柴油和机油。其重量为31升、20升、19升、18升、16升、15升。已知六桶油中有一桶汽油,柴油的重量比机油多一倍。请问柴油是多少?_____
A: 49升B: 50升C: 66升D: 68升
参考答案: C 本题解释:参考答案:C本题得分:题目详解:柴油的重量比机油多一倍,则柴油和机油的总升数能被3整除:所以各个柴油桶、机油桶升数分别除以3的余数之和能被3整除;31、20、19、18、16、15除以3余数分别为1、2、1、0、1、0,只有在第二桶20升的是汽油的情况下,剩下的5桶才可能出现柴油比机油多一倍的情况,则剩下的5桶和为99升,柴油比机油多一倍;因此,柴油为66升;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
39、地球表面的陆地面积和海洋面积之比是29︰71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系,可以推断出南、北半球的海洋面积之比为: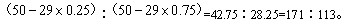
40、(2006江苏,第9题) 的值为_____。
的值为_____。
A:  B:
B: 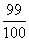 C:
C:  D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:可以化成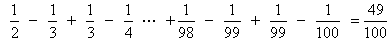 (该解析由用户“asdsds”于2010-08-2018:52:08贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
(该解析由用户“asdsds”于2010-08-2018:52:08贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
41、某班共有50名学生参加数学和外语两科考试,已知数学成绩及格的有40人,外语成绩及格的有25人,据此可知数学成绩及格而外语成绩不及格者_____。
A: 至少有10人B: 至少有15人C: 有20人D: 至多有30人
参考答案: B 本题解释:B【解析】这是一个集合问题,首先可排除答案D,因为与已知条件“外语及格25人”即“外语不及格25人”不符;其次排除C,因为仅以外语及格率为50%推算数学及格者(40人)中外语不及格人数为40×50%=20(人),缺乏依据,实际上,数学及格者中外语不及格的人数至少为25-(50-40)=15人,答案为B。
42、某原料供应商对购买其原料的顾客实行如下优惠措施:①一次购买金额不超过1万元,不予优惠;②一次购买金额超过1万元,但不超过3万元,给九折优惠;③一次购买金额超过3万元,其中3万元九折优惠,超过3万元部分八折优惠。某厂因库容原因,第一次在该供应商处购买原料付款7800元,第二次购买付款26100元,如果他一次购买同样数量的原料,可以少付:_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元,原料的总价值应为7800元,第二次购买时付款26100元,原料的总价值应为26100÷0.9=29000元。如果要将两次购买变成一次购买,则总价值应为7800+29000=36800元,而应该付款额为30000×0.9+6800×0.8=32440元,一次性购买比分两次购买可以节约7800+26100-32440=1460元。
43、甲乙两人从相距1350米的地方,以相同的速度相对行走,两人在出发点分别放下1个标志物。再前进10米后放下3个标志物。前进10米放下5个标志物,再前进10米放下7个标志物,以此类推。当两个相遇时,一共放下了几个标志物?_____
A: 4489B: 4624C: 8978D: 9248
参考答案: D 本题解释:正确答案是D考点数列问题解析以10米为间隔,可知1350米的路程被分成135个间隔,因此共有136个放标志物的点,按甲乙平分为两组,每组为68个点,故甲或乙最后均放置135个标志物。由求和公式可知总数为(1+135)÷2×68×2=9248。因此正确答案为D。注:等差数列求和公式,和=(首项+末项)×项数÷2秒杀技易知全程被分为135个间隔,从而得出每组放置标志物的点为偶数,注意到每次放下标志物都为奇数,从而可知每组的标志物总数必然为偶数。又考虑到甲乙两组是相同的,而选项中C、D分别为A、B的两倍,而A、B中B为偶数,故可猜测B为一人放下的标志物数,而D为答案。标签猜题技巧
44、(2006江苏,第9题)算式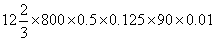 的值是_____。
的值是_____。
A: 312B: 348C: 570D: 286
参考答案: C 本题解释:参考答案:C题目详解:应用因式分解法:原式 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
45、一个自然数被6除余4,被8除余6,被10除余8,那么这个数最小为多少?_____
A: 58B: 66C: 118D: 126
参考答案: C 本题解释:参考答案:C题目详解:此题为剩余定理中差同的情况。根据"差同减差,最小公倍数做周期"可知:这个自然数加上2以后,就能够被6、8和10整除;而6、8和10的最小公倍数是120:因此,这个数最小为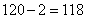 。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
。所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
46、某商店,雨天每天售出雨伞30把,晴天每天售出雨伞12把,连续数天平均每天售出16把雨伞,共售出144把,晴天有_____天。
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:售出雨伞的总天数为:144÷16=9天,假设全是雨天售出的,则雨伞数应该为:30×9=270,这比实际多算了270-144=126。这些是把晴天售出的伞都算成雨天的了,雨天比晴天每天多售出的雨伞数为:30-12=18,那么晴天有: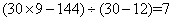 天。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
天。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
47、某三年制普通初中连续六年在校生人数为X1、X2、X3、X4、X5、X6,假设该校所有学生都能顺利毕业,那么前三年的入学学生总数与后三年的入学学生总数之差为_____。
A: 42B: 48C: 50D: 60
参考答案: C 本题解释:正确答案是D考点和差倍比问题解析设原来B桶有x公斤水,A桶有(108-x)公斤水,可得[x+(108-x)×1/4]×(1-1/4)=108÷2,解得x=60。故正确答案为D。秒杀技观察选项设置,B+D=108,可初步确定答案为48或60;而A桶显然不能是60,因为60的四分之一为15,第二次取水会出现小数,此时二者必然不相等,故可确定答案为D。
48、小明和小强从400米环形跑道的同一点出发,背向而行。当他们第一次相遇时,小明转身往回跑;再次相遇时,小强转身往回跑;以后的每次相遇分别是小明和小强两人交替调转方向。小明每秒跑3米,小强每秒跑5米,则在两人第30次相遇时。小明共跑了多少米? _____
A: 11250B: 13550C: 10050D: 12220
参考答案: A 本题解释:A。两人相向运动,经过400÷(3+5)=50秒相遇,之后小明转身,两人做追及运动,经过400÷(5-2)=200秒第二次相遇;接着两人又做相向运动,经过50秒相遇,再做追及运动,经过200秒相遇,以此类推,第30次相遇共用30÷2×(50+200)=3750秒,则小明共跑了3×3750=11250米。
49、甲班有42名学生,乙班有48名学生,在某次数学考试中按百分制评卷,评卷结果两个班的数学总成绩相同,平均成绩是整数,且都高于80分,请问甲班的平均分与乙班相差多少分呢?_____
A: 12分B: 14分C: 16分D: 18分
参考答案: A 本题解释:参考答案:A题目详解:假设甲乙两班平均分分别为x、y,则: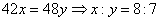 ,不妨假设x=8t,y=7t,则两班平均分相差为t:由题干已知,我们可以得到:
,不妨假设x=8t,y=7t,则两班平均分相差为t:由题干已知,我们可以得到: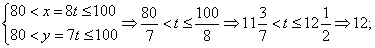 所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
50、张先生向商店订购某种商品80件,每件定价100元。张先生向商店经理说:“如果你肯减价,每减1元,我就多订购4件。”商店经理算了一下,如果减价5%,由于张先生多订购,仍可获得与原来一样多的利润。则这种商品每件的成本是_____。
A: 75元B: 80元C: 85元D: 90元
参考答案: A 本题解释:【解析】A。设成本为x元。减价5%即减去了5元,同样就要多购买4×5=20件,利润相同,即可得到等式(100-x)×80=(95-x)×(80+20),得x=75。
51、某公司要买100本便签纸和100支胶棒,附近有两家超市。A超市的便签纸0.8元一本,胶棒2元一支且买2送1。B超市的便签纸1元一本且买3送1,胶棒1.5元一支,如果公司采购员要在这两家超市买这些物品,他至少要花多少元钱?_____
A: 183.5B: 208.5C: 225D: 230
参考答案: B 本题解释:正确答案是B考点经济利润问题解析先考虑便签,A超市0.8元一本,而B超市3元4本(平均每本0.75元),因此100本便签可全部在B超市购买,花费25×3=75元。再考虑胶棒,A超市为4元3支(平均每支为1.33元),B超市为1.5元一支,因此胶棒尽可能多的在A超市购买,可购买99支,花费99÷3×4=132元,剩余的一支改在B超市购买,花费1.5元。总共需要75+132+1.5=208.5元。因此正确答案为B。
52、2005年7月1日是星期五,那么2008年7月1日是星期几_____
A: 星期三B: 星期四C: 星期五D: 星期二
参考答案: D 本题解释:正确答案是D考点星期日期问题解析2005,2006,2007都是平年(365天),2008是闰年(366天),365=52×7+1,所以,经历一个平年(365天),星期往后推一天,366=52×7+2,所以,经历一个闰年(366天),星期往后推两天,因为2005年7月1日是星期五,所以2008年7月1日是星期五+1+1+2=星期日+2=星期二。故正确答案为D。标签差异分析
53、右图是由5个相同的小长方形拼成的大长方形,大长方形的周长是88厘米,问大长方形的面积多少平方厘米?_____ 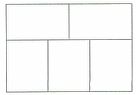
A: 472平方厘米B: 476平方厘米C: 480平方厘米D: 484平方厘米
参考答案: C 本题解释:参考答案:C题目详解:观察大长方形的上下两边,可知:小长方形的长宽比为3:2;设小长方形长宽分别为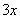 、
、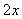 :则周长
:则周长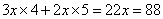 ,
,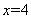 ,即大长方形的长为:
,即大长方形的长为: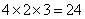 ;宽为:
;宽为: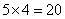 大长方形的面积为:
大长方形的面积为: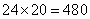 (平方厘米);所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
(平方厘米);所以,选C。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
54、有一个93人的参观团,其中男47人,女46人。他们住进一个旅馆内,旅馆内有可住11人、7人、4人的3种房间。要求男、女分住不同房间,且每个房间均住满,至少需要多少房间?_____
A: 11B: 10C: 13D: 17
参考答案: A 本题解释: A 解析: 设男的安排11人房间a间,7人房间b间,4人房间c间。则应满足等式11a+7b+4c=47。在这个等式中,a取尽量大的值a=3,b取最大值2,c取0。因此男的至少安排房间数为3+2+0=5(间);设女的安排11人房间d间,7人房间e间,4人房间f间,则有11d+7e+4f=46。经试验不难看出,d=1,e=5,f=0。因此女的至少安排房间数为1+5+0=6(间)。总共至少安排房间:5+6=11(间)。故本题选A。
55、一个生产队的粮食产量,两年内从60万斤增加到79.35万斤,问平均每年增长百分之几?_____
A: 15%B: 20%C: 10%D: 25%
参考答案: A 本题解释:正确答案是A考点和差倍比问题解析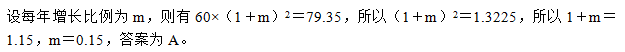
56、甲、乙、丙三人买水果,甲买了3千克苹果和2千克梨,乙买了4千克苹果和3千克梨,丙买了3千克苹果和4千克梨。乙比甲多花7元,甲比丙少花5元。问甲、乙、丙共花了多少钱?_____。
A: 92.5元B: 112.5元C: 88.0元D: 67.5元
参考答案: D
57、甲、乙、丙三辆车的时速分别为60公里、50公里和40公里,甲从A地,乙和丙从B地同时出发相向而行,途中甲遇到乙后15分钟又遇到丙,问A、B两地相距多少公里?_____
A: 150公里B: 250公里C: 275公里D: 325公里
参考答案: C 本题解释:正确答案是C考点行程问题解析解析1:甲乙相遇时,甲走了全程的60÷(50+60)=6/11;甲丙相遇时,甲走了全程的60÷(40+60)=6/10;在甲乙相遇之后到甲丙相遇,甲走了全程的6/10-6/11=3/55,这段路程为60×15/60=15(公里),所以AB相距15÷(3/55)=275(公里)。解析2:设AB相距s公里,则s/(60+50)=s/(60+40)-1/4,解得s=275(公里)。故正确答案为C。
58、某水果店到苹果产地去收购苹果,收购价为0.84元/千克,从产地到水果店距离200千米,每吨每运1千米运费为1.20元。如果在运输及销售过程中的损耗是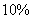 ,商店想要实现
,商店想要实现 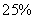 的利润,零售价应是_____。
的利润,零售价应是_____。
A: 1.50元/千克B: 1.45元/千克C: 1.40元/千克D: 1.35元/千克
参考答案: A 本题解释:参考答案:A题目详解:解法一:每千克苹果的成本为: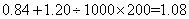 元;零售价应为:
元;零售价应为: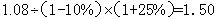 元/千克.解法二:特例法假设收购1吨苹果,收购价840元,运费
元/千克.解法二:特例法假设收购1吨苹果,收购价840元,运费 元,损耗10%,也就是剩下的0.9吨要实现25%利润,则:
元,损耗10%,也就是剩下的0.9吨要实现25%利润,则: ,即1350是水果全部卖出后的总价。零售价应为:
,即1350是水果全部卖出后的总价。零售价应为: 元/千克所以,选A。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
元/千克所以,选A。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
59、已知29832983…298302能被18整除,那么n的最小值是_____。
A: 4B: 5C: 6D: 7
参考答案: A 本题解释:【解析】18=2×9,这个多位数的个位上是2,满足被2整除,因此,只需考虑个位数字之和能否被9整除的问题。(2+9+8+3)×n+0+2=22n+2是9的倍数,22×4+2=90=9×10,那么n的最小值为4。
60、某村有甲乙两个生产小组,总共50人,其中青年人共13人。甲组中青年人与老年人的比例是2:3,乙组中青年人与老年人的比例是1:5,甲组中青年人的人数是_____。
A: 5人B: 6人C: 8人D: 12人
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析解析1:由题意可知,甲组青年人占甲组总人数的2/5,乙组青年人占乙组总人数的1/6,假设甲组青年人人数为x,则乙组青年人人数为13-x,列出方程,可得x÷2/5+(13-x)÷1/6=50,解得x=8,则甲组青年人人数为8人。故正确答案为C。解析2:由题意可知,甲组青年人占甲组总人数的2/5,乙组青年人占乙组总人数的1/6,因此甲组人数比能被5整除,乙组人数比能被6整除。而乙组人数又等于50减去甲组人数,因此乙组人数也能被5整除,满足这个条件的,只有甲组为20人,乙组为30人,甲组中青年人的人数为20×2/5=8。故正确答案为C。标签数字特性
61、小明和小红积极参加红领巾储蓄活动,把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品,那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元?_____
A: 44B: 64C: 75D: 86
参考答案: B 本题解释:【答案】B。解析:设小明原来存了Y元,则小红存了Y+20元,根据题意得(Y-12)×3=(Y+20-12),解得Y=22元。因此两人原来共存了2Y+20=64元,故正确答案为B。
62、小明和姐姐用2013年的台历做游戏,他们将12个月每一天的日历一一揭下,背面粘上放在一个盒子里、姐姐让小明一次性帮她抽出一张任意月份的30号或者31号。问小明一次至少应抽出多少张日历,才能保证满足姐姐的要求?_____
A: 346B: 347C: 348D: 349
参考答案: C 本题解释:正确答案是C考点抽屉原理问题解析本题为抽屉原理问题,结果应为最不利情形所抽张数加上1。2013年是平年,共365天,31天的月份有7个,30天的月份有4个,则至少需要抽出365-7×2-4+1=348张。故正确答案为C。
63、在前100个自然数中,能被3除尽的数相加,所得到的和是多少?_____
A: 1250B: 1683C: 1275D: 1400
参考答案: B 本题解释:参考答案:B本题得分:题目详解:根据题意,在前100中,能被3除尽的数,即个位数字之和为3的倍数;“在前100个自然数中,能被3整除的数”有3、6、9、12、15、18……故可以转化为首项为3,末项为99,公差为3,共有33项的等差数列;在前100个自然数中,能被3除尽的数的和——等差数列求和: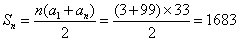 所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
所以,选B。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
64、一排长椅共有90个座位。其中一些座位已经有人就座了。这时,又来了一个人要坐在这排长椅上,有趣的是,他无论坐在哪个座位上都与已经就座的某个人相邻。原来至少有多少人已经就座?_____
A: 3lB: 30C: 29D: 32
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据题意:可推知这排长椅上已经就座的任意相邻的两人之间都有两个空位;已经就座的人最左边一个(最右边一个)既可以坐在左边…边)起第一个座位上,也可以坐在左边(右边)起第二个座位上(如图所排…的两种情况,“●”表示已经就座的人,“○”表示空位)。(1)●○○●○○●…(2)○●○○●○○●○……题目中问“至少”有多少人就座:那就应选第二种情况,每三人(○●○)一组,所以共有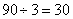 人。所以,选B。解法二:已经就坐的人占据的座位应该为第2,5,8.....:组成一个公差为3等差数列;即第
人。所以,选B。解法二:已经就坐的人占据的座位应该为第2,5,8.....:组成一个公差为3等差数列;即第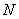 个人占据第
个人占据第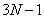 个座位时新来的人无论坐哪个座位上都与已经就坐的某个人相邻且
个座位时新来的人无论坐哪个座位上都与已经就坐的某个人相邻且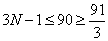 因为人数只能取整数所以
因为人数只能取整数所以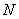 最大取30;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
最大取30;所以,选B。考查点:数量关系>数学运算>排列组合问题>常规排列组合问题
65、某试卷共25题,答对的,一题得4分;答错或不答的,一题扣1分,小王得了60分,则小王答对了多少题?_____
A: 14B: 15C: 16D: 17
参考答案: D 本题解释: D [解析] 设答对了x道题,则未答对的题为(25-x)题,可得4x-(25-x)×1=60,解得x=17。故本题选D。
66、两列火车同向而行,甲车每小时行54千米,乙车每小时行72千米。甲车上一乘客发现:从乙车车头经过他的车窗时开始到乙车车尾经过他的车窗共用了70秒,乙车的车长是_____米。
A: 700B: 400C: 300D: 350
参考答案: D 本题解释:正确答案是D考点行程问题解析甲车的速度是54千米/小时=15米/秒,乙车的速度为72千米/小时=20米/秒。该运动过程实际是乙车车尾与该乘客的追及过程,追及距离为乙车的车长。因此乙车的车长为(20-15)×70=350米,故正确答案为D。公式:追及问题。追及距离=(大速度-小速度)×追及时间。标签公式应用
67、有甲、乙两个项目组。乙组任务临时加重时,从甲组抽调了甲组1/4的组员。此后甲组任务也有所加重,于是又从乙组调回了重组后乙组人数的1/10。此时甲组与乙组人数相等。由此可以得出结论_____。
A: 甲组原有16人,乙组原有11人B: 甲、乙两组原组员人数之比为16∶11C: 甲组原有11人,乙组原有16人D: 甲、乙两组原组员人数之比为11∶16
参考答案: B 本题解释:[解析]正确答案为B。[解析]正确答案为B。设甲组原有a人,乙组原有b人,故由题意可得:(b+a4)×910=110(b+a4)+34a,所以
A:b=16:11。
68、某制衣厂接受一批服装订货任务,按计划天数进行生产,如果每天平均生产20套服装,就比订货任务少生产100套;如果每天生产23套服装,就可超过订货任务20套。那么,这批服装的订货任务是多少套?_____
A: 760B: 1120C: 900D: 850
参考答案: C 本题解释:参考答案:C题目详解:则由题意,设原计划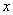 天完成,订货任务是
天完成,订货任务是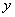 套;列方程可得:
套;列方程可得: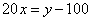
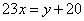 解之,得
解之,得
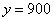 ;所以,选C。考查点:数量关系>数学运算>盈亏问题
;所以,选C。考查点:数量关系>数学运算>盈亏问题
69、马尾“胜利”号货轮在3天内共航行了150海里,请问货轮平均每天约航行多少千米?_____
A: 92.6千米B: 78.4千米C: 120.6千米D: 140.5千米
参考答案: A 本题解释:正确答案是A考点行程问题解析本题应注意单位的换算,1海里=1.852千米,由题意知货船平均每天航行1.852×150÷3=92.6千米。故正确答案为A。
70、小张的手表和闹钟走时都不准,手表比标准时间每9小时快3分钟,闹钟比标准时间每6小时慢5分钟。一天,小张发现手表指示9点27分钟,闹钟刚好指示9点41分,那么至少要经过_____小时,手表和闹钟才能指示同一时刻。
A: 6B: 9C: 12D: 15
参考答案: C 本题解释:正确答案是C考点钟表问题解析
71、大学的小李和b大学的小孙分别从自己学校同时出发,不断往返于a、b两校之间。现已知小李的速度为85米/分钟,小孙的速度为105米/分钟,且经过12分钟后两人第二次相遇。问a、b两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:正确答案是D考点行程问题解析两人第二次相遇时,两人共走的路程为a、b间距离的3倍,因此a、b两校相距(85+105)×12÷3=190×4=760米。标签尾数法
72、有甲、乙两只盒子,甲盒装有2个黑球、4个红球,乙盒装有4个黑球、3个红球,若从甲、乙两盒中各任取两球交换后,甲盒中恰有4个红球的概率为多少?_____
A:  B:
B: 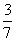 C:
C: 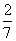 D:
D: 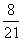
参考答案: D 本题解释:参考答案 题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有
题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有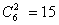 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有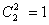 种,“1黑1红”的情形有
种,“1黑1红”的情形有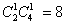 种,“2红”的情形有
种,“2红”的情形有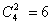 种;乙盒任取两个球:有
种;乙盒任取两个球:有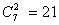 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有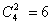 种,“1黑1红”的情形有
种,“1黑1红”的情形有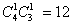 种,“2红”的情形有
种,“2红”的情形有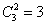 种。所以,“2黑”交换:
种。所以,“2黑”交换: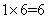 种;“1黑1红”交换:
种;“1黑1红”交换: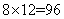 种;“2红”交换:
种;“2红”交换: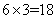 种;因此,甲盒中恰有4个红球的概率是:
种;因此,甲盒中恰有4个红球的概率是: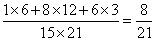 ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
73、一次数学考试共有20道题,规定:答对一题得2分,答错一题扣1分,未答的题不计分。考试结束后,小明共得23分,他想知道自己做错了几道题,但只记得未答的题的数目是个偶数。请你帮助小明计算一下,他答错了多少道题_____
A: 3B: 4C: 5D: 6
参考答案: A 本题解释:【答案】A,代入即可,答对13道题,得26分,打错3道扣3分,未答的题的数目是4道恰好是个偶数。
74、把一根钢管锯成5段需要8分钟,如果把同样的钢管锯成20段需要多少分钟?_____
A: 32分钟B: 38分钟C: 40分钟D: 152分钟
参考答案: B 本题解释:正确答案是B考点计数模型问题解析锯成5段需要锯4次,即每次需要2分钟,而锯20段需要锯19次,因此需要:19×2=38分钟,故正确答案为B。
75、一根木杆,第一次截去了全长的1/2,第二次截去所剩木杆的1/3,第三次截去所剩木杆的1/4,第四次截去所剩木杆的1/5,这时量得所剩木杆长为6厘米。问:木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:C解析:6÷(1-1/5)÷(1-1/4)÷(1-1/3)÷(1-1/2)=6÷(4/5×3/4×2/3×1/2)=6÷1/5=30(厘米)故本题选C。
76、 _____
_____
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点计算问题解析 故正确答案为C。
故正确答案为C。
77、3×999+8×99+4×9+8+7的值是_____。
A: 3840B: 3855C: 3866D: 3877
参考答案: A 本题解释:正确答案是A考点计算问题解析由于各选项尾数均不相同,故可用尾数法确定正确答案。原式各项尾数之和为7+2+6+8+7,其计算值尾数为0,故原式计算值尾数亦为0。各选项中仅3840符合,于是正确答案为A。标签尾数法
78、已知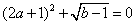 ,则
,则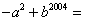 _____
_____
A: 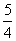 B:
B:  C:
C: 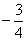 D:
D: 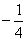
参考答案: B 本题解释:参考答案:B题目详解:由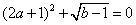 可知:
可知: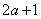 =0,
=0, =0,即
=0,即 ,
,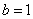 ;则原式=
;则原式=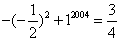 所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
79、某乐队举办一场演唱会的收入是7000元,乐队的主唱分得其中的25%,另外5名成员平分余下的收入,那么他们每人分得多少元?_____
A: 1750B: 1400C: 1120D: 1050
参考答案: D 本题解释:【答案】D。解析:主唱分25%,其余5人分75%,所以每人分15%,所以7000×l5%=1050元。
80、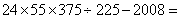 _____
_____
A: 168B: 172C: 184D: 192
参考答案: D 本题解释:参考答案 题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
81、试求出下边图形中阴影部分的面积_____。
A: 3B: 2C: 1.5D: 11
参考答案: B 本题解释:【答案】B。解析:图形正中间的正方形边长为2,那么它的面积为4。阴影面积为它的一半,所以是2。
82、一个工厂有若干个车间,为了调查产品的质量情况,采用简单随机抽样的方法,从全厂某天生产的3630件产品中抽取150件产品作样本进行质量检查。若第一车间这一天生产了440件产品,那么从该车间抽取的产品件数为_____。
A: 16B: 18C: 27D: 32
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析
83、2007年4月20日,上证综指早盘高开11点,以3460.90点开盘后,随即逐波上扬,至终盘报收于3584.20点,较上一个交易日上涨了_____
A: 3.56% B: 11点 C: 113.70点 D: 134.30点
参考答案: D 本题解释: 【解析】较上一个交易日上涨多少应该以上个交易日收盘点数为准,所以高开的11点依然属于今天上涨的部分,故有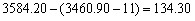 点。故选D。
点。故选D。
84、两根同样长的蜡烛,点完粗蜡烛要3小时,点完细蜡烛要1小时。同时点燃两根蜡烛,一段时间后,同时熄灭,发现粗蜡烛的长度是细蜡烛的3倍。问两根蜡烛燃烧了多长时间?_____
A: 30分钟B: 35分钟C: 40分钟D: 45分钟
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析
85、如果5*2=5+6=11,6*3=6+7+8=21,那么1*9+2*9+3*9+…+9*9=_____。
A: 629B: 729C: 759D: 829
参考答案: B 本题解释:参考答案:B题目详解:根据题意,可知:5*2表示从5开始两个自然数相加;6*3表示从6开始的三个自然数相加;那么1*9=1+2+3+4+5+6+7+8+9,2*9=2+3+4+5+6+7+8+9+10,…9*9=9+10+11+12+13+14+15+16+17;分析,可知:1*9,2*9,…,9*9每组均有9个数字相加,且后面每一组里的9个数字均比前一组里的9个数字大1,即1*9,2*9,…,9*9构成公差为9,首项为1*9=1+2+…+9=45,项数为9的等差数列;故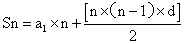 ,l*9+2*9+3*9+…+9*9=9×45+(9×8)×9÷2=729。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
,l*9+2*9+3*9+…+9*9=9×45+(9×8)×9÷2=729。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
86、科学家对平海岛屿进行调查,他们先捕获30只麻雀进行标记,后放飞,再捕捉50只,其中有标记的有10只,则这一岛屿上的麻雀大约有多少只?_____
A: 150只B: 300只C: 500只D: 1 500只
参考答案: A
87、将60拆成10个质数之和,要求最大的质数尽可能小,那么其中最大的质数是_____。
A: 5B: 9C: 7D: 11
参考答案: C 本题解释:参考答案:C题目详解:依题意:最大的质数必大于5,否则10个质数之和将不大于60;又因为60分解质因数为:60=7+7+7+7+7+7+7+2+2:故其中最大的质数为7;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>质合性
88、小张、小王二人同时从甲地出发,驾车匀速在甲乙两地之间往返行驶。小张的车速比小王快,两人出发后第一次和第二次相遇都在同一地点,那么小张的车速是小王的_____倍。
A: 1.5B: 2C: 2.5D: 3
参考答案: B 本题解释:【解析】B。行程问题。采用比例法。由题意,两人从同地出发,则第一次相遇时两人的路程和为2个全程,设其中小张走了x,小王走了y;第二次相遇 时两人走了4个全长,小张走了2y,小王走了x-y;由比例法x÷y=2y÷(x-y),解得x=2y,故两人速度比为2:1。
89、小雨把平时节省下来的全部1角的硬币先围成一个正三角形,正好用完,后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小雨所有的1角硬币合起来总共是多少钱?_____
A: 3元B: 5元C: 4元D: 6元
参考答案: D 本题解释:正确答案是D考点计数模型问题解析解析1:由硬币可围成正三角形、正方形可知,硬币总数既是3的倍数又是4的倍数,即3、4的最小公倍数是12,结合选项只有6元(即60角)满足条件,故正确答案为D。解析2:设正方形每边个数为x,则三角形每边个数为x+5,因此有4(x-1)=3(x+5-1),解得x=16。因此硬币总个数为4×(16-1)=60,也即硬币合计6元。故正确答案为D。标签最小公倍数数字特性
90、小张和小王同时骑摩托车从A地向B地出发,小张的车速是每小时40公里,小王的车速是每小时48公里。小王到达B地后立即向回返,又骑了15分钟后与小张相遇。那么A地与B地之间的距离是多少公里?_____
A: 144B: 136C: 132D: 128
参考答案: C 本题解释:C。
91、张先生向商店订购某种商品80件,每件定价100元。张先生向商店经理说:“如果你肯减价,每件减1元,我就多订购四件。”商店经理算了一下,如果减价5%,由于张先生多订购,仍可得与原来一样多的利润。则这种商品每件的成本是_____。
A: 75元B: 80元C: 85元D: 90元
参考答案: A 本题解释:正确答案是A考点经济利润问题解析设该商品每件成本x元,则未减价前每件利润为(100-x)元,减价5%后每件利润为(95-x)元,订购数量为(80+5×4)件,根据题意有80×(100-x)=(95-x)×(80+5×4),解得x=75,故正确答案为A。
92、某俱乐部会下中国象棋的有85人,会下围棋的有78人,两种都会下的有35人,两种都不会下的有18人,那么该俱乐部共有多少人?_____
A: 128B: 146C: 158D: 166
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析这是一个两集合容斥原理问题,由两集合容斥原理推论公式可知,俱乐部总人数为85+78-35+18=146(人),故正确答案为B选项。注:两集合容斥原理推论公式,满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。
93、一个长方体形状的盒子长、宽、高分别为20厘米、8厘米和2厘米,现在要用一张纸将其六个面完全包裹起来,要求从纸上剪下的部分不得用作贴补,请问这张纸的大小可能是下列哪一个?_____
A: 长25厘米,宽17厘米B: 长26厘米,宽14厘米C: 长24厘米,宽21厘米D: 长24厘米,宽14厘米
参考答案: C 本题解释:正确答案是C考点几何问题解析由题意知,盒子的表面为:2×(20×8+20×2+2×8)=432(平方厘米),纸的面积必须比盒子的表面积大才能完全包裹盒子。计算四个选项中长和宽相乘产生的面积值,A项为25×17=425(平方厘米),B项为26×14=364(平方厘米),C项为24×21>480>432(平方厘米),D项为24×14<26×14=364(平方厘米),仅C项的面积值大于432。故正确答案为C。
94、甲从某地匀速出发,一段时间后,乙从同一地点以同样的速度同向前进,在K时刻乙距离起点30米,当乙走到甲在K时刻的位置时,甲离起点108米,问,此时乙距起点多少米?_____
A: 39B: 69C: 78D: 138
参考答案: B 本题解释:正确答案:B解析:本题属于路程问题。K时刻之后,甲、乙走过的距离相等。若K时刻后,乙走过的距离为X,则2X+30=108解得X=39。此时乙和起点的距离为:30+39=69米。本题画线段图,可直接解出。故答案为B。
95、有300名求职者参加高端人才专场招聘会,其中软件设计类、市场营销类、财务管理类和人力资源类分别有100、80、70、50人,问至少有多少人找到工作才能保证一定有70名找到工作的人专业相同? _____
A: 71 B: 119 C: 258 D: 277
参考答案: C 本题解释:【答案】C 【解析】最差的情况:软件设计类、市场营销类、财务管理类和人力资源类找到工作的人数分别为69人、69人、69人、50人。此时再有任意1人即可保证一定有70名找到工作的人专业相同,即至少有69+69+69+50+1=258人。
96、某月刊杂志,定价2.5元,劳资处一些人订全年,其余人订半年,共需510元,如果订全年的改订半年,订半年的改订全年,共需300元,劳资处共多少人?_____
A: 20B: 19C: 18 D: 17
参考答案: C 本题解释: 【解析】本题用解方程的方法也可以解答,但是速度较慢。由题意可知,如果劳资处所有人都订一年半的话,总计810元;而单人订一年半的月刊需元;所以共有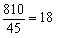 人。故选C。
人。故选C。
97、现有21朵鲜花分给5人,若每个人分得的鲜花数各不相同,则分得鲜花最多的人至少分得_____朵鲜花。
A: 7B: 8C: 9D: 10
参考答案: A 本题解释:正确答案是A考点多位数问题解析要使分得最多花的人分到的花尽可能的少,那么其他人分到的花尽可能的多。5人分到的花应尽量接近,以保证分得最多花的人分到的花尽可能少,所以最好是5个连续的自然数,21÷5=4.2,所以5人先分花数为2、3、4、5、6。2+3+4+5+6=20,还剩1朵花未分出。剩下的1朵花只能分给之前分到6朵花的人。则分得最多的人至少分得7朵鲜花,正确答案为A。
98、2009年6月17日是星期三,那么2031年6月17日是_____。
A: 星期一B: 星期二C: 星期三D: 星期四
参考答案: B 本题解释:参考答案:B题目详解:依题意:2009~2031共有22年;每个平年365天,有52个星期加1天:故每过一个平年星期+1,过了22年即星期数要加22;中间有2012、2016、2020、2024、2028。5个闰年:有2月29日,总共记“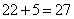 ”;
”;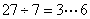 ;所以,星期三之后六天是星期二;所以,选B。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
;所以,星期三之后六天是星期二;所以,选B。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
99、甲容器有浓度为3%的盐水190克,乙容器中有浓度为9%的盐水若干克,从乙取出210克盐水倒入甲,甲容器中的盐水的浓度是多少? _____
A: 5.45%B: 6.15%C: 7.35%D: 5.95%
参考答案: B 本题解释: B。根据两溶液混合公式可得,3%×190+9%×210=(190+210)×C,解得C=6.15%。故正确答案为B。
100、小红把平时节省下来的全部五分硬币先围成一个正三角形,正好用完,后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小红所有五分硬币的总价值是_____。
A: 1元B: 2元C: 3元D: 4元
参考答案: C 本题解释:C。【解析】设三角形每条边X,正方形为Y,那么Y=X-5,同时由于硬币个数相同,那么3X=4Y,如此可以算出X=20,则硬币共有3×20=60个,硬币为5分硬币,那么总价值是5×60=300(分),得出结果。