微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、(2005北京社招,第13题)某剧院有25排座位,后一排比前一排多2个座位,最后一排有70个座位。这个剧院共有多少个座位?_____
A: 1104B: 1150C: 1170D: 1280
参考答案: B 本题解释:参考答案:B题目详解:解法一:根据项数公式: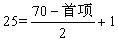 得首项=22。根据求和公式:
得首项=22。根据求和公式: 选择B。[注释]因为剧院一共有25排座位,所以座位总数肯定是25的倍数,马上得出答案为B。解法二:第一排有
选择B。[注释]因为剧院一共有25排座位,所以座位总数肯定是25的倍数,马上得出答案为B。解法二:第一排有 个座位所以总座位数是
个座位所以总座位数是 个考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
个考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
2、(2009山东,第120题)先分多次用等量清水去冲洗一件衣服,每次均可冲洗掉上次所残留污垢的四分之三,则至少需要多少次才可使得最终残留的污垢不超过初始污垢的 ?_____
?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:参考答案:B题目详解:解法一:每次清洗之后变为原来的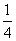 ,那么
,那么 次之后就应该是原来的
次之后就应该是原来的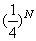 ,由题意:
,由题意: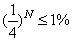 ,即
,即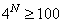 ,易知
,易知 。解法二:第一次冲洗冲洗掉
。解法二:第一次冲洗冲洗掉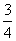 ,原污垢剩下
,原污垢剩下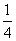 第二次冲洗原污垢的
第二次冲洗原污垢的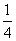 又被洗去了
又被洗去了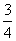 ,剩下
,剩下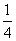 的
的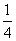 ,即
,即 以此类推第三次
以此类推第三次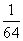 第四次冲洗,所剩下污垢就小于百分之一了。选B考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
第四次冲洗,所剩下污垢就小于百分之一了。选B考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
3、(2009河北选调,第51题)某种细菌在培养过程中,每l0分钟分裂一次(1个分裂为2个)。经过90分钟,这种细菌由1个可分裂成多少个?_____
A: 256B: 512C: 1024D: 2048
参考答案: B 本题解释:参考答案:B题目详解:周期数为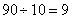 (个)。根据公式:可分裂成
(个)。根据公式:可分裂成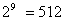 (个)。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
(个)。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
4、已知公差为2的正整数等差数列为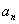 ,则该数列满足不等式
,则该数列满足不等式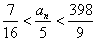 的所有项的和为:_____
的所有项的和为:_____
A: 12320B: 12430C: 12432D: 12543
参考答案: A 本题解释:参考答案:A题目详解:[解析]根据题意,公差为2的正整数数列为奇数列,将数列表示为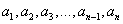 ,在数列中截取一段
,在数列中截取一段 ,因为
,因为 ,所以满足条件的最小项
,所以满足条件的最小项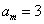 为3,最大项为
为3,最大项为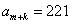 ,则根据等差数列的通项公式可知,项数为:
,则根据等差数列的通项公式可知,项数为: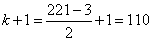 ,所有项的和为:
,所有项的和为: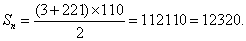 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
5、在5和29之间插入3个数字,构成5个数字的等差数列,请问离5最近的那个数为多少?_____
A: 10B: 11C: 12D: 13
参考答案: B 本题解释:参考答案:B题目详解:[解-]平均分段法:5与29相隔24,平均分成了4个6,可得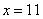 、
、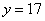 、
、 。
。 [解二]如图:
[解二]如图: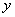 是5和29的平均数,
是5和29的平均数,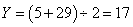 ;
; 是5和
是5和 的平均数,
的平均数, 。解法二[解一]平均分段法:5与29相隔24,平均分成了4个6,可得
。解法二[解一]平均分段法:5与29相隔24,平均分成了4个6,可得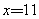 、
、 、
、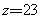 。[解二]如图:
。[解二]如图: 是5和29的平均数,
是5和29的平均数,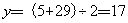 ;
; 是5和
是5和 的平均数,
的平均数, 。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等差数列第N项
。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等差数列第N项
6、(2008陕西,第13题)一根竹笋从发芽到长大,如果每天长一倍,经过10天长到40分米,那么长到2.5分米时,要经过多少天?_____
A: 6B: 8C: 4D: 12
参考答案: A 本题解释:参考答案:A题目详解:设竹笋原长A,N天长到2.5分米,则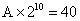 ,
,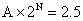 ,得N=6。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
,得N=6。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等比数列第N项
7、(2006江苏,第9题) 的值为_____。
的值为_____。
A:  B:
B: 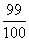 C:
C:  D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:可以化成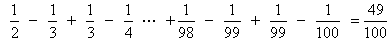 (该解析由用户“asdsds”于2010-08-2018:52:08贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
(该解析由用户“asdsds”于2010-08-2018:52:08贡献,感谢感谢!)考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
8、10个连续偶数的和是以1开始的10个连续奇数和的2.5倍,其中最大的偶数是多少?_____
A: 34B: 38C: 40D: 42
参考答案: A 本题解释:参考答案:A题目详解:[解析]根据题意,可知:以1开始的10个连续奇数和为: =100;那么,10个连续偶数的和为100×2.5=250,设最大的偶数是x,根据等差数列求和公式,则:
=100;那么,10个连续偶数的和为100×2.5=250,设最大的偶数是x,根据等差数列求和公式,则: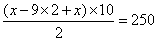 ,解得x=34。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
,解得x=34。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
9、计算的值为 _____。
_____。
A:  B:
B:  C:
C:  D:
D: 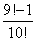
参考答案: C 本题解释:参考答案:C题目详解:观察式子用裂项法求解。原式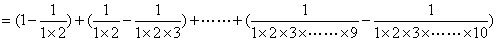

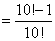 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
10、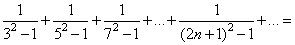 _____
_____
A: 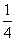 B: 1C:
B: 1C: 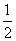 D: 无法计算
D: 无法计算
参考答案: A 本题解释:参考答案:A题目详解:前n项和为: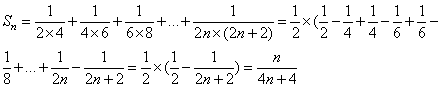 故其极限为
故其极限为 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
11、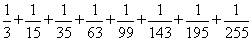 的值是_____
的值是_____
A: 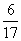 B:
B: 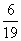 C:
C: 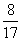 D:
D: 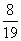
参考答案: C 本题解释:参考答案:C题目详解:本题可以拆项化简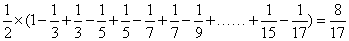 ,选择C。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
,选择C。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
12、甲乙两人从相距1350米的地方,以相同的速度相对行走,两人在出发点分别放下1个标志物。再前进10米后放下3个标志物。前进10米放下5个标志物,再前进10米放下7个标志物,以此类推。当两个相遇时,一共放下了几个标志物?_____
A: 4489B: 4624C: 8978D: 9248
参考答案: D 本题解释:参考答案 题目详解:解法一:
题目详解:解法一: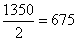 ,相遇时每人走了675米,就是每人有67个10米放下球,原点第1个球为第1项,第一个10米就是第二项,总共68项
,相遇时每人走了675米,就是每人有67个10米放下球,原点第1个球为第1项,第一个10米就是第二项,总共68项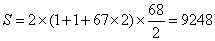 解法二:相遇时每人行走了675米,最后一次放标志物是在第670米处,放了
解法二:相遇时每人行走了675米,最后一次放标志物是在第670米处,放了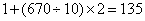 个,所有标志物个数是
个,所有标志物个数是 。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
13、(2007北京应届,第13题)某车间从3月2日开始每天调入一人,已知每人每天生产1件产品,该车间从3月1日至3月21日共生产840件产品,该车间原有工人多少名?_____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:参考答案:B题目详解:设车间原有工人n名,则人数应该是一个公差为1的等差数列。根据项数公式: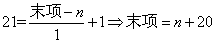 ,根据求和公式:
,根据求和公式: 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
14、小刚家住的那条街的门牌号是从1开始挨着编下去的,除小刚家外,其余各家门牌号加起来恰好等于12000。问小刚家的门牌号是多少?_____
A: 40B: 90C: 100D: 155
参考答案: B 本题解释:参考答案:B题目详解:利用逐步逼进法,可得最后一家门牌号是155。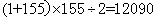 ,所以小刚家的门牌号正好是90号。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
,所以小刚家的门牌号正好是90号。考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
15、一张考试卷共有10道题,后面的每一道题的分值都比其前面一道题多2如果这张考卷的满分为100分,那么第八道题的分值应为多少分?_____
A: 9B: 14C: 15D: 16
参考答案: C 本题解释:参考答案:C题目详解:解法一:利用等差中项来解题,那么 ,所以第五道等于9分,第六道等于11分,所以第八道题是15分。解法二:这是一道等差数列的应用题,其^91考试网差为2,数列之和为100,总共十个项.根据公式
,所以第五道等于9分,第六道等于11分,所以第八道题是15分。解法二:这是一道等差数列的应用题,其^91考试网差为2,数列之和为100,总共十个项.根据公式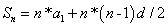 其中
其中 已知为100,
已知为100, 已知为10,
已知为10,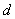 已知为2.所以可以求得
已知为2.所以可以求得 ,题目问的是
,题目问的是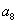 .根据公式
.根据公式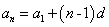 .则
.则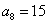 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等差数列第N项
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>求第N项>等差数列第N项