1、从12时到13时，钟的时针与分针可成直角的机会有_____。
A: 1次B: 2次C: 3次D: 4次
参考答案: B 本题解释:【答案解析】一个小时内成直角只有两次，选B。

2、马场有甲、乙、丙、丁四个入口可以提供人进入游玩，如果现在开了甲、乙两个入口，经过了4．5小时游客全部能够进入，如果开乙、丙两个入口，游客3小时能全部进入，如果开丙、丁两个入口，游客3．5小时全部进入。若只打开甲、丁两个入口，则需要几个小时，游客才能全部进入？_____
A: 63/11B: 63/32C: 196/33D: 172/33
参考答案: A 本题解释:【答案】A。解析：设总人数为1，则开甲、乙两个口，1小时能进入2/9人；开乙、丙两个口，1小时能进入1/3人；开丙、丁两个口，一小时能进入2/7人；三种情况同时存在时，一小时能进入的人数为甲口+乙口+乙口+丙口+丙口+丁口=2（乙口+丙口）+甲口+丁口=2/9+1/3+2/7＝53/63（人）。又因乙口+丙口=1/3（人），所以甲、丁两口同时开放，1小时进入的人数为11/63人。所以只打开甲、丁两个口，游客全部进入，需要的时间是63/11小时。

3、把1～200这200个自然数中，既不是3的倍数，又不是5的倍数，从小到大排成一排，那么第100个是几?_____
A: 193B: 187C: 123D: 40
参考答案: B 本题解释:B【解析】 从1至200的自然数中是3的倍数的数有66个，是5的倍数的数有40个，而既是3又是5的倍数的数有13个。所以从1至200的自然数中是3或5的倍数的数有（66+40-13）=93个，所以从1至200的这200个自然数中，既不是3又不是5的倍数的数有（200-93）=107个。现在要求第100个，即倒数第8个。将它从大到小列出：199、197、196、194、193、191、188、187……即从小到大排列第100个是187。故本题选B。

4、一个班有50名学生，他们的名字都是由2个或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5B: 8C: 10D: 12
参考答案: C 本题解释:【解析】C。不定方程问题。由题意两组学生名字字数相差10，两边人数相同，即其中一组比另一组三名字人数多10人，则2名字人数少10人。

5、一条公路旁有A、B、C、D、E5个货站。每两个货站之间的距离相等，现要将这5个货站集中到一个货站，已知A、B、C、D、E的货物分别为70吨、30吨、60吨、50吨、40吨，问应集中到哪一个货站可使运费最省? _____
A: AB: BC: CD: E
参考答案: C 本题解释:C。五个货站物资总数的一半为（70+30+60+50+40）÷2=125吨，因为A、E两站都小于125吨，所以都往中间靠一站，此时，B站：30+70=100吨，D站：50+40=90吨，B、D两站仍小于125吨，再往中间靠一站，集中到C站。因此集中到C站可使运费最省。

6、加油站有150吨汽油和102吨柴油，每天销售12吨汽油和7吨柴油。问多少天后，剩下的柴油是剩下的汽油的3倍？_____
A: 9B: 10C: 11D: 12
参考答案: D 本题解释:【答案】D。解析：假设x天，汽油还剩150-12x，柴油还剩102-7x，102-7x=3（150-12x），解得x=12，答案为D。

7、把黑桃、红桃、方片、梅花四种花色的扑克牌按黑桃10张、红桃9张、方片7张、梅花5张的顺序循环排列。问第2015张扑克牌是什么花色？_____
A: 黑桃 B: 红桃 C: 梅花 D: 方片
参考答案: C 本题解释:【答案】C。解析：一个完整的循环包括黑桃10张，红桃9张，方片7张，梅花5张，共31张，2015÷31=65，刚好可以被31整除，因此第2015张牌是梅花。正确答案为C。

8、某次投资活动在三个箱子中均放有红、黄、绿、蓝、紫、橙、白、黑8种颜色的球各一个，奖励规则如下：从三个箱子中分别摸出一个球，摸出的3个球均 为红球的得一等奖，摸出的3个球中至少有一个绿球的得二等奖，摸出的3个球均为彩色球(黑.白除外)的得三等奖。那么不中奖的概念是_____。
A: 在0-25%之间B: 在25-50%之间C: 在50-75%之间 D: 在75-100%之间
参考答案: C 本题解释:【解析】C。概率问题。中奖概率为（3/4）3+C13×（1/8）×（1/4）2+C23×（1/8）2×（1/4）=117÷256＜50%，故不中奖的概率略大于50%。

9、有两种溶液，甲溶液中蛋清的浓度为20%，蜂蜜的浓度为15%，乙溶液中蛋清的浓度为50%，蜂蜜的浓度为20%，现在有甲溶液2千克，要将一定量的乙溶液与甲溶液混合，混合后所得溶液的蛋清浓度是蜂蜜浓度的2倍，问需要多少千克的乙溶液？_____
A: 2B: 1.5C: 1D: 0.5
参考答案: A 本题解释:A。

10、甲、乙、丙、丁四人步行，在同时间内甲行5步时乙可行6步;乙行7步时丙可行8步;丙行9步时丁可行10步。又甲、乙、丙、丁每步的距离之比为15∶14∶12∶10。问甲行630米时，丁可行多少米?_____
A: 640米B: 680米C: 720米D: 750米
参考答案: A 本题解释:A【解析】将四人步数之比与每步距离之比结合考虑，可推出相同时间内两人所行距离之比，并由此求出丁所行的步数。即甲∶乙=（15×5）∶（14×6）=25∶28，乙∶丙=（14×7）∶（12×8）=49∶48，丙∶丁=（12×9）∶（10×10）=27∶25。可得甲行630米时丁行（28×48×25×630）÷（25×49×27）=640米。故甲行630米时丁行640米。

11、某市财政局下设若干处室，在局机关中不是宣传处的有206人，不是会计处的有177人，已知宣传处与会计处共有41人，问该市财政局共有多少人？_____
A: 218 B: 247 C: 198 D: 212
参考答案: D 本题解释: 【解析】由题意有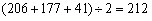：人。所以选D。

12、用数字0，1，2(既可全用也可不全用)组成的非零自然数，按从小到大排列，问“1010”排在第几个?_____
A: 30B: 31C: 32D: 33
参考答案: A 本题解释:本题实际求由0，1，2构成的数字中，小于1010的有多少个。位数不固定，先按位数分类，再对每类进行计数。显然组成的非零一位数有2个;两位数有2×3=6（个）;三位数有2×3×3=18（个）;四位数中比1010小的为1000，1001，1002共计3个。故1010排在第30位。故选A。

13、某工厂11月份工作忙，星期六、日不休息，而且从第一天开始，每天下班后都从总厂陆续派相同人数的工人到分厂工作，直到月底下班后，总厂还剩工人238人。如果月底统计总厂工人的工作量是8070个工作日(1人工作1天为1个工作日)，且无1个缺勤，那么，这个月由总厂派到分厂工作的工人共多少人？_____
A: 46人B: 30人C: 60人D: 62人
参考答案: C 本题解释:11月份有30天。设每天下班后派往分厂的人数为2，则根据题意可知，最后一天总厂的工作量为238+z，可列方程238+x+238+2x+…+238+30x=8070，解得x=2，即每天派2人到分厂工作，11月份30天共派了60人到分厂。故答案为C。

14、假定一对刚出生的小兔一个月能长成大兔，再过一个月便能生下一对小兔，并且此后每个月都生一对小兔。如果一切正常没有死亡，公母兔也比例适调，那么一对刚出生的兔子，一年可以繁殖成_____对兔子。
A: 144B: 233C: 288D: 466
参考答案: A 本题解释:【答案】A。解析：先列举出经过一到六个月兔子的对数分别是1、1、2、3、5、8。很容易发现这个数列的特点：即从第三项起，每一项都等于前两项之和。按这个规律写下去，便可得出一年内兔子繁殖的对数：1、1、2、3、5、8、13、21、34、55、89、144。可见一年内兔子共有144对。故正确答案为A。

15、某中介服务机构根据服务项目所涉及的金额分段按一定比例收取服务费，具体标准如下：1万元(含)以下收取50元；1万元以上、5万元(含)以下的部分收取3%；5万元以上、10万元(含)以下的部分收取2%.(如某一服务项目所涉及金额为5万元时，应收取服务费1250元。)现有一服务项目所涉及金额为10万元，那么，所收取的服务费应为：_____
A: 2250元 B: 2500元 C: 2750元 D3000元
参考答案: A 本题解释:【解析】分段按比例计算，选A.

16、小明前三次数学测验的平均分数是88分，要想平均分数达到90分以上，他第四次测验至少要达到_____
A: 98分B: 96分C: 94分D: 92分
参考答案: B 本题解释: 【解析】B。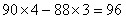分，该数值可以根据以上式子判定尾数为6，选择B。

17、有7个不同的质数,他们的和是58,其中最小的质数是多少?_____。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:【答案】A。解析:除了2以外的质数全是奇数,如果7个数全是奇数的话,他们的和不会是58这个偶数,所以,7个数中必然有2,而2是所有质数中最小的一个。(2、3、5、7、11、13,17这7个质数的和为58)

18、小红把平时节省下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是_____。
A: 1元B: 2元C: 3元D: 4元
参考答案: C 本题解释:C。【解析】设三角形每条边X，正方形为Y，那么Y=X-5，同时由于硬币个数相同，那么3X=4Y，如此可以算出X=20，则硬币共有3×20=60个，硬币为5分硬币，那么总价值是5×60=300（分），得出结果。

19、2010年5月1日世博会开幕，当天是星期六，则2007年3月1日是_____。
A: 星期一B: 星期二C: 星期三D: 星期四
参考答案: D 本题解释:D【解析】由题意2010年5月1日星期六，则与2007年5月1日月份日期相同，根据核心口诀︰①一年就是1——从2007年至2010年是三年，所以加“3”②闰月再加1——从2007年至2010年1个闰月，所以加“1”又由于2007年3月1日至5月1日中间相隔2个月，所以就是“4”，多少再补算——3月31日一个“31”日，加1，故应在2010年5月1日星期六基础上减3+1+4+1=9天，最后可得2007年3月1日是星期四，正确答案为D选项。

20、某单位《普法知识问答》的总平均分为87分，男同志的平均分为85分，女同志的平均分为90分，问此单位的男、女比例是多少？_____
A: 2/3B: 3/4 C: 3/2 D: 4/3
参考答案: C 本题解释:C。设女同志为1，男同志为 ，则（85x+90）÷（1+x）=87，解得x=3/2，即为男、女的比例，选C。

21、某公交线路有15站，假设一辆公交车从起点站出发，从起点站后，每一站都会有到前方每一站下车的乘客各一名上车，那么在第九站和第十站之间，车上有_____人？
A: 48B: 54C: 56D: 60
参考答案: B 本题解释:【答案】B。解析：解析1：总站点数为M，求第N站和第N＋1之间车上的人数，有下述公式，车上的人数＝N×（M－N），可知所求人数为9×（15-9）＝9×6＝54，故选B。解析2：第一站点有14个人上车，没有人下车，第二个站点有13个人上，1个人下车，所以到第九站时候，前面上车人数为14，13，12，11，10，9，8，7，6，根据等差数列求和公式，一共有（14＋6）×9÷2=90人，下车的人数为1，2，3，4，5，6，7，8，一共有（1＋8）×8÷2＝36，则到第九站点后，车上人数等于一到第九站上车的人减去一到第九站下车的人数，即90-36=54，故选B选项。此题不用考虑过于复杂，起始站为第一站。

22、除以5余1，b除以5余4，如果3a >b，那么3a-b除以5余几? _____
A: 1B: 2C: 3D: 4
参考答案: D 本题解释:D【解析】3a 除以5 应余1×3=3，已知b 除以5 余4，则3a-b 除以5 余3-4+5=4。故选D。

23、把若干个大小相同的水立方摆成如图形状！从上向下数，摆1层有1个立方体，摆2层共有4个立方体，摆3层共有10个立方体，问摆7层共有多少个立方体？_____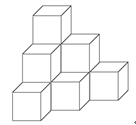
A: 60B: 64C: 80D: 84
参考答案: D 本题解释:【答案】D。解析：根据规律得出数列：1+3+6+10+15+21+28=84。

24、女儿2013年时的年龄是母亲年龄的1/4，40年后女儿的年龄是母亲年龄的2/3。问当女儿年龄是母亲年龄的1/2时是公元多少年？_____
A: 2021 B: 2022 C: 2026 D: 2029
参考答案: D 本题解释:【答案】D。

25、某服装厂生产某种定型冬装，9月份销售每件冬装的利润是出厂价的25%(每件冬装的利润=出厂价-成本)。10月份将每件冬装的出厂价调低10%，成本降低10%，销售件数比9月份增长80%，那么该厂10月份销售这种冬装的利润比9月份的利润总额增长:_____
A: 2%B: 8%C: 40.5%D: 62%
参考答案: D 本题解释:【解析】D。设出厂价为100，则9月份单件利润是25，成本为75。10月的出厂价为90，成本为75×0.9=67.5，单件利润为90-67.5=22.5。设9月的销售量为1，则10月为1.8。9月总利润为25，10月为1.8×22.5=40.5，10月比9月总利润增长40.5÷25-1=62%。

26、(101+103+…+199)-(90+92+…+188)=_____。
A: 100　B: 199　C: 550　D: 990
参考答案: C 本题解释:C[解析]提取公因式法。101-90=11，103-92=11，……，199-188=11，总计有50个这样的算式，所以50×11=550，选择C。

27、甲乙两个工厂的平均技术人员比例为45%，其中甲厂的人数比乙厂多12.5%，技术人员的人数比乙厂的多25%，非技术人员人数比乙厂多6人。甲乙两厂共有多少人_____
A: 680B: 840C: 960D: 1020
参考答案: A 本题解释:【答案】A。解析：设甲厂技术人员有x，则乙厂有9x/8，两厂共有17x/8，即两厂总人数是17的倍数，选项中只有A、D符合。代入可知A符合题意。

28、四个相邻质数之积为17 017,他们的和为_____。
A: 48B: 52C: 61D: 72
参考答案: A 本题解释:【答案】A。解析:l7017=l7×l3×11×7,它们的和为48。

29、小张数一篇文章的字数，二个二个一数最后剩一个，三个三个一数最后剩一个，四个四个一数最后剩一个，五个五个一数最后剩一个，六个六个一数最后剩一个，七个七个一数最后剩一个，则这篇文章共有多少字?_____
A: 501B: 457C: 421D: 365
参考答案: C 本题解释: 【解析】C。这道题实际只要考虑五个五个一数最后剩一个，三个三个一数最后剩一个，即可。这两个最好思考。只有501与421一幕了然，除以5余1。而501能被3整除，只有42。

30、为帮助果农解决销路，某企业年底买了一批水果，平均发给每部门若干筐之后还多了12筐，如果再买进8筐则每个部门可分得10筐，则这批水果共有_____筐。
A: 192B: 198C: 200D: 212
参考答案: A 本题解释:【答案】A。解析：总数加8应能被10整除，如果为A，则部门数为20；如果为D，部门数为22，则212÷22=9……14不符合题意。故选择A。

31、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2，而4/9和151/301都大于1/2，所以只要比较二者的大小就可以，通过计算，151/301大，所以选择D。

32、某公司招聘甲、乙两种职位的人员共90人，甲、乙两种职位人员每月的工资分别为1500元和2500元，若甲职位的工资总支出是乙职位的40%，则乙职位招聘人数比甲职位多：_____
A: 24人B: 20人C: 18人D: 15人
参考答案: C 本题解释:【答案】C。解析：设甲职位有x人，则Z乙职位有（90-x）人。依题意有l500x=2500×（90-x）×40%，x=36人。因此乙职位有90-36=54人，比甲职位多54-36=18人。快速突破甲、乙职位的人均工资之比为1500：2500=3：5;甲职位的工资总支出是乙职位的40%，则甲、乙职位的总工资支出之比为40%：1=2：5，所以甲、乙职位的招聘人位之比为2/3：5/5=2：3，甲、乙共招聘90人，则乙职位招聘人数比甲职位多90×（3-2）/（3+2）=18人。

33、甲、乙两人从400米的环形跑道的一点A背向同时出发，8分钟后两人第三次相遇。已知甲每秒钟比乙每秒钟多行0.1米，那么，两人第三次相遇的地点与A点沿跑道上的最短距离是_____
A: 166米B: 176米C: 224米D: 234米
参考答案: B 本题解释:B.【解析】400-（480×0.1）=352/2=176米。

34、某项工程，甲单独完成需要8天，乙需要4天，甲做一半换乙，乙做剩余一半又换甲，甲又做剩余一半再换乙完成。问整个工程花费_____天。
A: 5.5 B: 6 C: 6.5 D: 7
参考答案: C 本题解释:C。假设工作总量为8，则甲每天完成1，乙每天完成2，甲先完成一半需要4÷1＝4天，乙完成剩下一半需要2÷2＝1，甲又做剩余一半需要1÷1＝1天，剩下乙完成需要1÷2＝0.5天，因此共需要6.5天。

35、某次考试100道选择题，每做对一题得1.5分，不做或做错一题扣1分，小李共得100分，那么他答错多少题_____
A: 20B: 25C: 30D: 80
参考答案: A 本题解释:A【解析】不做或做错的题目为(100×1.5-100)÷(1.5+1)=20。

36、用3、9、0、1、8、5分别组成一个最大的六位数与最小的六位数，它们的差是_____。
A: 15125B: 849420C: 786780D: 881721
参考答案: D 本题解释:D最大的数为985310，最小的数为103589，故它们的差为881721。

37、A、B、C、D四支球队开展篮球比赛，每两个队之间都要比赛1场，已知A队已比赛了3场，B队已比赛了2场，C队已比赛了1场，D队已比赛了几场？（）
A: 3B: 2C: 1
参考答案: B 本题解释:每个球队要比赛3场，则A队和B队、C队、D队各比赛1场，C队和A队比赛1场，B队和A队、D队各比赛1场，故D队比赛了2场。所以选B。

38、1996+1997+1998+1999+2000+2001等于_____。
A: 11986B: 11991C: 12987D: 12989
参考答案: B 本题解释: B 【解析】原式=（2000-4）+（2000-3）+（2000-2）+（2000-1）+（2000+1）=2000×6-4-3-2+1=12000-9=11991。

39、173×173×173-162×162×162=_____。
A: 926183B: 936185C: 926187D: 926189
参考答案: D 本题解释:D【解析】利用简单的猜测法。173的尾数是3，3的立方为27;162的尾数是2，2立方为8。两者相减尾数为9，所以判断173和162的立方之差的尾数为9。所以答案为D项。

40、某商店实行促销手段，凡购买价值200元以上的商品可以优惠20％，那么用300元钱在该商店最多可买下价值_____元的商品。
A: 350元B: 384元C: 375元D: 420元
参考答案: C 本题解释:C【解析】300/80%=375元。故选C。

41、从一张1952mm×568mm的长方形纸片上，剪下一个边长尽可能大的正方形，如果剩下的部分不是正方形，那么在剩下的纸片上再剪下一个边长尽可能大的正方形。按照上面的过程不断地重复，最后一共可剪得正方形多少个？_____
A: 8B: 10C: 12D: 14
参考答案: D 本题解释:从长1952mm、宽568mm的长方形纸片上首先可剪下边长为568mm的正方形，这样的正方形的个数恰好是1952除以568所得的商，而余数恰好是剩下的长方形的宽，于是有：1952÷568=3…248，568÷248=2…72，248÷72=3…32，72÷32=2…8，32÷8=4，因此一共可得到正方形3+2+3+2+4=14（个），故正确答案为D。

42、一个三位数，各位上的数的和是15，百位上的数与个位上的数的差是5，如颠倒各位上的数的顺序，则所成的新数比原数的3倍少39。求这个三位数。_____
A: 196B: 348C: 267D: 429
参考答案: C 本题解释:【解析】C。代入法。首先排除A和D;根据所成的新数比原数的3倍少39，用每个选项的最后一个数乘以3再减去，所得的数只有C中有。

43、六位同学数学考试的平均成绩是92.5分，他们的成绩是互不相同的整数，最高分是99分，最低分是76分，则按分数从高到低居第三位的同学至少得多少分_____。
A: 93B: 94C: 95D: 96
参考答案: C 本题解释:C。本题为构造类题目。总分为92.5×6=555，去掉最高分和最低分后还有555-99-76=380。要使第三名分尽可能的低，首先第二名分要尽可能高，即为98分(还余282分)。而第四和第五名的分数要尽量的高，与第三名的分最接近，三者的分为93，94，95。那么最高分至少为95。所以选择C选项。

44、小明和小红积极参加红领巾储蓄活动，把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品，那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元？_____
A: 44B: 64C: 75D: 86
参考答案: B 本题解释:【答案】B。解析：设小明原来存了Y元，则小红存了Y＋20元，根据题意得（Y－12）×3＝（Y＋20－12），解得Y＝22元。因此两人原来共存了2Y＋20＝64元，故正确答案为B。

45、有11个人围成一个圆圈，依次编成1—11号，从1号起轮流表演节目，轮流的方法是：隔一个人表演一个节目，隔两个人表演一个节目，再隔一个人表演一个节目，隔两个人表演一个节目……这样轮流下去，至少要表演多少个节目，才能使每个人表演的次数同样?_____
A: 22B: 24C: 25D: 28
参考答案: A 本题解释:A【解析】本题考查的是周期问题。表演的人数共11人，且每个人表演次数相同，则至少要表演11N个节目。符合条件的只有A。

46、出租车队去机场接某会议的参会者，如果每车坐3名参会者，则需另外安排一辆大巴送走余下的50人;如每车坐4名参会者，则最后正好多出3辆空车。问该车队有多少辆出租车?_____
A: 50B: 55C: 60D: 62
参考答案: D 本题解释:方程问题。设有x辆出租车，由题意列方程：3x+50=4（x-3），解得x=62。

47、甲、乙两时钟都不正确，甲钟每走24小时，恰好快1分钟;乙钟每走24小时，恰好慢1分钟。假定今天下午三点钟的时候，将甲、乙两钟都调好，指在准确的时间上，任其不停地走下去，问下一次这两只钟都同样指在三点时，要隔多少天?_____
A: 30B: 240C: 480D: 720
参考答案: D 本题解释:【答案解析】可以先求出甲钟比标准时钟多转一圈所需天数，标准时钟比乙钟多走一圈所需天数，然后再求二者的最小公倍数。甲钟与标准时钟下一次同时指向三点时，甲钟比标准时钟多转一圈，也就是多走12小时，即60×12分钟，需要60×12÷(61-60)=720÷1=720(天)同样，标准时钟与乙钟下一次同时指向三点时，标准时钟比乙钟多转一圈，需要60×12÷(60-59)=720÷1=720(天)所以，经过720天后，甲、乙两钟同时指在三点。故正确答案为D。

48、一个两位数除以一个一位数，商仍是两位数，余数是8。问：被除数、除数、商以及余数之和是多少? _____
A: 98B: 107C: 114D: 125
参考答案: D 本题解释:【答案】D。解析：猜证结合的98÷10=9余8，10+98+9+8=125。

49、用1，2，3，4，5这五个数字组成没有重复数字的自然数，从小到大顺序排列：1，2，3，4，5，12，……，54321。其中，第206个数是_____
A: 313 B: 12345 C: 325 D: 371
参考答案: B 本题解释:B。由1、2、3、4、5组成的没有重复数字的一位数共有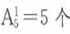；二位数共有个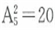；三位数共有个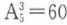；四位数共有个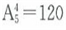；至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个；那么第206个数是第一个由1、2、3、4、5组成的五位数，即最小的五位数12345。

50、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：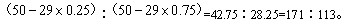

51、一艘游轮从甲港口顺水航行至乙港口需7小时，从乙港口逆水航行至甲港口需9小时。问如果在静水条件下，游轮从甲港口航行至乙港口需多少小时?_____
A: 7.75B: 7.875C: 8D: 8.25
参考答案: B 本题解释:

52、甲乙两辆汽车都由北京经长沙开往广州，出发时两车共有乘客160人，在长沙站甲车增加17人，乙车减少23人。这样在开往广州时，两车的乘客人数正好相等，请问甲车原有多少人?_____
A: 60人B: 75人C: 90人D: 100人
参考答案: A 本题解释:A【精析】两车经过长沙站后，总人数变为160+17-23=154人，这时两车人数相等，则甲车此时人数为154÷2=77人。而在长沙站甲车增加了17人，因此甲车原有77—17=60人。

53、某校下午2点整派车去某厂接劳模作报告，往返须1小时。该劳模在下午1点整就离厂步行向学校走来，途中遇到接他的车，便坐上车去学校，于下午2点40分到达。问汽车的速度是劳模的步行速度的几倍？_____
A: 4 B: 6 C: 7 D: 8
参考答案: D 本题解释:【解析】本题要画图辅助，假设全程距离为1，汽车来回的时间为1小时，所以，其速度为1，汽车运行时间为2/3小时，所以汽车跑的路程为2/3，人走的距离为剩下1/3路程的一半，即1/6，步行的时间为1小时20分，所以步行的速度是1/6÷（1+1/3）＝1/8，所以汽车的速度是劳模的8倍。选D.

54、在1至1000的1000个自然数中，既不是4的倍数，也不是6的倍数的数共有多少个?_____
A: 375B: 416C: 625D: 791
参考答案: C 本题解释:C【解析】1000÷4=250（个），所以1至1000中4的倍数的数有250个。1000÷6=166……4，所以1至1000中6的倍数的数有166个。1000÷（4×6）=41……16，说明1至1000中既是4的倍数，又是6的倍数的数有41个。即4的倍数的个数与6的倍数的个数的交集有41个，如图所示。所以1至1000中，既是4的倍数，也是6的倍数的数共有209+125+41=375（个）。则1至1000中，既不是4的倍数，也不是6的倍数的数共有：1000-（209+125+41）=1000-375=625（个）。故本题选C。

55、由1、2、3组成的没有重复数字的所有三位数之和为多少？_____
A: 1222 B: 1232 C: 1322 D: 1332
参考答案: D 本题解释:D。因为1、2、3之和可被3整除，故而1、2、3所组成的没有重复数字的三位数都能被3整除，而这些数字相加之和也必能被3整除，只有D项能被3整除，为正确答案。根据排列组合原理，可知该没有重复数字的三位数共有6个，1、2、3三个数在个、十、百位上各出现两次，即（1+2+3）×2=12，也就是说这一数字当为12+120+1200=1332。

56、一个慢钟每小时比标准时间慢5分钟，一个快钟每小时比标准时间快3分钟。如果将两个钟同时调到标准时间，在24个小时内的某个时间，慢钟显示7:50，快钟显示9:10。那么此时的标准时间应该是什么?_____
A: 8:20B: 8:30C: 8:40D: 8:50
参考答案: C 本题解释:C.【解析】这是一道快慢钟问题。快钟每小时比慢钟快8分钟，而7:50与9:10之间相差80分钟，则此时距离将两个钟调成标准时间为80÷8=10个小时，10个小时的时间，慢钟共少走了5×10=50分钟，则标准时间应该为8:40。因此，本题的正确答案为C选项。

57、甲容器有浓度为3%的盐水190克，乙容器中有浓度为9%的盐水若干克，从乙取出210克盐水倒入甲，甲容器中的盐水的浓度是多少？_____
A: 5.45%B: 6.15%C: 7.35%D: 5.95%
参考答案: B 本题解释:【答案】B。解析：根据两溶液混合公式可得，3%×190＋9%×210＝（190＋210）×C，解得C＝6.15%。故正确答案为B。

58、1.31×12.5×0.15×16的值是_____。
A: 39.3B: 40.3C: 26.2D: 26.31
参考答案: A 本题解释:A【解析】本式可写为1.31×12.5×4×0.15×4。

59、1898年4月1日，星期五，分别把三个钟调整到相同的时间：12点。第二天中午发现A钟时间完全准确，B钟正好快了1分钟，C钟正好慢了1分钟。现在假设三个钟都没有被调，它们保持着各自的速度继续走而且没有停。那么到_____，三只时钟的时针分针会再次都指向12点。
A: 1900年3月20日正午12点B: 1900年3月21日正午12点C: 1900年3月22日正午12点D: 1900年3月23日正午12点
参考答案: C 本题解释:【答案】C。解析：B钟1天时间快了1分钟，C钟1天时间慢了1分钟，若他们时针分针都再次指向12点，那么，B钟总共快了12小时，同时C钟慢了12小时。那么需要的时间为60×12＝720天，由此，此题变成1898年4月1日的720天后是几月几日的问题。由于1899年跟1900年都为平年，所以两年即730天后为1900年4月1日，往前数10天为3月22日，故正确答案为C。此题要注意闰年的计算方法：公元年数可被4整除（但不可被100整除）为闰年，但是正百的年数必须是可以被400整除的才是闰年，所以1900年是平年。

60、如下图，梯形ABCD的对角线AC⊥BD，其中AD=1/2，BC=3，AC=2×4/5，BD=2.1。问梯形ABCD的高AE的值是_____。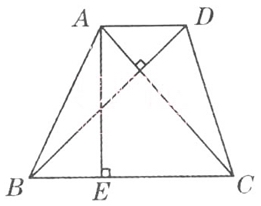
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=（AD+BC）×AE→AE=42/25。

61、某班46个同学要在A、B、C、D、E五位候选人中选出一位体育委员。已知A得选票25张，B得选票占第二位，C、D得票相同，而E选票最少，只得4票。那么B得了多少张选票?_____
A: 7张B: 9张C: 6张D: 4张
参考答案: A 本题解释:【解析】由题干可知，B、C、D三人共得选票46-25-4=17（张）。设C、D每人得票数为m，B得票数为n，则有2m+n=17（n>m），则m=5，n=7。故B得选票为7张。

62、男女并排散步，女的3步才能跟上男的2步。两人从都用右脚起步开始到两人都用左脚踏出为止，女的应走出多少步？_____
A: 6步B: 8步C: 12步D: 多少步都不可能
参考答案: D 本题解释:【解析】D。两人的出脚顺序以6步为一个循环。在这6步中，两人没有一次同时出左脚，因此多少步都不可能。

63、在一次国际美食大赛中，中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94，法国评委和日本评委给出的平均分是90，日本评委和俄国评委给出的平均分是92，那么中国评委和俄国评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C 解析：设中、法、日、俄四国的评委给出的分数分别是A、B、C、D，根据题意可知：A+B=94×2，B+C=90×2，C+D=92×2，又因为A+D=（A+B）+（C+D）-（B+C）=94×2+92×2-90×2=（94+92-90）×2=96×2所以中国评委和俄国评委给出的平均分是96分，本题正确答案为C。

64、某玩具店同时卖出一个拼装玩具和一架遥控飞机，拼装玩具66元，遥控飞机120元，拼装玩具赚了10%，而遥控飞机亏本20%，则这个商店卖出这两个玩具赚钱或是亏本多少_____
A: 赚了12元B: 赚了24元C: 亏了14元D: 亏了24元
参考答案: D 本题解释:答案：D 解析：根据题意，拼装玩具赚了66÷（1+10%）×10%=6元，遥控飞机亏本120÷（1-20%）×20%=30元，故这个商店卖出这两个玩具亏本30-6=24元。

65、一本100多页的书，被人撕掉了4张，剩下的页码总和为8037，则该书最多有多少页？_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析：撕掉一张纸，其正反两面的两个页码之和为奇数，则撕掉4张，页码总数必为偶数，剩余页码和为8037，所以原书的页码总和必然为奇数，由此排除BD（BD选项能被4整除，而连续4页的页码和必然为偶数）。代入C，可知整书的页码总和为（1＋138）÷2×138＝9591，于是撕掉的页码和为9591－8037＝1554，那么撕掉的8页的页码平均值为194.25，显然与最多138页矛盾。故正确答案为A。

66、一根木杆，第一次截去了全长的1/2，第二次截去所剩木杆的1/3，第三次截去所剩木杆的1/4，第四次截去所剩木杆的1/5，这时量得所剩木杆长为6厘米。问：木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:C解析：6÷（1-1/5）÷（1-1/4）÷（1-1/3）÷（1-1/2）=6÷（4/5×3/4×2/3×1/2）=6÷1/5=30（厘米）故本题选C。

67、一堆沙重480吨，用5辆载重相同的汽车运3次，完成了运输任务的25%，余下的沙由9辆同样的汽车来运，几次可以运完？_____
A: 4次B: 5次C: 6次D: 7次
参考答案: B 本题解释:【答案】B。解析：因为用5辆载重相同的汽车运3次，完成了运输任务的25%，所以每辆车一次可以运总工程量的（25÷5÷3）％＝（5/3）％，所以9辆车一次可以运总工程量的9×（5/3）％＝15％，余下的75％用9辆车运的话需要75÷15＝5次，故正确答案为B。

68、一个车队有三辆汽车， 担负着五家工厂的运输任务，这五家工厂分别需要 7、9、4、10、6 名装卸工，共计 36 名;如果安排一部分装卸工跟车装卸，则不需要那么多装卸工，而只需要在装卸任务较多的工厂再安排一些装卸工就能完成装卸任务。那么在这种情况下，总共至少需要_____名装卸工才能保证各厂的装卸需求?_____
A: 26　　B: 27　　C: 28　　D: 29
参考答案: A 本题解释:【答案】A[解析]要求最少，那么三辆车分别装五家工厂里面最大的三个需求量，则可以满足条件，分别装10、9、7， 所以是10+9+7=26，选A。

69、某单位有185人。在某次乒乓球比赛中。有12%的男员工和12.5%的女员工参加这次比赛。则该单位男员工有多少人？_____
A: 25B: 65C: 105D: 125
参考答案: A 本题解释:A。

70、有一种红砖，长24厘米、宽12厘米、高5厘米，问至少用多少块这种砖才能拼成一个实心的正方体?_____
A: 600块B: 1200块C: 1800块D: 2400块
参考答案: B 本题解释:B。

71、8项不同的工程由三个工程队承包，每队至少承包2项，则不同的承包方案有多少种?_____
A: 5880种B: 2940种C: 1960种D: 490种
参考答案: B 本题解释:B【解析】8项不同的工程可以分为2、2、4和2、3、3两种情况，所以共有C28C26A33÷A22+C38C35A33÷A22=2940种。

72、小木、小林、小森三人去看电影，如果用小木带的钱去买三张电影票，还差0.55元;如果用小林带的钱去买三张电影票，还差0.69元;如果用三人带去的钱买三张电影票，就多0.30元，已知小森带了0.37元，那么买一张电影票要用多少元?_____
A: 1.06B: 0.67C: 0.52D: 0.39
参考答案: D 本题解释:D【解析】设每张电影票x元，则小木的钱数为3x-0.55元，小林的钱数为3x-0.69元，小森的钱数为0.37元。三人的钱数和为3x+0.30元，即可得出：3x-0.55+3x-0.69+0.37=3x+0.30，求得x=0.39（元）。

73、有甲、乙两汽车站，从甲站到乙站与从乙站到甲站每隔10分同时各发车一辆，且都是1小时到达目的地。问某旅客乘车从甲站到乙站，在途中可看到几辆从乙站开往甲站的汽车?_____
A: 9B: 13C: 14D: 11
参考答案: D 本题解释:D 【解析】某旅客所乘之车在甲站起动时，正好有一辆从乙站开来的车到站停车;同样，当该旅客所乘之车到达乙站时，正好有一辆车从乙站开出，这两辆车均不算该旅客在“途中”看到的，这时，下一辆从乙站开来的汽车离甲站还有10分钟的路程，这辆车与该旅客所乘的车相向而行，相遇时，离甲站有10÷2=5（分钟）的路程。由此可推知，该旅客在途中每隔5分钟就可看到一辆从乙站开往甲站的车。所以从甲站到乙站，该旅客在途中看到60÷5-1=11（辆）从乙站开来的车。

74、如果a、b均为质数，且3a+7b=41，则a+b=_____
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:C。a=2，b=5符合题意，选C。

75、某小学六年级的同学要从10名候选人中投票选举三好学生，规定每位同学必须从这10个人中任选两名，那么至少有_____人参加投票，才能保证必有不少于5个同学投了相同两个候选人的票。
A: 256B: 241C: 209D: 181
参考答案: D 本题解释:【解析】从10人中选2人，共有45种不同的选法。要保证至少有5个同学投了相同两个候选人的票，由抽屉原理知，至少要45×4+1=181人。

76、有100人参加运动会的三个比赛项目，每人至少参加一项，其中未参加跳远的有50人，未参加跳高的有60人，未参加赛跑的有70人。问至少有多少人参加了不止一个项目？_____
A: 7B: 10C: 15D: 20
参考答案: B 本题解释:【解析】B。最值问题。由题意，参加跳远的人数为50人，参加跳高的为40人，参加赛跑的为30人；即参加项目的人次为120人次；故欲使参加不止一项的人数最少，则需要使只参加一项的人数最多为x，参加3项的人数为y；故x+3y=120，x+y=100，解得y=10。

77、把一个边长为4厘米的正方形铁丝框拉成两个同样大小的圆形铁丝框，则每个圆铁丝框的面积为_____。
A: AB: BC: CD: D
参考答案: D 本题解释:D【解析】设铁丝拉成的圆的半径为r，则4×4=2×2πr，r=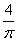，圆形面积S=πr2=。

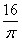78、药厂使用电动研磨器将一批晒干的中药磨成药粉。厂长决定从上午10点开始，增加若干台手动研磨器进行辅助作业。他估算如果增加2台，可在晚上8点完成，如果增加8台，可在下午6点完成。问如果希望在下午3点完成，需要增加多少台手工研磨器？_____
A: 20B: 24C: 26D: 32
参考答案: C 本题解释:【答案】C。解析：设原有电动研磨器为N台，需要增X台手工研磨器，根据牛吃草公式有：Y=(N+2)10;Y=(N+8)8，解得N=22，Y=240;代入Y=(N+X)5解得X=26，故选择C选项。

79、甲、乙、丙三人买书共花费96元钱，已知丙比甲多花16元，乙比甲多花8元，则甲、乙、丙三人花的钱的比是_____。
A: 3:5:4B: 4:5:6C: 2:3:4D: 3:4:5
参考答案: D 本题解释:D【解析】设甲花的钱为x，则x+（x+16）+（x+8）=96，则x=24。故三人花的钱的比为24:32:40=3:4:5。

80、某机关单位召开一次会议预期12天，后因会期缩短4天，因此原预算费用节约了一部分。其中生活费一项节约了4000 ，比原计划少用40%，生活费预算占总预算的4/9，则总预算为_____。
A: 45000元：B: 35000元C: 27500元D: 22500元
参考答案: D 本题解释:D【精析】生活费比计划少用40%，因此计划中的生活费为4000÷40%=10000元。该项费用占总预算的9/4因此总预算为10000×9/4=22500元。

81、三个单位共有180人，甲、乙两个单位人数之和比丙单位多20人，甲单位比乙单位少2人，求甲单位的人数_____
A: 48人B: 49人C: 50人D: 51人
参考答案: B 本题解释:【答案】B，列方程即可求解

82、某种皮衣定价是1150元，以8折售出仍可以盈利15%，某顾客在8折的基础上要求再让利150元，如果真是这样，商店的盈亏情况是：_____
A: 亏20元B: 赚20元C: 亏30元D: 赚30元
参考答案: C 本题解释:【答案】C。解析：该皮衣的成本为1150×0.8÷（1+15%）=800元，在8折的基础上再让利150元的收入为1150×0.8-150=770元，所以商店会亏损800-770=30元。

83、四年级学生搬砖，有12人每人各搬7块，有20人每人各搬6块，其余的每人搬5块，这样最后余下148块;如果有30人每人各搬8块，有8人每人搬9块，其余的每人搬10块，这样分配最后余下20块。学生共有多少人?_____
A: 80B: 76C: 48D: 24
参考答案: C 本题解释:C【解析】每人如果都搬5块，则共余下的块数：（7-5）×12+（6-5）×20+148=192（块）;把另一种分配方法改为，每人都搬10块，则砖总数不足：（10-8）×30+（10-9）×8-20=48（块）。设学生人数为x，则：5x+192=10x-48，故x=48（人）。

84、有两只相同的大桶和一只空杯子，甲桶装牛奶，乙桶装糖水，先从甲桶内取出一杯牛奶倒入乙桶，再从乙桶取出一杯糖水和牛奶的混合液倒人甲桶，请问，此时甲桶内的糖水多还是乙桶内的牛奶多?_____。
A: 无法判定B: 甲桶糖水多C: 乙桶牛奶多D: 一样多
参考答案: D 本题解释:D【精析】假设乙桶内有N杯糖水，从甲中取出1杯牛奶倒入乙桶，乙桶中有l杯牛奶和N杯糖水。均匀后，再从乙桶取出一杯糖水和牛奶的混合物倒入甲桶，这杯混合物中有牛奶1/N+1杯有糖水N/N+1杯,因此乙桶中剩余的牛奶有N/N+1杯，而倒入甲桶中的糖水也有而N/N+1杯。甲桶内的糖水和乙桶内的牛奶一样多。

85、将700克14.3%的盐水与900克11.1%的盐水混合后，再加入200克盐，蒸发掉300克水后，该盐水的浓度为_____。
A: 22.2%B: 24.3%C: 26.7%D: 28.6%
参考答案: C 本题解释:【答案】C。解析：由题意可得，最后该盐水浓度为（700×14.3%＋900×11.1%＋200）÷（700＋900＋200－300）＝400÷1500≈26.7%。故正确答案为C。

86、某乐队举办一场演唱会的收入是7000元,乐队的主唱分得其中的25%,另外5名成员平分余下的收入,那么他们每人分得多少元?_____
A: 1750B: 1400C: 1120D: 1050
参考答案: D 本题解释:【答案】D。解析:主唱分25%,其余5人分75%,所以每人分15%,所以7000×l5%=1050元。

87、有一个矩形花园,长比宽多30米,现在花园的四周铺等宽的环路。已知路的面积是800M2,路的外周长是180m,问路宽是多少米?_____
A: 4B: 5C: 6D: 3
参考答案: B 本题解释:【答案】B。解析:设小矩形的宽是x,则长是x+30;设路宽是y,则大矩形的宽是x+2,大矩形的长是x+30+2y,已知条件可表示为(x+2y)(x+30+27)-x(x+30)=800和2(x+2y+x+30+2y)=180,解得y=5米。

88、一单位组织员工乘坐旅游车去泰山，要求每辆车上的员工人数相等。起初，每辆车上乘坐22人，结果有1人无法上车；如果开走一辆空车，那么所有的游客正好能平均乘到其余各辆旅游车上，已知每辆车上最多能乘坐32人。请问该单位共有多少员工去了泰山？_____
A: 269B: 352C: 478D: 529
参考答案: D 本题解释:D。开走一辆空车，则剩余22+1=23人，需要把23人平均分配到剩余的旅游车上。23的约数只有23和1，而每辆车最多能乘坐32人，排除将23人分配到1辆车上的情况（22+23>32），只能每辆车上分配1人，分配后每辆车有22+1=23人。进行条件转换，如果没有开走那辆车，那么每辆车分配23人，还少23人，加上已有条件“每辆车上乘坐22人，结果有1人无法上车”，就转化成了常规的盈亏问题。有车（1+23）÷（23-22）=24辆。有员工24×22+1=529人。

89、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:D【解析】首先目测可以知道3/7、17/35和101/203都小于1/2，而4/9和151/301都大于1/2，所以只要比较二者的大小就可以，通过计算，151/301大，所以选择D。

90、某数的百分之一等于0.003，那么该数的10倍是多少?_____。
A: 0.003B: 0.03C: 0.3D: 3
参考答案: D 本题解释:D【解析】某数的百分之一为0.003，则该数为0.3，那么它的10倍为3。故正确答案为D。

91、校对一份书稿，编辑甲每天的工作效率等于编辑乙、丙每天工作效率之和，丙的工作效率相当于甲、乙每天工作效率之和的1/5。如果三人一起校对只需6天就可完成。现在如果让乙一人单独校对这份书稿，则需要_____天才能完成。
A: 20B: 16C: 24D: 18
参考答案: D 本题解释:D【解析】三人一起完成校对需要6天，那么三人每天的效率之和是1/6。因为甲每天的工作效率等于乙、丙每天工作效率之和，那么甲的工作效率为1/12，乙、丙的效率和也是1/12。设乙单独完成校对需要x天，那么根据题意可得到方程：1/12-（1/x）=（1/12+1/x）×（1/5）解得x=18,即乙单独完成校对需要18天，正确答案为D。

92、现有一批货物共37吨需要运输，有两种货车供选择，其中大车载重7吨，小车载重4吨，现需一次拉完且车都满载，问共需大小货车多少辆？_____
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:【答案】C。解析：设需要大、小货车各x、y辆，依题意有7x+4y＝37。7÷4＝1…3，37÷4=9…1，因此x不能为1。x=3时，解得y＝4，符合题意，需要的货车数量为3+4＝7(辆)。

93、一个数能被3、5、7整除，若用11去除这个数则余1，这个数最小是多少?_____
A: 105B: 210C: 265D: 375
参考答案: B 本题解释:B。这个数能被3、5、7整除，因此这个数是105的倍数.若这个数是105，105除以11的余数是6，不符合题意；若这个数是105×2＝210，210除以11的余数是1，满足题意。因此这个数最小是210。

94、如果某商店 以每打1.8元的价格购进6打小工艺品(每打12件).之后又以每件0.2元卖出.这些小商品全部卖完后商店可得多少利润？_____
A: 32元 B: 3.6元 C: 2.4元 D: 2.84元
参考答案: B 本题解释:B【解析】0.2×12×6-1.8×6=3.6，一打=12个。

95、100个孩子按1、2、3……依次报数，从报奇数的人中选取k个孩子，他们所报数字之和为1949，问k最大值为多少?_____
A: 43B: 44C: 45D: 46
参考答案: A 本题解释:【答案】A。解析：奇数个奇数的和为奇数，故k的最大值应是奇数，排除B、D;从1开始，45个连续奇数的和是452>1949，排除C，此题答案为A。

96、两个相同的瓶子装满酒精溶液，一个瓶子中酒精与水的体积比是3:1，另一个瓶子中酒精与水的体积比是4:1，若把两瓶酒精溶液混合，则混合后的酒精和水的体积之比是多少?_____
A: 31:9B: 7:2C: 31:40D: 20:11
参考答案: A 本题解释:【答案解析】(3/4+4/5)/(1/4+1/5)=31：9

97、甲、乙有数量相同的萝卜，甲打算卖1元2个，乙打算卖1元3个，如甲、乙二人一起按2元5个卖全部的萝卜，总收入会比预想的1个人少4元，两人共有多少萝卜？_____
A: 420B: 120C: 360D: 240
参考答案: D 本题解释:D。

98、有a、b、c三个数，已知a×b=24，a×c=36，b×c=54，求a+b+c=_____
A: 23B: 21C: 19D: 17
参考答案: C 本题解释: C 解析：此题最好用猜证结合法。试得a、b、c分别为：4、6、9，故选C。若要正面求解：则由前两个式子可得b=2c/3，代入第三个式子可得c=9，进而求得a=4，b=6。,a2=24×36÷54=16，所以a=4，则b=6，c=9，故a+b+c=19。

99、一块试验田，以前这块地所种植的是普通水稻。现在将该试验田的1/3种上超级水稻，收割时发现该试验田水稻总产量是以前总产量的1.5倍。如果普通水稻的产量不变，则超级水稻的平均产量与普通水稻的平均产量之比是_____。
A: 5∶2B: 4∶3C: 3∶1D: 2∶1
参考答案: A 本题解释:答案：A。设该试验田种普通水稻产量为x，种超级水稻产量为y，则有，解得y∶x=5∶2。

100、从1、2、3、4中任取3个数组成没有重复的三位数的偶数的取法种数为_____。
A: 10 　 B: 12 　 C: 13 　 D: 11
参考答案: B 本题解释:【解析】B。 题干要求组成没有重复数字的三位数的偶数，所以只有尾数是2或4两种情况。当尾数是2时，有2×3=6（种）；当尾数是4时，有2×3=6（种），所以共有6+6=12（种），故本题答案为B。