1、假设7个相异正整数的平均数是14，中位数是18，则次7个正整数中最大数是多少？_____
A: 58B: 44C: 35D: 26
参考答案: C 本题解释:【答案】C。解析：构造数列问题。此题告诉我们平均数是14，则总和为14*7=98，中位数为18，总共7个数，意味着小于18的有3个数，大于18的有3个数，为了保证最大的数大，所以我们要让大于18的数尽可能的小，则其他的两个数我们可以定义为19，20；所以得到的式子为18+19+20+n<98，所以n<41，则小于41的最大选项为35，所以选择C选项。

2、一个快钟每小时比标准时间快1分钟，一个慢钟每小时比标准时间慢3分钟。如将两个钟同时调到标准时间，结果在24小时内，快钟显示10点整时，慢钟恰好显示9点整。则此时的标准时间是_____。
A: 9点15分B: 9点30分C: 9点35分D: 9点45分
参考答案: D 本题解释:【答案解析】使用代入法，设经历了X个小时，标准时间为Y，那么10-X=Y，9+3X=Y,将选项代入，即可得出结论。

3、10个连续偶数的和是以1开始的10个连续奇数和的2.5倍，其中最大的偶数是多少?
A: 34B: 38C: 40D: 42
参考答案: A 本题解释:【答案】A。解析：猜证结合，以1开始的10个连续奇数的和是250，代入答案中得A。

4、某市现有70万人口，如果5年后城镇人口增加4%，农村人口增加5.4%，则全市人口将增加4.8%，那么这个市现有城镇人口_____。
A: 30万B: 31.2万C: 40万D: 41.6万
参考答案: A 本题解释:【答案解析】可以设现有城镇人口为X万，那么农村人口为70-X，得出等式4%×X+5.4%×(70-X)=70×4.8%，解出结果为30。

5、小明用5天时间看完了一本200页的故事书。已知第二天看的页数比第一天多，第三天看的页数是第一、二两天看的页数之和，第四天看的页数是第二、三两天看的页数之和，第五天看的页数是第三、四两天看的页数之和。那么小明第五天至少看了_____页。
A: 84B: 78C: 88D: 94
参考答案: A 本题解释:【答案】A。解析：设小明第一天看了a页，第二天看了b页，则前五天看的页数依次为a，b，a+b，a+2b，2a+3b。这些数的和是200，可得5a+7b=200。因为5a与200都是5的倍数，所以b是5的倍数。因为ba，所以上式只有两组解b=20，a=12；b=25，a=5。将这两组解分别代入2a+3b，得到第五天至少看了84页。

6、真分数a/7化为小数后，如果从小数点后第一位数字开始连续若干数字之和是1992，那么A的值是_____。
A: 6B: 5C: 7D: 8
参考答案: A 本题解释:【答案解析】：由于除7不能整除的的数结果会是‘142857’的循环(这个可以自己测算一下)，1+4+2+8+5+7=27，1992/27余数为21，重循环里边可知8+5+7+1=21，所以8571会多算一遍(多重复的一遍，一定在靠近小数点的位置上)，则小数点后第一位为8，因此a为6。

7、某天体沿正圆形轨道绕地球一圈所需时间为29.53059天，转速约1公里／秒。假设该天体离地球的距离比现在远10万公里而转速不变，那么该天体绕地球一圈约需要多少天？_____
A: 31 B: 32 C: 34 D: 37
参考答案: D 本题解释: D。算式为[29.53059×24×60×60×1/π+100000×2]×π÷1÷60÷60÷24≈36.8天，所以答案为D项。

8、地球表面的陆地面积和海洋面积之比是29︰71，其中陆地的四分之三在北半球，那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释:【解析】D。根据题干中的比例关系，可以推断出南、北半球的海洋面积之比为：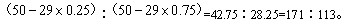

9、某公司招聘甲、乙两种职位的人员共90人，甲、乙两种职位人员每月的工资分别为1500元和2500元，若甲职位的工资总支出是乙职位的40%，则乙职位招聘人数比甲职位多：_____
A: 24人B: 20人C: 18人D: 15人
参考答案: C 本题解释:【答案】C。解析：设甲职位有x人，则Z乙职位有（90-x）人。依题意有l500x=2500×（90-x）×40%，x=36人。因此乙职位有90-36=54人，比甲职位多54-36=18人。快速突破甲、乙职位的人均工资之比为1500：2500=3：5;甲职位的工资总支出是乙职位的40%，则甲、乙职位的总工资支出之比为40%：1=2：5，所以甲、乙职位的招聘人位之比为2/3：5/5=2：3，甲、乙共招聘90人，则乙职位招聘人数比甲职位多90×（3-2）/（3+2）=18人。

10、小明和小红积极参加红领巾储蓄活动，把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品，那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元？_____
A: 44B: 64C: 75D: 86
参考答案: B 本题解释:【答案】B。解析：设小明原来存了Y元，则小红存了Y＋20元，根据题意得（Y－12）×3＝（Y＋20－12），解得Y＝22元。因此两人原来共存了2Y＋20＝64元，故正确答案为B。

11、用数字0，1，2(既可全用也可不全用)组成的非零自然数，按从小到大排列，问“1010”排在第几个?_____
A: 30B: 31C: 32D: 33
参考答案: A 本题解释:本题实际求由0，1，2构成的数字中，小于1010的有多少个。位数不固定，先按位数分类，再对每类进行计数。显然组成的非零一位数有2个;两位数有2×3=6（个）;三位数有2×3×3=18（个）;四位数中比1010小的为1000，1001，1002共计3个。故1010排在第30位。故选A。

12、某种茶叶原价30元一包，为了促销，降低了价格，销量增加了二倍，收入增加了五分之三，则一包茶叶降价_____元。
A: 12B: 14C: 13D: 11
参考答案: B 本题解释:【答案】B。解析：设原来茶叶的销量为1，那么现在销量为3，原来收入为30元，现在收入为30×（1+3/5）=48元，每包茶叶为48÷3=16元，降价30-16=14元。

13、在所有的两位数中,十位数字比个位数字大的两位数共有多少个?_____
A: 49B: 50C: 56D: 45
参考答案: D 本题解释:【答案】D。解析:十位是9的有9个,十位是8的有8个,……十位是1的有1个,共有:1+2+3+……+9=45个。故应选择D。

14、把黑桃、红桃、方片、梅花四种花色的扑克牌按黑桃10张、红桃9张、方片7张、梅花5张的顺序循环排列。问第2015张扑克牌是什么花色？_____
A: 黑桃 B: 红桃 C: 梅花 D: 方片
参考答案: C 本题解释:【答案】C。解析：一个完整的循环包括黑桃10张，红桃9张，方片7张，梅花5张，共31张，2015÷31=65，刚好可以被31整除，因此第2015张牌是梅花。正确答案为C。

15、桌面上有两个半径分别为2厘米和40厘米的圆环，让小圆环沿着大圆环外边缘滚动一圈，则小圆环滚动的圈数是：_____
A: 9B: 25C: 49D: 81
参考答案: B 本题解释:【答案解析】如果两人不调头走，两人相遇需要1350÷1000÷(4+5)×60=9分钟。如果以初始方向为正方向，则两个人分别走了1、-3、5、-7、……分钟的路程，由于9=1-3+5-7+9-11+13-15+17，则出发后1+3+5+7+9+11+13+15+17=81分钟两人相遇。

16、某种灯泡出厂售价为6.2元，采用新的生产技术后可节约12％的成本，若售价不变，利润可比原来增长50％。问该产品最初的成本为多少元？_____
A: 3.8B: 4.5C: 5.0D: 5.5
参考答案: C 本题解释:【答案】C。解析：设原来的成本为x元，那么6.2一0.88x=（1+0.5）（6.2一x），解得x=5。故选C。

17、甲乙丙的速度之比为3：4：5，经过相同的一段路，三人所用时间之比：_____
A: 3：4：5　 B: 5：4：3 C: 20：15：12 D: 12：8：5
参考答案: C 本题解释:C【解析】根据公式“时间=路程÷速度”可知，经过相同的路程，甲、乙、丙的时间比为1/3:1/4:1/5=20:15:12。

18、一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍。如果评一、二、三等奖各两人，那么每个一等奖金是308元;如果评一个一等奖，三个三等奖，两个二等奖，那么一等奖的奖金是多少元_____
A: 154B: 196C: 392D: 490
参考答案: C 本题解释:【答案解析】①每个二等奖奖金为：308÷2=154(元)。②每个三等奖奖金为：154÷2=77(元)。③一共有奖金：(308+154+77)×2=1078(元)。④设一个三等奖奖金为x元，则一个二等奖奖金为2x元，一个一等奖奖金为4x元，列方程得：4x+4x+3x=1078，x=98。一等奖奖金为：98×4=392(元)。故正确答案为C。

19、将一块三角形绿地沿一条直线分成两个区域，一块为三角形，一块为梯形，已知分出的三角形区域的面积为1.2亩，梯形区域的上、下底边分别为80米、240米，问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:本题答案选A。解析：分出的三角形面积为1.2亩＝800平方米，底边为梯形的上底边80米可知三角形的高为800×2÷80＝20米，整块三角形绿地的底边为240米，由比例关系可得，高为20÷（80÷240）＝60米，则绿地面积为240×60÷2＝7200平方米＝10.8亩，故梯形面积为10.8-1.2＝9.6亩。

20、一个学雷锋小组的大学生们每天到餐馆打工半小时，每人可挣3元钱。到11月11日，他们一共挣了1764元。这个小组计划到12月9日这天挣足3000元捐给“希望工程”。因此小组必须在几天后增加一个人。增加的这个人应该从11月_____日起每天到餐馆打工，才能到12月9日恰好挣足3000元钱。
A: 18B: 24C: 14D: 20
参考答案: D 本题解释:D[解析]还缺3000-1764=1236（元），从11月12日～12月9日还有30+9-12+1=28（天），这28天中，（原来小组中）每人可挣3×28=84（元）。因为1236÷84=14……60，所以原有14人，必须增加一个人挣60元。60÷3=20（天），30+9-20+1=20，所以增加的这个人应该从11月20日起去打工。

21、一杯糖水，第一次加入一定量的水后，糖水的含糖百分比变为15%；第二次又加入同样多的水，糖水的含糖百分变比为12%；第三次再加入同样多的水，糖水的含糖百分比将变为多少？_____
A: 8%B: 9%C: 10%D: 11%
参考答案: C 本题解释:【答案】C。解析：故正确答案为C。

22、在1至100这100个数中，有既不能被5整除也不能被9整除的数，它们的和是_____。
A: 1644B: 1779C: 3406D: 3541
参考答案: D 本题解释:【答案解析】先求出被5或9整除的数的和。1至100中被5整除的数有5，10，15，…，100，和为5+10+15+…+100=(100+5)×20÷2=10501至100中被9整除的数有9，18，…，99，和为9+18+27+…+99=(9+99)×11÷2=594又因为1～100中，45，90这两个数同时被5与9整除，于是所求的和是(1+2+…+100)-(5+10+…+100)-(9+18+…+99)+(45+90)=3541。因此，本题正确答案为D。

23、

24、某机关共有干部、职工350人，其中55岁以上共有70人。现拟进行机构改革，总体规模压缩为180人，并规定55岁以上的人裁减比例为70％。请问55岁以下的人裁减比例约是多少?_____。
A: 51％ B: 43％ C: 40％ D: 34%
参考答案: B

25、二十几个小朋友围成一圈，按顺时针方向一圈一圈地连续报数。如果报2和200的是同一个人，那么共有_____个小朋友。
A: 22B: 24C: 27D: 28
参考答案: A 本题解释:A【解析】小朋友的人数应是(200-2)=198的约数，而198=2×3×3×11。约数中只有2×11=22符合题意。

26、小王的爷爷比奶奶大2岁，爸爸比妈妈大2岁，全家五口人共200岁。已知爷爷年龄是小王的5倍，爸爸年龄在4年前是小王的4倍，则小王的爸爸今年多少岁? _____
A: 40B: 36C: 32D: 44
参考答案: B 本题解释:B。假设奶奶和爷爷一样大，妈妈和爸爸一样大，全家年龄和是200+4=204岁，这样爷爷、奶奶的年龄和是10个小王的年龄。而爸爸的年龄是4年前小王的4倍多4岁，换句话说，就是比现在小王年龄的4倍少4×4-4=12岁，妈妈也比现在小王的年龄的4倍少12岁，这样现在全家人的年龄和204+12+12=228岁，则小王的年龄为228÷（5×2+4×2+1）=12岁，爸爸的年龄为（12-4）×4+4=36岁。

27、某地区水电站规定，如果每月用电不超过24度，则每度收9分钱；如果超过24度，则多出度数按每度2角收费，若某月甲比乙多交了9.6角，则甲交了几角几分？_____
A: 27角6分B: 26角4分C: 25角5分D: 26角6分
参考答案: A 本题解释:【解析】A。如果每月用电24度，则应该交24×9＝216分钱，即21.6角。答案中没有这个答案，就是说甲已经超过了这个规定数字。设他用了24＋M度电，则交了24×9+M×20＝216＋20×M，甲比乙多交了96分，则216＋20×M－96可以被9整除，即（20×M+120）÷9。M＝3时，（20×M＋120）÷9＝2，即甲用了27度电，用了276分。

28、某单位今年一月份购买5包A4纸、6包B5纸，购买A4纸的钱比B5纸少5元;第一季度该单位共购买A4纸15包、B5纸12包、共花费510元;那么每包B5纸的价格比A4纸便宜_____。
A: 1.5元B: 2.0元C: 2.5元D: 3.0元
参考答案: C 本题解释:C【解析】方程问题。设A4纸和B5纸的价格分别为x元和y元。由题意可得方程，6y-5x=5,15x+12y=510解得x=20，y=17.5,所以每包纸比A4纸便宜20-17.5=2.5元。答案选择C选项。

29、有浓度为4%的盐水若干克，蒸发了一些水分后浓度变成l0%，再加入300克4%的盐水后，变为浓度6.4%的盐水，则最初的盐水是_____
A: 200克B: 300克C: 400克D: 500克
参考答案: D 本题解释: 【解析】D。可以采用带入法，将选项代入题干中，发现只有当最初的盐水是500克的时候才能满足要求，或者利用倒推方法解题。

30、一条长度为30米、宽度为3米的未划停车位的路边，最差的情况也可以停2米宽、3米长的汽车多少辆?_____
A: 5辆B: 7辆C: 8辆D: l5辆
参考答案: A 本题解释:【解析】分三种情况:第一种:汽车如果与道路垂直。每辆车的车距应尽可能的大，但距离必须小于2米（否则可以再停一辆），当两辆车的车距为2米时，最少可停（30-2）÷（2+2）=7（辆），那么最差的情况下至少可以停8辆车;第二种:汽车如果与道路平行。每辆车的车距应尽可能的大，但距离小于3米，当两辆车的车距为3米时，最少可停（30-3）÷（3+3）=4.5（辆），即停5辆。第三种:汽车与道路有平行与垂直两种情况并存，则停的汽车数量应介于5辆和8辆之间。而题干是问的最差的情况，故最少停5辆车。

31、某储户于1999年1月1日存入银行60 000元，年利率为2.00％，存款到期日即2000年1月1日将存款全部取出，国家规定凡1999年11月1日后孳生的利息收入应缴纳利息税，税率为20%，则该储户实际提取本金合计为_____。
A: 61 200元 B: 61 160元C: 61 00 0元 D: 60 040元
参考答案: B

32、南阳中学有语文教师8名、数学教师7名、英语教师5名和体育教师2名。现要从以上四科教师中各选出1名教师去参加培训，问共有几种不同的选法_____
A: 96种 B: 124种 C: 382种 D: 560种
参考答案: D 本题解释:【解析】D。根据乘法原理，各选1名的选法共有8×7×5×2＝560（种）。

33、一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是_____
A: 74B: 148C: 150 D154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是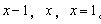。那么有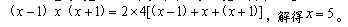所以这个长方体的表面积为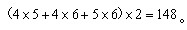

34、已知一列货运火车通过500米的隧道用了28秒，接着通过374米的隧道用了22秒，这列货运火车与另一列长96米的客运火车相对而过，用了4秒钟，问这列客运火车的速度是多少? _____
A: 21米/秒B: 25米/秒C: 36米/秒D: 46米/秒
参考答案: B 本题解释:B。通过题干前两个条件可以先求出货运火车的速度为（500-374）÷（28-22）=21米/秒，则该货运火车的长度为21×22-374=88米。货车与客车相对而过，此时总路程是两车车长的总和，则两车的速度和为（96+88）÷4=46米/秒，客车的速度即为46-21=25米/秒。

35、李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到。0.5小时后，营地老师闻讯前往迎接，每小时比李华多走1.2千米。又过了1.5小时，张明从学校骑车去营地报到。结果3人同时在途中某地相遇。问：张明每小时的速度是多少千米?_____
A: 25B: 50C: 30D: 20
参考答案: D 本题解释:D老师速度=4+1.2=5.2千米/时，与李华相遇时间是老师出发后(20.4-4×0.5)÷(4+5.2)=2小时，相遇地点距离学校4×(0.5+2)=10千米，所以张明的速度=10÷(2-1.5)=20千米/时。

36、对某单位的100名员工进行调查，结果发现他们喜欢看球赛和电影、戏剧。其中58人喜欢看球赛，38人喜欢看戏剧，52人喜欢看电影，既喜欢看球赛又喜欢看戏剧的有18人，既喜欢看电影又喜欢看戏剧的有16人，三种都喜欢看的有12人，则只喜欢看电影的有_____。
A: 22人B: 28人C: 30人D: 36人
参考答案: A 本题解释:【答案解析】本题可以使用阴影覆盖法，即100-(40+18+20)=22(人)，故远A项。

37、小木、小林、小森三人去看电影，如果用小木带的钱去买三张电影票，还差0.55元;如果用小林带的钱去买三张电影票，还差0.69元;如果用三人带去的钱买三张电影票，就多0.30元，已知小森带了0.37元，那么买一张电影票要用多少元?_____
A: 1.06B: 0.67C: 0.52D: 0.39
参考答案: D 本题解释:D【解析】设每张电影票x元，则小木的钱数为3x-0.55元，小林的钱数为3x-0.69元，小森的钱数为0.37元。三人的钱数和为3x+0.30元，即可得出：3x-0.55+3x-0.69+0.37=3x+0.30，求得x=0.39（元）。

38、妈妈给了红红一些钱去买贺年卡，有甲、乙、丙三种贺年卡，甲种卡每张0.50元，丙种卡每张1.20元。用这些钱买甲种卡要比买乙种卡多买8张，买乙种卡要比买丙种卡多买6张。妈妈给了红红多少钱?_____
A: 8元B: 10元C: 12元D: 15元
参考答案: C 本题解释:C解析：盈亏总额为0.5×8+1.2×6=11.2（元），单价相差1.2-0.5=0.7（元），所以共可买乙种卡11.2÷0.7=16（张）。妈妈给了红红0.5×（16+8）=12（元）。故本题正确答案为C。

39、某工厂有一大型储水罐供全厂生产用水，已知每天晚8点至早8点蓄水，蓄水管流量为8吨/小时，工厂用水为每天早8点至晚12点，用量为6吨/时，储水罐中水位最高时的储水量至少是_____。
A: 48吨B: 72吨C: 84吨D: 96吨
参考答案: B 本题解释:B【解析】从每晚8点开始蓄水，至早8点水位一直在升高，在这之后，蓄水停止，水位下降;晚8点至晚12点之间，水位上升，但同时仍在用水。故水位最高点应为早8点。8×（12一4）+4×（8一6）=72（吨）。

40、某商店以每件6元的进价买回一批商品，售价为每件8.4元，当卖了这批商品的3/4时，不仅收回了购买这批商品所付的款项，而且还获得利润90元，这批商品有多少件？_____
A: 500 　 B: 600 　 C: 300 　 D: 400
参考答案: C 本题解释:【解析】C。 设这批商品有x件，可列方程：x×6=34x×8.4－90，解得x=300，所以本题答案为C。

41、某校学生列队以8千米/小时的速度前进，在队尾，校长让一名学生跑步到队伍的最前面找带队的老师传达一个命令，然后立即返回队尾，这位学生的速度为12千米/小时，从队伍出发赶到排头又回到队尾共用了7.2分钟，那么学生的队伍长_____米。
A: 360B: 400C: 450D: 500
参考答案: B 本题解释:B【解析】8千米/小时=（400/3）米/分，12千米/小时=200米/分，设队伍长χ米，则χ÷（200-400/3）+χ÷（200+400/3）=7.2，解得χ=400。

42、如果某商店 以每打1.8元的价格购进6打小工艺品(每打12件).之后又以每件0.2元卖出.这些小商品全部卖完后商店可得多少利润？_____
A: 32元 B: 3.6元 C: 2.4元 D: 2.84元
参考答案: B 本题解释:B【解析】0.2×12×6-1.8×6=3.6，一打=12个。

43、一百张牌抽掉奇数牌，然后再抽掉剩下牌中位于奇数位的牌……如此最后剩下的一张是原来100张牌排序中的第几张呢？_____
A: 63 B: 64 C: 65 D: 66
参考答案: B 本题解释:B

44、某技校安排本届所有毕业生分别去甲、乙、丙3个不同的工厂实习。去甲厂实习的毕业生占毕业生总数的32%,去乙厂实习的毕业生比甲厂少6人，且占毕业生总数的24%.问去丙厂实习的人数比去甲厂实习的人数_____。
A: 少9人B: 多9人C: 少6人D: 多6人
参考答案: B 本题解释:【答案】B。解析：根据题意去甲厂实习的人数占32%,去乙厂实习的人数占24%,因此去丙厂实习的人数占1-32%-24%=44%,故去丙厂的人数比去甲厂多44%-32%=12%;而去甲厂实习的人数比去乙厂的多32%-24%=8%,为6人，故去丙厂的人数比去甲厂的应多6÷8%×12%=9人，故答案选B。

45、某小学六年级的同学要从10名候选人中投票选举三好学生，规定每位同学必须从这10个人中任选两名，那么至少有_____人参加投票，才能保证必有不少于5个同学投了相同两个候选人的票。
A: 256B: 241C: 209D: 181
参考答案: D 本题解释:【解析】从10人中选2人，共有45种不同的选法。要保证至少有5个同学投了相同两个候选人的票，由抽屉原理知，至少要45×4+1=181人。

46、有一笔奖金，按1：2：3的比例来分，已知第三人分450元，那么这笔奖金总共是_____元。
A: 1150 B: 1000 C: 900 D: 750
参考答案: C 本题解释:C。根据题意可知，这笔奖金共分为6份，而分到3份的第三人拿到了450元，则6份当是450×2=900元。所以正确答案为C项。

47、某种奖券的号码有9位，如果奖券至少有两个非零数字并且从左边第一个非零数字起，每个数字小于它右边的数字，就称这样的号码为“中奖号码”，请问该种奖券的“中奖号码”有_____。
A: 512个B: 502个C: 206个D: 196个
参考答案: B 本题解释:【解析】解一：号码1—9各出现1或0次，按递增顺序排列（前面补0），共产生2×2×2×2×2×2×2×2×2=29个号码，其中无非零数字或仅有1个非零数字的应予排除（共有10种）。所以中奖号码共有512-10=502个。故本题正确答案为B。解二：中奖号码至少有两个非零数字且从左边第一个非零数字起，每个数字小于它右边的数字，则可得出：C29+C39+C49+C59+C69+C79+C89+C99=502，故选B。

48、某单位招待所有若干间房间，现要安排一支考察队的队员住宿，若每问住3人，则有2人无房可住；若每问住4人，则有一间房间不空也不满，则该招待所的房间最多有_____。
A: 5间B: 4间C: 6间D: 7间
参考答案: A 本题解释:A。

49、五人排队甲在乙前面的排法有几种？_____
A: 60B: 120C: 150D: 180
参考答案: A 本题解释: 答案【A】

50、有一串数：1，3，8，22，60，164，448，……;其中第一个数是1，第二个数是3，从第三个数起，每个数恰好是前两个数之和的2倍。那么在这串数中，第2000个数除以9的余数是_____。
A: 1B: 2C: 3D: 4
参考答案: C 本题解释:C。本题属于周期类问题。用数列的前几项除以9取余数，得到138462705138……是一个循环数列，周期T=9。根据周期的公式，2000/9余数为2，因此第2000个数除以9得到的余数是3，所以选择C选项。

51、出租车在开始10千米以内收费10.5元，以后每走1千米，收费1.7元。请问走25千米需收多少钱?_____
A: 20.6元　B: 35元　C: 36.5元D: 36元
参考答案: D 本题解释:D

52、甲、乙、丙三人沿着400米环形跑道进行800米跑比赛，当甲跑1圈时，乙比甲多跑17圈，丙比甲少跑17圈。如果他们各自跑步的速度始终不变，那么，当乙到达终点时，甲在丙前面_____。
A: 85米　B: 90米C: 100米 D: 105米
参考答案: C 本题解释:【解析】C。甲跑 1 圈，乙比甲多跑 17 圈，即 87 圈，丙比甲少跑 17 圈，即 67 圈，则甲、乙、丙三人速度之比为 7 ∶ 8 ∶ 6 。所以，当乙跑完 800 米 时，甲跑了 700 米 ，丙跑了 600 米 ，甲比丙多跑了 100 米 。

53、甲、乙、丙、丁四人今年分别是16、12、11、9岁。问多少年前，甲、乙的年龄和是丙、丁年龄和的2倍?_____
A: 4B: 6C: 8D: 12
参考答案: B 本题解释: 【解析】B。解法一、设x年前满足条件，则（16-x）+（12-x）=[（11-x）+（9-x）]×2;解法二、两组年龄差为8岁（分别作差5+3=8），当第一组为第二组两倍时肯定是16与8岁。现在第一组和为28岁，需要倒退12岁到16岁，需要6年，因为两个人一年一共倒退2岁。

54、某S为自然数，被10除余数是9，被9除余数是8，被8除余数是7，已知100＜S＜1000，请问这样的数有几个？_____
A: 5 B: 4 　 C: 3 　 D: 2
参考答案: D 本题解释:D。【解析】被N除余数是N-1，所以这个数字就是几个N的公倍数-1。10，9，8的公倍数为360n（n为自然数），因为100＜S＜1000，所以有两个数符合条件。

55、筑路队原计划每天筑路720米，实际每天比原计划多筑路80米，这样在规定完成全路修筑任务的前3天，就只剩下1160米未筑，这条路全长多少千米?_____
A: 8.10B: 10.12C: 11.16D: 13.50
参考答案: C 本题解释:C解析：现在每天筑路：720+80=800（米）规定时间内，多筑的路是：（720+80）×3-1160=2400-1160=1240（米）求出规定的时间是1240÷80=15.5（天），这条路的全长是,720×15.5=11160（米）。故本题选C。

56、一袋大白兔奶糖，5块一组分剩余2块，3块一组分剩1块，问这袋糖至少有多少块?_____
A: 26B: 34C: 37D: 43
参考答案: C 本题解释:C【解析】所要求的数必须满足除以5余2，除以3余1，通过代入法，满足条件的只有37，故答案为C。

57、如图所示，半圆与等腰三角形ABC的斜边AC相切，AB=BC=1。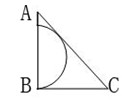问半圆的直径是多少?_____
A: AB: BC: CD: D
参考答案: C 本题解释:C

58、为帮助果农解决销路，某企业年底买了一批水果，平均发给每部门若干筐之后还多了12筐，如果再买进8筐则每个部门可分得10筐，则这批水果共有_____筐。
A: 192B: 198C: 200D: 212
参考答案: A 本题解释:【答案】A。解析：总数加8应能被10整除，如果为A，则部门数为20；如果为D，部门数为22，则212÷22=9……14不符合题意。故选择A。

59、袋子里红球与白球的数量之比为19∶13，放入若干个红球后，红球与白球的数量之比变为5∶3，再放入若干个白球后，红球与白球的数量之比为13∶11，已知放入的红球比白球少80个。那么原来袋子里共有多少个球？_____
A: 650 B: 720 C: 840 D: 960
参考答案: D 本题解释:

60、大小两个数的和是50.886，较大数的小数点向左移动一位就等于较小的数，求较大的数是_____。
A: 46.25B: 40.26C: 46.15D: 46.26
参考答案: D 本题解释:【答案】D。解析：观察选项发现，大数小数点后有两位，因为大小两个数的和是50.886，说明小数小数点后应该有三位，并且尾数为6，排除A、C选项。B选项，40.26小数点左移一位变为4.026，40.26+4.026=44.286≠50.886，排除B选项。D选项，46.26小数点左移一位变为4.626，46.26+4.626=50.886，因此，本题答案为D选项。

61、某玩具店同时卖出一个拼装玩具和一架遥控飞机，拼装玩具66元，遥控飞机120元，拼装玩具赚了10%，而遥控飞机亏本20%，则这个商店卖出这两个玩具赚钱或是亏本多少_____
A: 赚了12元B: 赚了24元C: 亏了14元D: 亏了24元
参考答案: D 本题解释:D【解析】根据题意，拼装玩具赚了66÷(1+10%)×10%=6元，遥控飞机亏本120÷(1-20%)×20%=30元，故这个商店卖出这两个玩具亏本30-6=24元。

62、Ａ、Ｂ两人从同一起跑线上绕300米环形跑道跑步，A每秒钟跑6米，B每秒钟跑4米，问第二次追上B时A跑了多少圈_____
A: 9B: 8C: 7D: 6
参考答案: D 本题解释:D.【解析】因为是环形跑道，当A第一次追上B时，实际上A比B多跑了一圈（300米），当第二次追上B时，A比B则需多跑两圈，共600米。A比B每秒多跑6-4=2（米），多跑600米需时为600÷2=300（秒）时间。所以可列式为：追及距离÷速度差=追及时间。设圈数为x，则x=6米/秒×300秒÷300米/圈=6圈。故本题正确答案为D。

63、某中介服务机构根据服务项目所涉及的金额分段按一定比例收取服务费，具体标准如下：1万元(含)以下收取50元；1万元以上、5万元(含)以下的部分收取3%；5万元以上、10万元(含)以下的部分收取2%.(如某一服务项目所涉及金额为5万元时，应收取服务费1250元。)现有一服务项目所涉及金额为10万元，那么，所收取的服务费应为：_____
A: 2250元 B: 2500元 C: 2750元 D3000元
参考答案: A 本题解释:【解析】分段按比例计算，选A.

64、松鼠妈妈采松果，晴天每天可采20个，雨天每天只能采12个。它一连几天共采了112个松果，平均每天采14个。这几天中有几天下雨?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:【答案解析】松鼠妈妈一连采了松果的天数为：112÷14=8(天)。设雨天有x天，则晴天有(8-x)天，列方程得20×(8-x)+12x=1125×(8-x)+3x=28x=6故本题正确答案为D。

65、一条环形赛道前半段为上坡，后半段为下坡，上坡和下坡的长度相等。两辆车同时从赛道起点出发同向行驶，其中A车上下坡时速相等，而8车上坡时速比A车慢20%，下坡时速比A车快20%。则在A车跑到第几圈时，两车再次齐头并进？_____
A: 22B: 23C: 24D: 25
参考答案: D 本题解释:假定A车速度为v，则B车上坡速度为0.8v，下坡速度为1.2v。由等距离平均速度公式可知B车完成一圈的平均速度为0.96v。则A车与B车跑一圈的平均速度之比为25：24，因此A车完成25圈时，两车同时回到起点。故选D。

66、如下图，梯形ABCD的对角线AC⊥BD，其中AD=1/2，BC=3，AC=2×4/5，BD=2.1。问梯形ABCD的高AE的值是_____。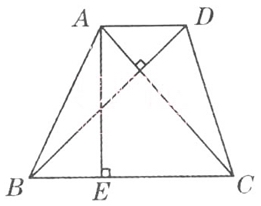
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=（AD+BC）×AE→AE=42/25。

67、3×999+8×99+4×9+15的值是_____。
A: 3866 B: 3855 C: 3840 D: 3877
参考答案: C 本题解释:C。原式转化为3×（1000-1）+×8×（100-1）+4×（10-1）+15=3000-3+800-8+40-4+15=3000+800+40-15+15=3840，所以正确答案为C项。

68、两辆汽车同时从A、B两站相对开出，在B侧距中点20千米处两车相遇，继续以原速前进，到达对方出发站后又立即返回，两车再在距A站160千米处第二次相遇。求A、B两站距离是A_____。
A: 440千米B: 400千米C: 380千米D: 320千米
参考答案: A 本题解释:A[解析]首先，注意到第一次相遇后到第二次相遇时行的路程是出发到第一次相遇时行的路程的2倍。设A、B两站相距x千米，则第一次相遇时，B车行了（0.5x-20）千米;第二次相遇时，B车共行了（0.5x-20）×3（千米），或一个全长又160千米。列方程，得：（0.5x-20）×3=x+160x=440因此，本题正确答案为A。

69、甲、乙两人在一条环形跑道散步，两人从同一点A出发，背向而行。已知甲每分钟步行50米，乙每分钟步行30米，两人第一次在B点相遇，相遇后继续以原来的速度前进，第二次相遇在C点。若B、C两点沿环形跑道的较短距离为150米，则环形跑道的长度为多少米？_____
A: 400B: 450C: 560D: 600
参考答案: A 本题解释:【答案】A。解析：设环形跑道的长度为8x，甲、乙两人的速度比为5：3，则第一次相遇时，甲走的路程为5x、乙走的路程为3x；从第一次相遇到第二次相遇，甲的路程仍然是5x、乙的路程仍然是3x，可得3x＝150，解得x＝50。则环形跑道的长度为80×5＝400（米）。因此，本题选择A选项。

70、某盒灯泡中有3只次品和6只正品(每只均可区分)，测试员每次取出一只进行测试，直到3只次品全部测出为止。假如第三只次品在第六次测试时被发现，那么不同的测试情况共有多少种？_____
A: 43200B: 7200C: 60D: 120
参考答案: B 本题解释:B。

71、试求出下边图形中阴影部分的面积_____。
A: 3B: 2C: 1.5D: 11
参考答案: B 本题解释:【答案】B。解析:图形正中间的正方形边长为2,那么它的面积为4。阴影面积为它的一半,所以是2。

72、四个学生做加法练习，任写一个六位数，然后把个位数字(不等于0)移到这个数的最左边产生一个新的六位数，最后把这个新六位数与原数相加，分别得到以下四个六位数。则哪个结果有可能正确? _____
A: 172536B: 568741C: 620708D: 845267
参考答案: C 本题解释:

73、某班有35个学生，每个学生至少参加英语小组、语文小组、数学小组中的一个课外活动小组。现已知参加英语小组的有17人，参加语文小组的有30人，参加数学小组的有13人。如果有5个学生三个小组全参加了，问有多少个学生只参加了一个小组？_____
A: 15人B: 16人C: 17人D: 18人
参考答案: A 本题解释:A【解析】利用三交集公式A+B+C=AUBUC+AnB+BnC+AnC-AnBnC（AnBnC是指语文，数学，英语三个都参加的人，AUBUC是只总人数），A+B+C=17+30+13，AnBnC=5，AUBUC=35，所求为AUBUC-（AnB+BnC+AnC）+AnBnC。 方便解法：参加一个小组的为x人，两个小组的为y人，x+y+5=35，x+2y+3×5=17+30+13，x=15。

74、某船第一次顺流航行21千米又逆流航行4千米，第二次在同一河道中顺流航行12千米，逆流航行7千米，结果两次所用的时间相等。则顺水船速与逆水船速之比是_____。(设船本身的速度及水流的速度都是不变的)
A: 4∶1B: 3∶1C: 2∶1D: 9∶1
参考答案: B 本题解释:B 【解析】船第一次顺流航行21千米，第二次顺流航行12千米，21-12=9，也就是第一次顺流多用了航行9千米所用的时间，第二次逆流比第一次多用时间于3千米的航行上，总的两次时间相等。就是顺流9千米用的时间等于逆流3千米所用的时间。顺流船速：逆流船速=（21-12）∶（7-4）=3∶1，即顺水船速是逆水船速的3倍。

75、两个运输队，第一队有320人，第二队有280人，现因任务变动，要求第二队的人数是第一队人数的2倍，需从第一队抽调多少人到第二队?_____
A: 80人B: 100人C: 120人D: 140人
参考答案: C 本题解释:C设需抽调x人，根据题意可得2（320-x）=280+x，解得x=120人。

76、计算19961997×19971996-19961996×19971997的值是_____。
A: 0B: 1C: 10000D: 100
参考答案: C 本题解释:C【解析】原式=(19961996+1)×19971996-19961996×(19971996+1)=19971996-19961996=10000

77、小张和小王同时骑摩托车从A地向B地出发，小张的车速是每小时40公里，小王的车速是每小时48公里。小王到达B地后立即向回返，又骑了15分钟后与小张相遇。那么A地与B地之间的距离是多少公里？_____
A: 144B: 136C: 132D: 128
参考答案: C 本题解释:C。相遇的时候小王比小张多走了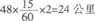，共用时24÷(48-40)=3小时，所以A地与B地之间的距离为48×3-12=132公里。

78、某公司采取百分制对员工进行绩效考核，在12月的考核中，男员工的平均分数为80分，女员工的平均分数为84.25分，而全公司的平均分数为82.5分，如果该公司员工人数多于80人而小于90人，那么该公司男员工和女员工的人数分别为多少？_____
A: 35、50B: 50、35C: 40、45D: 45、40
参考答案: A 本题解释:A。

79、在春运高峰时，某客运中心售票大厅站满等待买票的旅客，为保证售票大厅的旅客安全，大厅入口处旅客排队以等速度进入大厅按次序等待买票，买好票的旅客及时离开大厅。按照这种安排，如果开10个售票窗口，5小时可使大厅内所有旅客买到票;如果开12个售票窗口，3小时可使大厅内所有旅客买到票，假设每个窗口售票速度相同。由于售票大厅入口处旅客速度增加到原速度的1.5倍，为了在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为_____个。
A: 15B: 16C: 18D: 19
参考答案: C 本题解释:C。设每个窗口的服务速度为x人/小时，大厅入口处旅客速度为y人/小时，大厅内乘客有s人。开10个售票窗口，5小时可使大厅内所有旅客买到票，说明s+5y=5×10x;开12个售票窗口，3小时可使大厅内所有旅客买到票，说明s+3y=3×12x;y=72，s=15x。大厅入口处旅客速度增加到原速度的1.5倍，即1.5y，要想在2小时内使大厅中所有旅客买到票，按这样的安排至少应开售票窗口数为t个，s+2×1.5y=2×tx，解得t=18。

80、有一个93人的参观团，其中男47人，女46人。他们住进一个旅馆内，旅馆内有可住11人、7人、4人的3种房间。要求男、女分住不同房间，且每个房间均住满，至少需要多少房间?_____
A: 11B: 10C: 13D: 17
参考答案: A 本题解释: A 解析： 设男的安排11人房间a间，7人房间b间，4人房间c间。则应满足等式11a+7b+4c=47。在这个等式中，a取尽量大的值a=3，b取最大值2，c取0。因此男的至少安排房间数为3+2+0=5（间）;设女的安排11人房间d间，7人房间e间，4人房间f间，则有11d+7e+4f=46。经试验不难看出，d=1，e=5，f=0。因此女的至少安排房间数为1+5+0=6（间）。总共至少安排房间：5+6=11（间）。故本题选A。

81、商场的自动扶梯以匀速由下往上行驶，两个孩子嫌扶梯走得太慢，于是在行驶的扶梯上，男孩每秒钟向上走2个梯级，女孩每2秒钟向上走3个梯级。结果男孩用40秒钟到达，女孩用50秒钟到达。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 80级 B: 100级 C: 120级 D: 140级
参考答案: B 本题解释:B。【解析】男孩所走的台阶数为40×2=80，女孩所走的台阶数为50/2×3=75，那么电梯的速度就应该为（80-75）/（50-40）=0.5，电梯所经过的台阶就为40×0.5=20， 电梯经过的台阶加上男孩经过的台阶，就是电梯的台阶数，即100级。

82、甲、乙两地相距100千米，张先骑摩托车从甲出发，1小时后李驾驶汽车从甲出发，两人同时到达乙地。摩托车开始速度是50千米/小时，中途减速为40千米/小时。汽车速度是80千米/小时。汽车曾在途中停驶10分钟，那么张驾驶的摩托车减速时是在他出发后的多少小时?_____
A: 1B: 3/2C: 1/3D: 2
参考答案: C 本题解释: C解析：汽车行驶100千米需100÷80=5/4（小时），所以摩托车行驶了5/4+1+1/6=29/12（小时）。如果摩托车一直以40千米/小时的速度行驶，29/12小时可行驶96（2/3）千米，与100千米相差10/3千米。所以一开始用50千米/小时的速度行驶了10/3÷（50-40）=1/3（小时）。故本题选C.

83、甲地到乙地，步行比骑车速度慢75%,骑车比公交慢50%，如果一个人坐公交从甲地到乙地共用1个半小时，问：骑车从甲地到乙地多长时间? _____
A: 10分钟B: 20 分钟C: 30分钟D: 40分钟
参考答案: B 本题解释:B。设骑车的速度为x公里/小时，则步行速度为0.25x公里/小时，公车的速度为2x公里/小时。设甲乙两地距离为L公里，则L/0.25x+L/2x=1.5，得到L/x=1/3小时=20分钟，则骑车从甲地到乙地需20分钟。

84、河道赛道场长120米，水流速度为2米/秒，甲船速度为6米/秒，乙船速度为4米/秒。比赛进行两次往返，甲、乙同时从起点出发，先顺水航行，问多少秒后甲、乙船第二次迎面相遇?_____
A: 48B: 50C: 52D: 54
参考答案: C 本题解释:【答案】C。解析：甲船顺水速度为2+6=8米/秒，逆水速度为6-2=4米/秒;乙船顺水速度为2+4=6米/秒，逆水速度为4-2=2米/秒。

85、已知一杯茶水有若干克，第一次加入一定量的水后，茶水的浓度为6%，第二次又加入同样多的水后，茶水的浓度为4%，求第三次加入同样多的水后茶水的浓度为多少?_____
A: 1%B: 2%C: 3%D: 3.5%
参考答案: C 本题解释:C【解析】设第一次加完水后，含茶6份，含水94份，这样茶水浓度就为6%，第二次加完水后，茶水总量为6÷4%=150份，所以第二次加水为150-100=50份，第三次加入的水也为50份，茶水浓度为6÷（150+50）=0.03=3%。所以，第三次加入同样多的水后茶水的浓度变为3%。故本题正确答案为C。

86、用1，2，3，4，5这五个数字组成没有重复数字的自然数，从小到大顺序排列：1，2，3，4，5，12，……，54321。其中，第206个数是_____
A: 313 B: 12345 C: 325 D: 371
参考答案: B 本题解释:B。由1、2、3、4、5组成的没有重复数字的一位数共有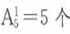；二位数共有个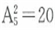；三位数共有个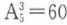；四位数共有个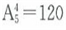；至此由1、2、3、4、5组成的没有重复数字的四位以内的数共有5+20+60+120=205个；那么第206个数是第一个由1、2、3、4、5组成的五位数，即最小的五位数12345。

87、有一个数，除以3余数是2，除以4余数是1。问这个数除以12余数是几?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:B【解析】设这个数除以12，余数是a。那么a除以3，余数是2;a除以4，余数是1。而在0，1，2，…，11中，符合这样条件的a只有5，故这个数除以12余5。

88、某市出租车运费计算方式如下：起步价2公里6元，2公里之后每增加1公里收费1.7元，6公里之后每增加1公里收费2.0元，不足1元按四舍五入计算。某乘客乘坐了31公里，应该付多少元车费？ _____
A: 63 B: 64 C: 65 D: 66
参考答案: A 本题解释:A。2公里以内收费6元；2－6公里收费1.7×4＝6.8元；6－31公里收费2×25＝50元。因此总计应付车费62.8元，四舍五入即63元。故选A项。

89、一个四边形广场，它的四边长分别是60米，72米，84米，96米，现在在四边上植树，四角需种树，而且每两棵树的间隔相等，那么，至少要种多少棵树?_____
A: 22B: 25C: 26D: 30
参考答案: C 本题解释:【解析】C。4个数字都相差12，可将树的间隔设为12米，可种树(60+72+84+96)/12=5+6+7+8=26，选C。

90、幼儿园里，老师将一堆桃子分给同学，如果每个同学分3个则余2个，如果每个同学分4个，则有两个同学分不到，该班有多少个同学?_____
A: 10B: 12C: 15D: 18
参考答案: A 本题解释:A【解析】设共有x个同学，由题意得3x+2=4（x-2），解得x=10。

91、一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是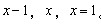。那么有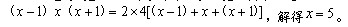所以这个长方体的表面积为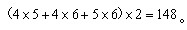

92、今年小方父亲的年龄是小方的3倍，去年小方的父亲比小方大26岁，那么小方明年多大?_____
A: 16B: 13C: 15D: 14
参考答案: D 本题解释:去年小方的父亲比小方大26岁，即年龄差为26。今年小方父亲的年龄是小方的3倍，则年龄差是今年小方年龄的2倍，于是今年小方为13岁，因此明年小方14岁。故选D。

93、若一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞，问大正方体的面积增加了多少? _____
A: 100cm2B: 400cm2C: 500cm2D: 600cm2
参考答案: B 本题解释:B。【解析】正方体6个面，在表面上挖一个边长为10厘米的正方体洞，使得大正方体表面积发生改变：增加的面为正方体洞凹进去的五个面，同时又使大正方体的表面积减少一个正方体洞面面积。因此，大正方体面积最终增加：10*10*5-10*10=400cm2

94、把一根圆木锯成3段需要8分钟，如果把同样的圆木锯成9段需要多少分钟？_____
A: 24分钟B: 27分钟C: 32分钟D: 36分钟
参考答案: C 本题解释:【答案】C。解析：圆木锯成三段有2个切口，2个切口需要用时8分钟，锯成9段有8个切口，则8个切口需要用时8÷2×8＝32（分钟），故正确答案为C。

95、建华中学共有1600名学生，其中喜欢乒乓球的有1180人，喜欢羽毛球的有1360人，喜欢篮球的有1250人，喜欢足球的有1040人，问以上四项球类运动都喜欢的至少有几人？_____
A: 20人B: 30人C: 40人D: 50人
参考答案: B 本题解释:【答案】B。解析：采取逆向思维法。不喜欢乒乓的1600－1180＝420，不喜欢羽毛球的1600－1360＝240，不喜欢篮球的1600－1250＝350，不喜欢足球的1600－1040＝560，要使四项运动都喜欢的人数最少，那么不喜欢的人数就要最多那么都尽量不相交，从而达到最多：420＋240＋350＋560＝1570人，所以喜欢的最少的为1600－1570＝30人，故正确答案为B。

96、某单位有宿舍11间，可以住67人，已知每间小宿舍住5人，中宿舍住7人，大宿舍住8人，则小宿舍间数是_____。
A: 6B: 7C: 8D: 9
参考答案: A 本题解释:【答案】A。解析：设小宿舍有x间，中宿舍有y间，大宿舍有11-x-y间。依题意5x+7y+8（11-x-y）=67，得到3x+y=21。〔化为标准形式〕因为x、y均是大于0的整数，所以x＜7。直接选A。〔确定解的范围〕

97、有甲、乙两汽车站，从甲站到乙站与从乙站到甲站每隔10分同时各发车一辆，且都是1小时到达目的地。问某旅客乘车从甲站到乙站，在途中可看到几辆从乙站开往甲站的汽车?_____
A: 9B: 13C: 14D: 11
参考答案: D 本题解释:D 【解析】某旅客所乘之车在甲站起动时，正好有一辆从乙站开来的车到站停车;同样，当该旅客所乘之车到达乙站时，正好有一辆车从乙站开出，这两辆车均不算该旅客在“途中”看到的，这时，下一辆从乙站开来的汽车离甲站还有10分钟的路程，这辆车与该旅客所乘的车相向而行，相遇时，离甲站有10÷2=5（分钟）的路程。由此可推知，该旅客在途中每隔5分钟就可看到一辆从乙站开往甲站的车。所以从甲站到乙站，该旅客在途中看到60÷5-1=11（辆）从乙站开来的车。

98、学校安排学生住宿，每个房间住6人还有2个空房间，如果每个房间住5人，则有1个房间里住的是3人，问：学校共有（ ）个房间?
A: 8B: 9C: 10D: 11
参考答案: C 本题解释:C【解析】假设学校有学生χ人，有房间y间，所以有6（y-2）=χ，5y-2=χ，由此可以得至χ=48，y=10。

99、从0，1，2，7，9五个数字中任选四个不重复的数字，组成的最大四位数和最小四位数的差是_____。
A: 8442B: 8694　C: 8740D: 9694
参考答案: B 本题解释:答案：B。由题意可得：最大的四位数为9721，最小的四位数为1027，故两者的差是9721-1027=8694。

100、一列快车和一列慢车相对而行，其中快车车长200米，慢车车长250米，坐在慢车上的旅客看到快车驶过其所在窗口的时间是6秒钟，坐在快车上的旅客看到慢车驶过其所在窗口的时间是_____。
A: 6秒B: 6.5秒C: 7秒D: 7.5秒
参考答案: D 本题解释:D【解析】两车相向而行，故慢车、快车相对速度均为V（快）+V（慢），慢车走的路程为快车车长200米;同理，坐在快车上看慢车，走的距离为250米。故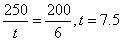。