微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
绝密★启用前
2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)
文科数学
注意事项:
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前考生将自己的姓名、准考证号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷
一、 选择题:本大题共12小题。每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
(1)已知集合M={x|-3<X<1},N={-3,-2,-1,0,1},则M∩N= (A){-2,-1,0,1} (B){-3,-2,-1,0} (C){-2,-1,0} (D){-3,-2,-1 }
(2)|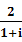 |=
|=
(A)2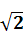 (B)2 (C)
(B)2 (C)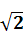 (D)1
(D)1
(3)设x,y满足约束条件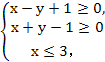 ,则z=2x-3y的最小值是
,则z=2x-3y的最小值是
(A) 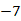 (B)-6 (C)
(B)-6 (C)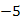 (D)-
(D)-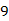
(4)△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=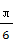 ,C=
,C=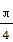 ,则△ABC的面积为
,则△ABC的面积为
(A)2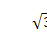
 +2 (B)
+2 (B)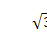 (C)2
(C)2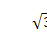 (D)
(D) -1
-1
(5)设椭圆C: 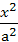 +
+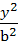 =1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点PF2⊥F1F2,∠PF1F2=30。,则C的离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,P是C上的点PF2⊥F1F2,∠PF1F2=30。,则C的离心率为
(A)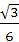 (B)
(B) (C)
(C) (D)
(D)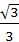
(6)已知sin2α= ,则cos2(α+
,则cos2(α+ )=
)=
 (A)
(A) (B)
(B) (C)
(C) (D)
(D)
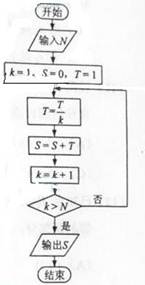
(7)执行右面的程序框图,如果输入的N=4,那么输出的S=
(A)1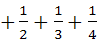
(B)1+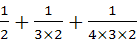
(C)1+ +
+ +
+ +
+
(D)1+ +
+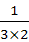 +
+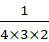 +
+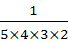
(8)设a=log32,b=log52,c=log23,则
(A)a>c>b (B) b>c>a (C)c>b>a (D)c>a>b
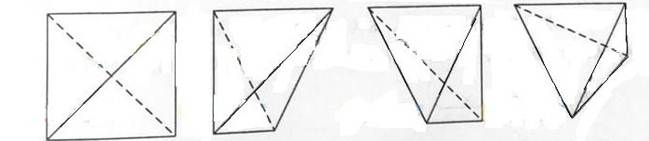 (9)一个四面体的顶点在点间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可为
(9)一个四面体的顶点在点间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可为
(A) (B) (C) (D)
( 10)设抛物线C:y2=4x的焦点为F,直线L过F且与C交于A, B两点.若|AF|=3|BF|,则L的方程为
(A) y=x-1或y=-x+1 (B)y= (X-1)或y=-
(X-1)或y=- (x-1)
(x-1)
(C)y=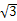 (x-1)或y=-
(x-1)或y=-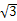 (x-1) (D)y=
(x-1) (D)y=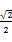 (x-1)或y=-
(x-1)或y=-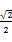 (x-1)
(x-1)
(11)已知函数f(x)=x3+ax2+bx+c ,下列结论中错误的是
(A)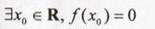
(B)函数y=f(x)的图像是中心对称图形
(C)若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)单调递减
(D)若x0是f(x)的极值点,则f’( x0)=0
(12)若存在正数x使2x(x-a)<1成立,则a 的取值范围是
(A)(-∞,+∞) (B)(-2, +∞) (C)(0, +∞) (D)(-1,+∞)
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题-第21题为必考题,每个试题考生都必须作答。第22题-第24题为选考题,考生根据要求作答。
二.填空题:本大题共4小题,每小题5分。
(13)从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是________.
(14)已知正方形ABCD的边长为2,E为CD的 中点,则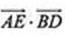 =________.
=________.
(15)已知正四棱锥O-ABCD的体积为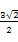 ,底面边长为
,底面边长为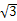 ,则以O为球心,OA为半径的球的表面积为________.
,则以O为球心,OA为半径的球的表面积为________.
(16)函数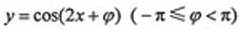 的图像向右平移
的图像向右平移 个单位后,与函数y=sin(2x+
个单位后,与函数y=sin(2x+ )的图像重合,则
)的图像重合,则 =___________.
=___________.
三.解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列。
(Ⅰ)求{an}的通项公式;
(Ⅱ)求a1+a4+a7+…+a3n-2.
(18)(本小题满分12分)
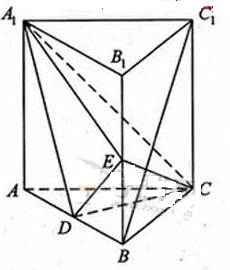
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
(1) 证明: BC1//平面A1CD;
(2) 设AA1= AC=CB=2,AB= ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
(19)(本小题满分12分)
经销商经销某种农产品,在一个销售季度内,每售出It该产品获利润500元,未售
出的产品,每It亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t≤100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将T表示为X的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
(20) (本小题满分12分)
在平面直角坐标系xOy中,己知圆P在x轴上截得线段长为2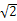 ,在Y轴上截得线
,在Y轴上截得线
段长为2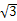 .
.
(Ⅰ)求圆心P的轨迹方程;
(Ⅱ)若P点到直线y=x的距离为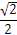 ,求圆P的方程.
,求圆P的方程.
(21)(本小题满分12分)
己知函数f(X) = x2e-x
(I)求f(x)的极小值和极大值;
(II)当曲线y = f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围.
请从下面所给的22,23,24三题中选定一题作答.并用2 B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多涂均按所答第一题评分;多答按所答第一题评分。
(22) (本小题满分10分)选修4-1:几何证明选讲
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D, E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B, E, F,C四点共圆。
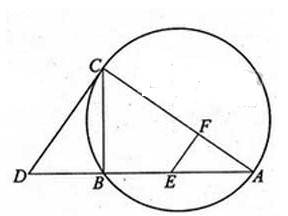
(I) 证明:CA是△ABC外接圆的直径;
(II) 若DB=BE=EA.求过B, E, F,C四点的圆的面积与△ABC外接圆面积的比值.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知动点P. Q都在曲线C: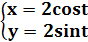 (t为参数)上,对应参数分别为t=a与t=2a(0<a<2π),M为PQ的中点。
(t为参数)上,对应参数分别为t=a与t=2a(0<a<2π),M为PQ的中点。
(I)求M的轨迹的今数方程:
(Ⅱ)将M到坐标原点的距离d表示为a的26数,并判断M的轨迹是否过坐标原点.
(24)(本小题满分10分)选修4-5:不等式选讲
设a,b, c均为正数,且a+b+c=1。证明:
(Ⅰ)ab+bc+ca≤ ;
;
(Ⅱ)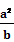 +
+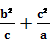 ≥1。
≥1。


