微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2013年普通高等学校招生全国统一考试(天津卷)
文 科 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟. 第Ⅰ卷1至2页, 第Ⅱ卷3至5页.
答卷前, 考生务必将自己的姓名、准考证号填写在答题卡上, 并在规定位置粘贴考试用条形码. 答卷时, 考生务必将答案凃写在答题卡上, 答在试卷上的无效. 考试结束后, 将本试卷和答题卡一并交回.
祝各位考生考试顺利!
第Ⅰ卷
注意事项:
1. 每小题选出答案后, 用铅笔将答题卡上对应题目的答案标号涂黑. 如需改动, 用橡皮擦干净后, 再选凃其他答案标号.
2. 本卷共8小题, 每小题5分, 共40分.
参考公式:
·如果事件A, B互斥, 那么
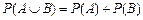
·棱柱的体积公式V = Sh,
其中S表示棱柱的底面面积, h表示棱柱的高.
·如果事件A, B相互独立, 那么
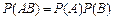
·球的体积公式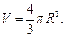
其中R表示球的半径.
一.选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 已知集合A = {x∈R| |x|≤2}, A = {x∈R| x≤1}, 则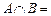
(A) 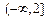 (B) [1,2] (C) [-2,2] (D) [-2,1]
(B) [1,2] (C) [-2,2] (D) [-2,1]
 (2) 设变量x, y满足约束条件
(2) 设变量x, y满足约束条件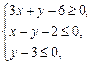 则目标函数z = y-2x的最小值为
则目标函数z = y-2x的最小值为
(A) -7 (B) -4
(C) 1 (D) 2
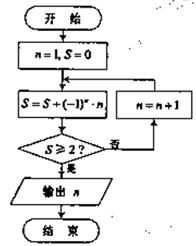
(3) 阅读右边的程序框图, 运行相应的程序, 则输出n的值为
(A) 7 (B) 6
(C) 5 (D) 4
(4) 设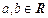 , 则 “
, 则 “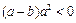 ”是“
”是“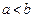 ”的
”的
(A) 充分而不必要条件
(B) 必要而不充分条件
(C) 充要条件
(D) 既不充分也不必要条件
(5) 已知过点P(2,2) 的直线与圆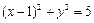 相切, 且与直线
相切, 且与直线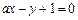 垂直, 则
垂直, 则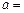
(A) 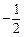 (B) 1
(B) 1
(C) 2 (D) 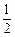
(6) 函数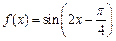 在区间
在区间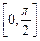 上的最小值是
上的最小值是
(A) 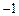 (B)
(B) 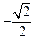
(C) 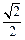 (D) 0
(D) 0
(7) 已知函数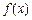 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间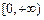 单调递增. 若实数a满足
单调递增. 若实数a满足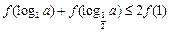 , 则a的取值范围是
, 则a的取值范围是
(A) 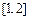 (B)
(B) 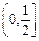
(C) 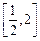 (D)
(D) 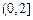
(8) 设函数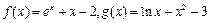 . 若实数a, b满足
. 若实数a, b满足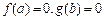 , 则
, 则
(A) 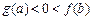 (B)
(B) 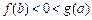
(C) 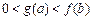 (D)
(D) 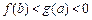
2013年普通高等学校招生全国统一考试(天津卷)
文 科 数 学
第Ⅱ卷
注意事项:
1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上.
2. 本卷共12小题, 共110分.
二.填空题: 本大题共6小题, 每小题5分, 共30分.
(9) i是虚数单位. 复数(3 + i)(1-2i) = .
(10) 已知一个正方体的所有顶点在一个球面上. 若球的体积为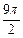 , 则正方体的棱长为 .
, 则正方体的棱长为 .
(11) 已知抛物线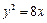 的准线过双曲线
的准线过双曲线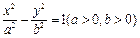 的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .
的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .
(12) 在平行四边形ABCD中, AD = 1, 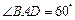 , E为CD的中点. 若
, E为CD的中点. 若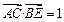 , 则AB的长为 .
, 则AB的长为 .
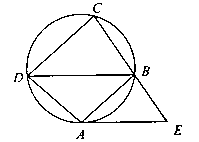 (13) 如图, 在圆内接梯形ABCD中, AB//DC, 过点A作圆的切线与CB的延长线交于点E. 若AB = AD = 5, BE = 4, 则弦BD的长为 .
(13) 如图, 在圆内接梯形ABCD中, AB//DC, 过点A作圆的切线与CB的延长线交于点E. 若AB = AD = 5, BE = 4, 则弦BD的长为 .
(14) 设a + b = 2, b>0, 则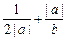 的最小值为 .
的最小值为 .
三.解答题: 本大题共6小题, 共70分. 解答应写出文字说明, 证明过程或演算步骤.
(15) (本小题满分13分)
某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 先从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
|
产品编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
|
质量指标(x, y, z) |
(1,1,2) |
(2,1,1) |
(2,2,2) |
(1,1,1) |
(1,2,1) |
|
产品编号 |
A6 |
A7 |
A8 |
A9 |
A10 |
|
质量指标(x, y, z) |
(1,2,2) |
(2,1,1) |
(2,2,1) |
(1,1,1) |
(2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(⒈) 用产品编号列出所有可能的结果;
(⒉) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
(16) (本小题满分13分)
在△ABC中, 内角A, B, C所对的边分别是a, b, c. 已知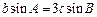 , a = 3,
, a = 3, 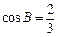 .
.
(Ⅰ) 求b的值;
(Ⅱ) 求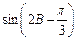 的值.
的值.
 (17) (本小题满分13分)
(17) (本小题满分13分)
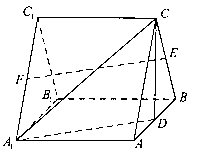
如图, 三棱柱ABC-A1B1C1中, 侧棱A1A⊥底面ABC,且各棱长均相等. D, E, F分别为棱AB, BC, A1C1的中点.
(Ⅰ) 证明EF//平面A1CD;
(Ⅱ) 证明平面A1CD⊥平面A1ABB1;
(Ⅲ) 求直线BC与平面A1CD所成角的正弦值.
(18) (本小题满分13分)
设椭圆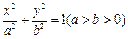 的左焦点为F, 离心率为
的左焦点为F, 离心率为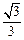 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为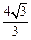 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设A, B分别为椭圆的左右顶点, 过点F且斜率为k的直线与椭圆交于C, D两点. 若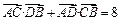 , 求k的值.
, 求k的值.
(19) (本小题满分14分)
已知首项为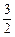 的等比数列
的等比数列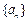 的前n项和为
的前n项和为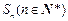 , 且
, 且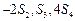 成等差数列.
成等差数列.
(Ⅰ) 求数列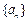 的通项公式;
的通项公式;
(Ⅱ) 证明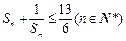 .
.
(20) (本小题满分14分)
设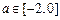 , 已知函数
, 已知函数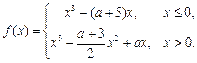
(Ⅰ) 证明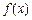 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
(Ⅱ) 设曲线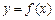 在点
在点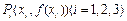 处的切线相互平行, 且
处的切线相互平行, 且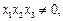 证明
证明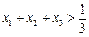 .
.