高考物理知识大全《匀变速直线运动》高频考点巩固（2017年模拟版） - 高考物理题库

高考物理知识大全《匀变速直线运动》高频考点巩固（2017年模拟版）(十)

2017-08-22 01:44:36 来源:91考试网作者:www.91exam.org 【大中小】

微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!

1、选择题做匀减速直线运动的物体，它的加速度大小为a，初速度大小是v0，经过时间t速度减小到零，则它在这段时间内的位移大小表达错误的是（　　）
A．v0t+

1
2

at2
B．v0t-

1
2

at2
C．

v0
2

t
D．

1
2

at2

参考答案：A、B由题意，初速度为v0，加速度大小为a，时间为t，加速度为-a，则匀减速运动的位移为：s=v0t-12at2，故A错误，B正确．
C、由题，物体做匀减速直线运动，已知初速度为v0，末速度为0，则平均速度为.v=v0+02=v02
所以这段时间内物体的位移 s=.vt=v02t，故C正确．
D、此运动可看出反向的初速度为零的匀加速运动，则 s=12at2，故D正确．
本题选错误的
故选：A

本题解析：

本题难度：一般

2、简答题如图所示，水平地面上质量为M=3kg的物块，在大小为F=16N、方向与水平方向成θ=37°的拉力作用下沿地面向右作匀加速直线运动．若木块与地面之间的动摩擦因数为μ=

1
3

，（g=10m/s2，sin37°=0.6，cos37°=0.8）求：
（1）木块的加速度大小．
（2）若不改变拉力的方向，只改变拉力的大小，求出物体沿水平地面做匀加速直线运动，拉力大小与木块加速度的函数表达式．（设木块与地面间的最大静摩擦力等于它们之间的滑动摩擦力）
（3）求上述条件下拉力的取值范围，并以拉力大小为纵坐标，以木块的加速度为横坐标，在坐标系作出它们的图象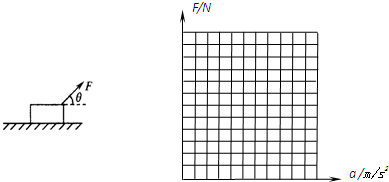． 91考试网

参考答案：
91考试网
（1）根据牛顿第二定律得：
Fcosα-μ（mg-Fsinα）=ma?
则a=F(cosα+μsinα)m-μg=2m/s2
（2）由F=m(μg+a)cosα+μsinα，得：
F=3×(13×10+a)0.8+13×0.6=3a+10．
（3）当a=0，Fmin=10N
当N=0时，有Fsinθ=G=mg，Fmax=50N
如图．
答：（1）木块的加速度大小为2m/s2．
（2）拉力大小与木块加速度的函数表达式为F=3a+10．
（3）拉力的大小范围为[10N，50N]，图线如图．

本题解析：

本题难度：一般

3、选择题一个物体从静止开始做匀变速直线运动，下面有三种说法，正确的是
①第1s内、前2s内、前3s内…相应的运动距离之比一定是x1∶x2∶x3∶…＝1∶4∶9∶…
②第1s内、第2s内、第3s内…相邻的相同时间内的位移之比一定是xⅠ∶xⅡ∶xⅢ∶… ＝1∶3∶5∶…
③相邻的相同时间内位移之差值一定是Δx＝aT2，其中T为相同的时间间隔
[? ]
A．只有③正确　　　　　
B．只有②③正确
C．都是不正确的
D．都是正确的

参考答案：D

本题解析：

本题难度：简单

4、计算题升降机以速度v=4.9 m/s匀速竖直上升，升降机内的天花板上有一个螺丝帽突然松脱，脱离天花板。已知升降机天花板到其地板的高度为h=14.7 m。求螺丝帽落到升降机地板所需时间。

参考答案：解：上升过程：螺丝帽脱离升降机后以v=4.9 m／s的初速度竖直向上运动
上升到最高点时间：t1=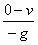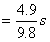0.5 s
上升到最高点的位移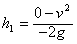：=1.225 m
螺丝帽的运动过程如图所示，由图中位移约束关系得

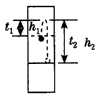
h1+h=h2+v(t1+t2)，即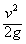+h=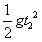+v(t1+t2)
代入数据化简得：t22+t2-2.75=0
解得：t2≈1.23 s
因此，螺丝帽落到地板所需时间t=t1+t2=1.73 s