1、选择题  某人把原来静止于地面上的质量为2kg的物体向上提1m，并使物体获得1m/s的速度，取g为10m/s2，则这过程中正确的是（　　）
A．人对物体做功21J
B．合外力对物体做功1J
C．合外力对物体做功21J
D．物体重力势能增加21J

参考答案：A、设人对物体做功为W，根据动能定理得，W-mgh=12mv2，代入解得W=21J．故A正确．
? B、C根据动能定理得，合外力做功W合=12mv2=1J．故B正确，C错误．
? D、物体向上运动的过程中，重力做负功，为WG=-mgh=-20J，则物体重力势能增加20J．故D错误．
故选AB

本题解析：

本题难度：一般

2、简答题  光滑水平面上放有如图所示的用绝缘材料制成的“┙”型滑板，（平面部分足够长），质量为4m，距滑板的A壁为L1距离的B处放有一质量为m，电量为+q的大小不计的小物体，物体与板面的摩擦不计，整个装置处于场强为E的匀强电场中，初始时刻，滑板与物体都静止，试求：
（1）释放小物体，第一次与滑板A壁碰前物体的速度v1多大？
（2）若物体与A壁碰后相对水平面的速度大小为碰前的

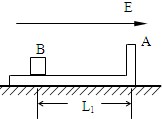
参考答案：（1）由动能定理得 qEL1=12mv21 得 v1=

本题解析：

本题难度：一般

3、简答题  在如图所示的电路中，两平行正对金属板A、B水平放置，两板间的距离d=4.0cm．电源电动势E=400V，内电阻r=20Ω，电阻R1=1980Ω．闭合开关S，待电路稳定后，将一带正电的小球（可视为质点）从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间，小球恰好能到达A板．若小球所带电荷量q=1.0×10-7C，质量m=2.0×10-4kg，不考虑空气阻力，忽略射入小球对电路的影响，取g=10m/s2．求：
（1）A、B两金属板间的电压的大小U；
（2）滑动变阻器消耗的电功率P滑；
（3）电源的效率η．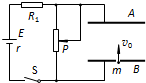

参考答案：（1）小球从B板上的小孔射入恰好到达A板的过程中，在电场力和重力的作用下做匀减速直线运动，设A、B两极板间电压为U，根据动能定理有
-qU-mgd=0-12mv02
解得U=200V
（2）设此时滑动变阻器接入电路中的电阻值为R滑，根据闭合电 路欧姆定律可知，电路中的电流
得 I=ER1+R滑+r
根据部分电路欧姆定律可知? U=IR滑
解得? R滑=2.0×103Ω
滑动变阻器消耗的电功率? P滑=U2R滑=20W
?（3）电源的效率η=P出P总=I2(R1+R滑)I2(R1+R滑+r)=99.5%
答：
（1）A、B两金属板间的电压的大小U是200V；
（2）滑动变阻器消耗的电功率P滑是2.0×103Ω．
（3）电源的效率η是99.5%．

本题解析：

本题难度：一般

4、填空题  质量M=1kg的物体，在水平拉力F的作用下，沿粗糙水平面运动，至位移为4m处，拉力F停止作用，至位移为8m处物体停止运动，运动过程中的Ek-s图线如图所示．物体的初速度为______m/s，物体和水平面间的滑动摩擦因数为______，拉力F的大小为______N．（g取10m/s2）

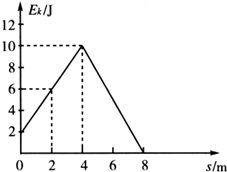
参考答案：（1）从图线可知初动能为2J，Ek0=12mv2=2J，
解得v=2m/s．
（2）在位移4m处物体的动能为10J，在位移8m处物体的动能为零，这段过程中物体克服摩擦力做功．
设摩擦力为Ff，则-Ffx2=0-10J=-10J，Ff=N=2.5N，因Ff=μmg
故μ=0.25．
（3）物体从开始到移动4m这段过程中，受拉力F和摩擦力Ff的作用，合力为F-Ff，
由动能定理得：（F-Ff）?x1=△Ek，
故得F=4.5N．
故答案为：2；0.25；4.5．

本题解析：

本题难度：一般

5、计算题  如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强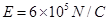，方向水平向左。带电的物块B静止在电场边缘的O点，带电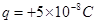量、质量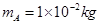的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍，A、B与地面间的动摩擦因数都为=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。

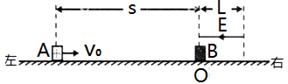
(1) 求A到达O点与B碰撞前的速度大小；
(2) 求碰撞后瞬间A和B的速度大小；
(3) 讨论K在不同取值范围时电场力对A做的功。

参考答案：(1) 4m/s? (2)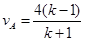m/s 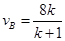?m/s? (3)（i）当k＞3时A能从电场右边界离开电场力对A做功为1.2×10-2 J；在1＜k≤3范围内，A从电场的左侧离开，整个过程电场力做功为0。

本题解析：（1）设碰撞前A的速度为v，由动能定理
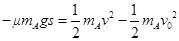?①
得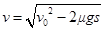： =4m/s?②
（2）设碰撞后A、B速度分别为vA、vB，且设向右为正方向；由于弹性碰撞，所以有：
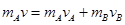?③
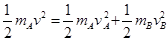?④
联立③④并将mA=kmB及v=4m/s代入得：
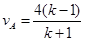m/s?⑤
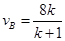?m/s?⑥
（3）讨论：
（i）如果A能从电场右边界离开，必须满足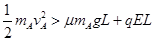：?⑦
联立⑤⑦代入数据，得： k＞3?⑧
电场力对A做功为：WE=-qEL=-6×105×5×10-8×0.4(J)=-1.2×10-2(J)?⑨
（ii）如果A不能从电场右边界离开电场，必须满足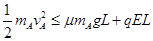：?⑩
联立⑤⑩代入数据，得：k≤3?
考虑到k＞1，所以在1＜k≤3范围内A不能从电场右边界离开?
又：? qE=3×10-2N＞μmg=2×10-2N?
所以A会返回并从电场的左侧离开，整个过程电场力做功为0．即：WE=0?

本题难度：一般