微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图所示,空间存在相互垂直的匀强电场 和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是
和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是
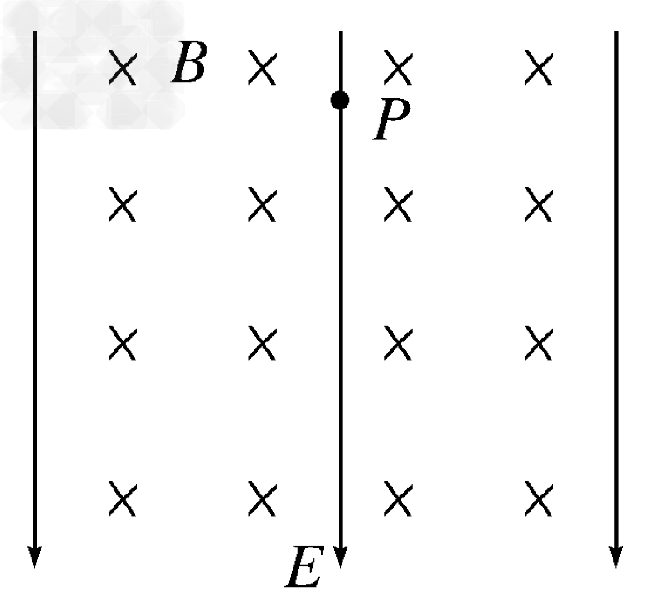
[? ]
A.若仅撤去电场,P可能做匀加速直线运动
B.若仅撤去磁场,P可能做匀速直线运动
C.若给P一初速度,P不可能做匀速直线运动
D.若给P一初速度,P可能做匀速圆周运动
参考答案:BD
本题解析:
本题难度:一般
2、选择题 如图甲所示,在一条电场线上有A、B两点,若从A点由静止释放一电子,假设电子仅受电场力作用,电子从A点运动到B点的速度-时间图像如图乙所示,则(?)
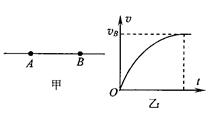
A. 电子在A、B两点受的电场力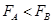 ?
?
B.A、B两点的电场强度相同
C.A、B两点的电势
D.电子在A、B两点具有的电势能
参考答案:C
本题解析:由v-t图像知,图线的斜率减小,则电子运动的加速度减小,由F=ma知电场力减小,即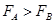 ,A错;由
,A错;由 知场强减小,B错;因电子做加速运动,所以电场力是从A到B,场强方向为从B到A,因沿电场线方向电势降低,所以
知场强减小,B错;因电子做加速运动,所以电场力是从A到B,场强方向为从B到A,因沿电场线方向电势降低,所以 ,C对;因电子做加速运动,所以电场力做正功,电势能减小,即
,C对;因电子做加速运动,所以电场力做正功,电势能减小,即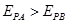 ,D错。
,D错。
点评:本题学生能从v-t图像判断出电子做加速度减小的加速运动,且电场力做正功。
本题难度:一般
3、计算题 在足够大的绝缘光滑水平面上有一质量m=1.0×10-3kg、带电量q=1.0×10-10C的带正电的小球,静止在O点.以O点为原点,在该水平面内建立直角坐标系xOy.在t0=0时突然加一沿x轴正方向、大小E1=2.0×106V/m的匀强电场,使小球开始运动.在t1=1.0s时,所加的电场突然变为沿y轴正方向、大小E2=2.0×106V/m的匀强电场.在t2=2.0s时所加电场又突然变为另一个匀强电场E3,使小球在此电场作用下在t3=4.0s时速度变为零.求:
(1)在t1=1.0s时小球的速度v1的大小;
(2)在t2=2.0s时小球的位置坐标x2、y2;
(3)匀强电场E3的大小;
参考答案:(1) 0.2m/s (2) 0.3m 0.1m (3) E3=1.4×106V/m
本题解析:(1)0~1s对小球应用牛顿第二定律得:
qE1=ma1
解得小球的加速度为:a1=qE1/m=0.2m/s2
小球在t1=1.0s时的速度大小为:
v1=a1t1=0.2×1m/s=0.2m/s
(2)小球在t1=1.0s时的位置坐标为:
x1=a1t=×0.2×1.02m=0.1m
在1.0s~2.0s内对小球应用牛顿第二定律得:qE2=ma2
解得小球的加速度为:a2=qE2/m=0.2m/s2
在t2=2.0s时小球的位置坐标为:
x2=x1+v1(t2-t1)=0.1m+0.2×1.0m=0.3m
y2=a2(t2-t1)2=×0.2×1.02m=0.1m
设在t2=2.0s时小球的速度为v2,则有:
v=v+(at2)2
解得:v2=v1=×0.2m/s=0.28m/s
(3)2.0s~0.4s内对小球应用牛顿第二定律得:
qE3=ma3
小球在4.0s时速度减为零,说明小球做匀减速直线运动,由运动学公式得:
v4=v2-a3t3
联立解得匀强电场E3的大小为:
E3=1.4×106V/m
点评:本题的过程比较多,涉及的物理量很多,所以在计算时一定要细心,难度不大,
本题难度:一般
4、选择题 如图所示,带负电的液滴以速度v垂直射入方向一致的水平匀强磁场和匀强电场区域,则液滴可能做(?)
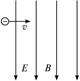
A.匀速直线运动
B.匀变速直线运动
C.匀变速曲线运动
D.匀速圆周运动
参考答案:C
本题解析:此题极易错选为D,原因是将场区当成竖直向下的,未看清题目中同向场区是水平的.显然A、B、D不可能.当mg=qvB时,带电粒子受合外力为qE.且初速v与qE互相垂直,在初速v方向液滴做匀速直线运动,在电场力qE方向做初速为零的匀加速直线运动(此方向分速度与磁场方向平行,不会引起液滴所受洛伦兹力的变化).
故液滴虽然速率增大,但合外力仍然恒定,所以液滴是可能做匀变速曲线运动的,正确选项为C.
本题难度:简单
5、计算题 (14分)如图所示,两根足够长的平行光滑金属导轨MN、PQ与水平面的夹角为a=30°,导轨电阻不计,导轨处在垂直导轨平面斜向上的有界匀强磁场中. 两根电阻都为R=2W、质量都为m=0.2kg的完全相同的细金属棒ab和cd垂直导轨并排靠紧的放置在导轨上,与磁场上边界距离为x=1.6m,有界匀强磁场宽度为3x=4.8m.先将金属棒ab由静止释放,金属棒ab刚进入磁场就恰好做匀速运动,此时立即由静止释放金属棒cd,金属棒cd在出磁场前已做匀速运动.两金属棒在下滑过程中与导轨接触始终良好(取重力加速度g=10m/s2).求:

(1)金属棒ab刚进入磁场时棒中电流I;
(2)金属棒cd在磁场中运动的过程中通过回路某一截面的电量q;
(3)两根金属棒全部通过磁场的过程中回路产生的焦耳热Q.
参考答案:(1) I=1A (2)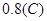 ?(3) 8J
?(3) 8J
本题解析:(1)mgxsina=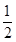 mv12,?v1=
mv12,?v1=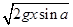 =4m/s(1分)
=4m/s(1分)
 =mgsina,BL=1Tm(1分)
=mgsina,BL=1Tm(1分)
BIL=mgsina,I=1A?(1分)
(2)设经过时间t1,金属棒cd也进入磁场,其速度也为v1,金属棒cd在磁场外有x=v1/2·t1,此时金属棒ab在磁场中的运动距离为:X=v1t1=2x,?
两棒都在磁场中时速度相同,无电流,金属棒cd在磁场中而金属棒ab已在磁场外时,cd棒中才有电流,运动距离为2x(得到cd棒单独在磁场中运动距离为2x,即可得2分)
 (公式2分、结果1分)
(公式2分、结果1分)
(3)金属棒ab在磁场中(金属棒cd在磁场外)回路产生的焦耳热为:
Q1=mgsina?2x=3.2J (或:Q1=2I2Rt1=mgsina?2x)(1分)
金属棒ab、金属棒cd都在磁场中运动时,回路不产生焦耳热。两棒加速度均为gsina,ab离开磁场时速度为v 2,v22-v12=2gxsina,v2= 。(1分)
。(1分)
金属棒cd在磁场中(金属棒ab在磁场外),金属棒cd的初速度为v2= ,末速度为
,末速度为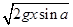 ,由动能定理:
,由动能定理:
mgsina?2x-Q2=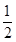 m(
m(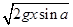 )2-
)2-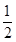 m(
m( )2(2分)
)2(2分)
Q2=mgsina?3x=4.8J(1分)
Q=mgsina?5x=8J(1分)
点评:在分析导体棒切割磁感线运动问题时,需要结合受力分析, 特别是把握好题目的临界条件,比如什么时候匀速运动,
本题难度:一般