1、填空题  质量为 10 kg的环在F＝200 N的拉力作用下，沿粗糙直杆由静止开始运动，杆与水平地面的夹角θ＝37°，拉力F与杆的夹角也为θ。力F作用0.5s后撤去，环在杆上继续上滑了0.4s后，速度减为零。（已知sin37°＝0.6，cos37°＝0.8，g＝10 m/s2）求：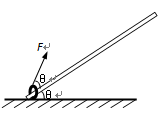
小题1:环与杆之间的动摩擦因数μ=??；
小题2:环沿杆向上运动的总距离s=?m。

参考答案：
小题1:0.5
小题2:1.8

本题解析：分析：（1）环先沿杆做匀加速直线运动，后做匀减速直线运动．由题两个过程时间已知，根据运动学公式求出两段过程加速度关系．根据牛顿第二定律分别得到加速度的表达式，再联立求解μ．
（2）由位移公式分别求出两个过程的位移，位移之和等于环沿杆向上运动的总距离s．
解答：解：（1）设环做匀加速直线运动和匀减速直线运动的加速度大小分别为a1和a2，撤去力F瞬间物体的速度为v，
则由?v=a1t1和?0=v-a2t2
得a1t1=a2t2?代入得2a1=1.6a2①
根据牛顿第二定律得
Fcosθ-mgsinθ-μ（Fsinθ-mgcosθ）=ma1?②
mgsinθ+μmgcosθ=ma2?③
由①，②，③式联立解得?μ=0.5
（2）将μ=0.5代入②，③得
a1=8m/s2，a2=10m/s2
所以环沿杆向上运动的总距离s=a1t12+a2t22=（×8×0.52+×10×0.42）m=1.8m．
答：（1）环与杆之间的动摩擦因数μ=0.5；
（2）环沿杆向上运动的总距离s=1.8m．
点评：本题应用牛顿第二定律和运动学规律结合处理动力学问题，第（1）问也可以用动量定理求解μ．

本题难度：简单

2、选择题  如图所示，一重为10 N的球固定在支杆AB的上端，今用一段绳子水平拉球，使杆发生弯曲，已知绳的拉力为7.5N，则AB杆对球的作用力

[? ]
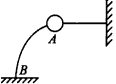
A.大小为7.5 N
B.大小为10N
C.方向与水平方向成53°角斜向右下方
D.方向与水平方向成53°角斜向左上方

参考答案：D

本题解析：

本题难度：简单

3、选择题 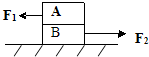 如图所示，AB两物体受到水平向左F1=10N，水平向右F2=20N的力的作用，但都保持静止，则A物体受到的摩擦力f1和地面对B的摩擦力f2大小、方向分别为
A.f1=10N?向左，f2=10N?向右
B.f1=10N?向右，f2=10N?向右
C.f1=10N?向左，f2=10N?向左
D.f1=10N?向右，f2=10N?向左

参考答案：D

本题解析：分析：对整体受力分析，通过共点力平衡，求出地面对B的摩擦力，隔离对A分析，得出B对A的摩擦力大小．
解答：整体在水平方向上受力平衡，由于F2＞F1，知整体在水平方向上受两个拉力以及地面对B的摩擦力，有：F1+f2=F2，所以地面对B的摩擦力f2=10N，方向向左．
对A分析，A在水平方向上拉力F1和B对A的静摩擦力，两个力平衡，所以f1=F1=10N，方向向右．故D正确，A、B、C错误．
故选D．
点评：解决本题的关键能够正确地受力分析，运用共点力平衡求解，注意整体法和隔离法的运用．

本题难度：一般

4、计算题  一质量不计的弹簧原长为10 cm，一端固定于质量m＝2 kg的物体上，另一端施一水平拉力F。( g=10m/s2，设最大静摩擦力与滑动摩擦力相等)
(1)若物体与水平面间的动摩擦因数为0.2，当弹簧拉长至14cm时，物体恰好被拉动，弹簧的劲度系数多大？
(2)若将弹簧拉长至11 cm时（物体在滑动过程中），物体所受的摩擦力大小为多少？
(3)物体静止时，若将弹簧拉长至13cm，物体所受到的摩擦力大小为多少？

参考答案：（1）4N（2）4N（3）3N

本题解析：（1）由题意得，物体与地面间最大静摩擦力为：
?（2分）
物体恰好被拉动，物体所受弹力等于最大静摩擦力：得:
?　　　 ?(3分)
物体相对地面滑动，受到滑动摩擦力：
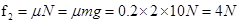　　　　　　　　? (2分)
（3）弹簧弹力?（3分）
点评：静摩擦力与滑动摩擦力要根据物体的状态确定，注意静摩擦力不能由f=μN求解，只能根据平衡条件或牛顿定律求解．

本题难度：一般

5、简答题  一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°．求两小球的质量之比

参考答案：对质量为m2的物体受力分析：受重力和拉力，由平衡条件得：绳上的拉力大小T=m2g
对质量为m1的物体受力分析并合成如图：由平衡条件得：F′=m1g

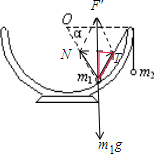
因为角α是60°，所以三角形为等边三角形，画出来的平行四边形为菱形．
连接菱形对角线，对角线相互垂直，红色三角形为直角三角形：
由三角函数关系：
sinα=F′2T=m1′g2T=m1g2m2g
由α=60°得：m1g2m2g=

本题解析：

本题难度：一般