1、计算题  如图所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感应强度相同的匀强磁场，方向垂直纸面向外，ab是一根长为L的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上.将一套在杆上的带正电的小球从a端由静止释放后，小球先做加速运动，后做匀速运动到达b端.已知小球与绝缘杆间的动摩擦因数μ=0.3，小球重力忽略不计，当小球脱离杆进入虚线下方后，运动轨迹是半圆，圆的半径是L/3，求带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值.

参考答案：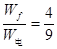

本题解析：小球在沿杆向下运动时，受力情况如图所示:

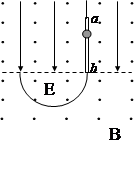
在水平方向:N="qvB" ，所以摩擦力f=μN=μqvB
当小球做匀速运动时：qE=f=μqvbB? (2分)
小球在磁场中做匀速圆周运动时，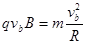
又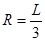，所以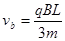? (4分)
小球从a运动到b的过程中，由动能定理得：
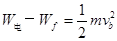?（2分）
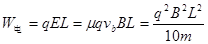而?（2分）
所以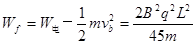
则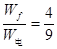? (2分)

本题难度：一般

2、实验题  如图所示，在直角坐标系O-xyz中存在磁感应强度为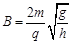、方向竖直向下的匀强磁场，在（0，0，h）处固定一电量为+q（q>0）的点电荷，在xOy平面内有一质量为m(m未知),电量为-q的微粒绕原点O沿图示方向作匀速圆周运动。若微粒的圆周运动可以等效为环形电流，求：

（1）若已知+q与-q的连线与z轴的夹角θ和静电力常量k,则此微粒所受的库仑力多大
（2）此微粒作匀速圆周运动的角速度ω；
（3）等效环形电流的电流强度I（已知重力加速度为g）。

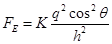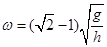参考答案：（1）（2）（3）

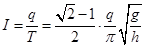
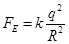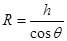本题解析：（1）(6分)该微粒受到的库仑力FE: (2分)， (2分)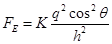，? (2分)。

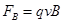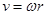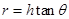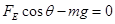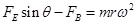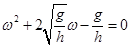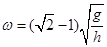（2）(8分)，，由几何关系 ?(2分)，微粒沿在z轴方向上受力平衡 ?(2分)，微粒在xoy平面内做圆周运动 ?(2分)，联立，解得 ，解得 (2分)，
（3）(5分)微粒圆周运动的周期 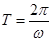(2分)，等效电流强度 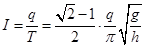?(3分)

本题难度：简单

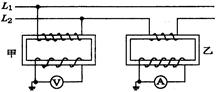
3、选择题  如图所示，L1和L2是输电线，甲是电压互感器，乙是电流互感器。若已知甲的变压比为1000：1，乙的变流比为100：l，并且已知加在电压表两端的电压为220V，通过电流表的电流为10A，则输电线的输送功率为（?）?

A．2.2×103W　　　
B．2.2×10-2W　　　
C．2.2×l08W　　
D．2.2×104W

参考答案：C

本题解析：依题输送电压为2.2×l05V，输送电流为1×103V

本题难度：简单

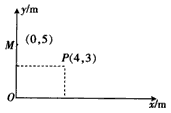
4、计算题  xOy平面为一光滑水平面，在x>0、y>0的空间区域内有平行于xOy平面的匀强电场，场强大小为100 V/m；在x>0、y＜3 m的区域内同时有垂直于xOy平面的磁场。一质量m=10-6 kg、电荷量q=2×10-7 C的带负电粒子从坐标原点O以一定的初动能入射，在电场和磁场的作用下发生偏转，到达(4，3)点时，动能变为初动能的0.2倍，速度方向平行于y轴正方向。最后，粒子从y轴上y=5 m的M点射出电场，动能变为初动能的0.52倍，求：
(1)OP连线上与M点等电势的点的坐标。
(2)粒子由P点运动到M点所需的时间。

参考答案：解：(1)设粒子在P点时的动能为Ek，则初动能为5Ek，在M点的动能为2.6Ek。由于洛伦兹力不做功，粒子从O点到P点和从P点到M点的过程中，电场力做的功分别为一4Ek和1.6Ek，O点和P点及M点的电势差分别为：


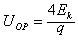
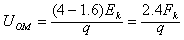
由几何关系得OP的长度为5m，沿OP方向电势每米下降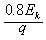。设OP连线上与M点电势相等的点为D，则：OD=3 m
OP与x轴的夹角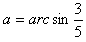
D点的坐标为xD=3cosα=2.4 m，YD=3sinα=1.8 m
(2)过P点作PN垂直于x轴，N为垂足，由几何关系可得△MOD与△PON全等，故MD⊥OP。电场方向与等势线MD垂直，即电场沿OP方向

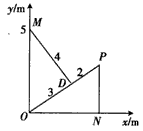
设粒子在P点的速度大小为v，在由O点运动到P点的过程中满足qE·OP=4Ek=2mv2
粒子在由P运动到M的过程中，在垂直电场方向不受外力，做匀速直线运动，其速度大小为：v⊥=vcosα
运动的距离s=4 m

本题解析：

本题难度：困难

5、计算题  如图所示，质量M=0.01kg的导体棒ab，垂直放在相距l=0.1m的平行光滑金属导轨上。导轨平面与水平面的夹角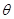=30°，并处于磁感应强度大小B=5T、方向垂直于导轨平面向下的匀强磁场中。左侧是水平放置的平行金属板，它的极板长s=0.1m，板间距离d=0.01m。定值电阻R=2Ω，Rx为滑动变阻器的阻值，不计其它电阻。

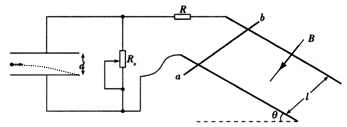
（1）调节Rx＝2Ω，释放导体棒，当棒沿导轨匀速下滑时，求通过棒的电流I及棒的速率v
（2）改变Rx ，待棒沿导轨再次匀速下滑后，将质量m=10-8kg、电量q=10-4C的带正电的粒子从两金属板中央左侧以v0=103 m/s水平射入，（不计粒子的重力），若它恰能从下板右边缘射出，求此时的Rx.

参考答案：（1）0.1A，0.8m/s（2）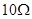

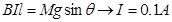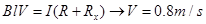本题解析：（1）根据受力分析可得：?（３分）
　　　（３分）
（２）根据牛顿第二定律可得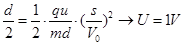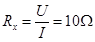：　。（３分）
点评：由电磁感应定律求电动势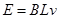、闭合电路欧姆定律求电流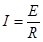，由导体棒受力平衡求速度，由带电粒子的匀速通过电容器求电压，结合闭合电路求速度．

本题难度：简单