微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、计算题 (18分)如图所示,k是产生带电粒子的装置,从其小孔a水平向左射出比荷为1.0×l03C/kg的不同速率的带电粒子,带电粒子的重力忽略不计.Q是速度选择器,其内有垂直纸面向里的磁感应强度为3.0×l0-3T的匀强磁场和竖直方向的匀强电场(电场线未画出).
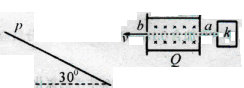
(1)测得从Q的b孔水平向左射出的带电粒子的速率为2.0×l03m/s,求Q内匀强电场场强的大小和方向.
(2)为了使从b孔射出的带电粒子垂直地打在与水平面成30°角的P屏上,可以在b孔与P屏之间加一个边界为正三角形的有界匀强磁场,磁场方向垂直纸面.试求该正三角形匀强磁场的最小面积S与磁感应强度B间所满足的关系.
参考答案:解:(1)从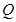 的
的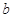 孔水平向左射出的速率为
孔水平向左射出的速率为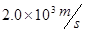 的带电粒子一定在
的带电粒子一定在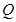 中做匀速直线运动,由平衡条件得:
中做匀速直线运动,由平衡条件得: ?(1)2分
?(1)2分
可得: ?(2)2分
?(2)2分
由分析判断可知, 的方向竖直向上。?(3)2分
的方向竖直向上。?(3)2分
(2)设带电粒子从 点进入磁场,从
点进入磁场,从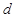 点射出磁场,带电粒子在磁场中运动的轨迹如图所示。由图可得,
点射出磁场,带电粒子在磁场中运动的轨迹如图所示。由图可得,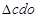 是正三角形,
是正三角形,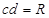 ?(4)2分
?(4)2分
由分析可知,将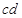 作为正三角形匀强磁场的一个边界时,正三角形匀强磁场的面积最小,所以该正三角形匀强磁场的区域如图中
作为正三角形匀强磁场的一个边界时,正三角形匀强磁场的面积最小,所以该正三角形匀强磁场的区域如图中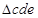 区域。?(5)2分
区域。?(5)2分
由于边长为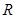 的正三角形
的正三角形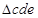 的高为
的高为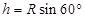 ?(6)2分
?(6)2分
边长为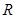 的正三角形
的正三角形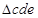 的面积为
的面积为 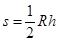 ?(7)2分
?(7)2分
又带电粒子做匀速圆周运动的轨道半径为 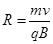 ?(8)2分
?(8)2分
由(6)、(7)、(8)解得,正三角形匀强磁场的最小面积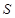 与磁感应强度
与磁感应强度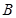 间所满足的关系:
间所满足的关系:
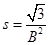 ?(9)2分
?(9)2分
本题解析:略
本题难度:一般
2、计算题 (12分)如图所示,处于匀强磁场中的两根足够长。电阻不计的平行金属导轨相距1m,导轨平面与水平面成370角,下端连接阻值为R的电阻。匀强磁场方向与导轨平面垂直。质量为0.2kg。电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25。求:

(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻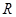 消耗的功率为
消耗的功率为 ,求该速度的大小;
,求该速度的大小;
(3)在上问中,若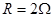 ,金属棒中的电流方向
,金属棒中的电流方向 到
到 ,求磁感应强度的大小与方向。(
,求磁感应强度的大小与方向。(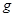 取
取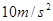 ?,
?,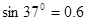 ,
, )
)
参考答案:(1)4m/s2?(2)10m/s? (3)0.4T, 磁场方向垂直导轨平面向上
本题解析:(1)金属棒开始下滑的初速为零,没有感应电流产生,不受安培力作用,故根据牛顿第二定律有:mgsinθ-μmgcosθ=ma?①
由①式解得a=10×(O.6-0.25×0.8)m/s2=4m/s2?②
(2)设金属棒运动达到稳定时,做匀速运动,速度为v,所受安培力为F,棒在沿导轨方向受力平衡,则有:mgsinθ一μmgcosθ一F=0 解得 F=0.8N?③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率Fv=P?④
由③、④两式解得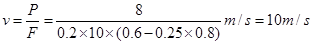 ?⑤
?⑤
(3)设电路中电流为I,两导轨间金属棒的长为l,磁场的磁感应强度为B
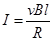 ?⑥
?⑥
P=I2R?⑦
由⑥、⑦两式解得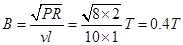 ?⑧
?⑧
由左手定则可知,磁场方向垂直导轨平面向上
本题难度:一般
3、计算题 如图所示,串联阻值为R的闭合电路中,面积为S的正方形区域abcd存在一个方向垂直纸面向外、磁感应强度均匀增加且变化率为k的匀强磁场Bt,abcd的电阻值也为R,其他电阻不计。电阻两端又向右并联一个平行板电容器。在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为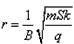 。求:
。求:
(1)电容器获得的电压;
(2)带电粒子从小孔P射入匀强磁场时的速度;
(3)带电粒子在圆形磁场运动时的轨道半径及它离开磁场时的偏转角。
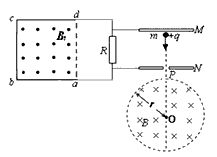
参考答案:解:(1)根据法拉第电磁感应定律,闭合电路的电动势为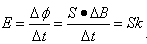
根据闭合电路的欧姆定律,闭合电路的电流为
电阻获得的电压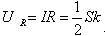
因电容器与电阻是并联的,故电容器获得的电压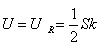
(2)带电粒子在电容器中受到电场力作用而做匀加速直线运动,根据动能定理,有: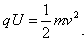
得到带电粒子从小孔射入匀强磁场时的速度为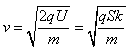
(3)带电粒子进入圆形匀强磁场后,洛伦兹力提供其做匀速圆周运动的向心力,有: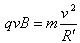
得带电粒子在圆形匀强磁场运动的半径为
又圆形磁场的半径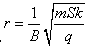 ,即
,即
根据左手定则,带电粒子在圆形磁场向右转过的圆周(如右图所示),故它离开磁场时的偏转角为90°。
本题解析:
本题难度:困难
4、选择题 (2011年泉州高三统考)如图8-3-18所示,匀强电场和匀强磁场相互垂直,现有一束带电粒子(不计重力),以速度v0沿图示方向恰能直线穿过,则以下分析不正确的是( )
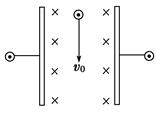
图8-3-18
A.如果让平行板电容器左极为正极,则带电粒子必须向上以v0进入该区域才能直线穿过
B.如果带电粒子以小于v0的速度沿v0方向射入该区域,其电势能越来越小
C.如果带负电粒子速度小于v0,仍沿v0方向射入该区域,其电势能越来越大
D.无论带正电还是带负电的粒子,若从下向上以速度v0进入该区域时,其动能都一定增加
参考答案:C
本题解析:选C.带电粒子做直线运动,必有Eq=qvB,v= =v0,故A选项正确,当v<
=v0,故A选项正确,当v< =v0时,qvB<Eq,带电粒子向电场力一方偏移,电场力对带电粒子做正功,电势能减小,故B选项正确,C选项错误.带电粒子从下方进入时,电场力和洛伦兹力同向,电场力做正功,动能一定增加,故D选项正确.
=v0时,qvB<Eq,带电粒子向电场力一方偏移,电场力对带电粒子做正功,电势能减小,故B选项正确,C选项错误.带电粒子从下方进入时,电场力和洛伦兹力同向,电场力做正功,动能一定增加,故D选项正确.
本题难度:一般
5、计算题 (16分)如图所示,平行板电容器上板M带正电,两板间电压恒为U,极板长为(1+ )d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。
)d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。

(1)判断微粒的带电性质并求其电荷量与质量的比值;
(2)求匀强磁场的磁感应强度B的大小;
(3)若带电微粒从M板左侧边缘沿正对磁场圆心的方向射入板间电场,要使微粒不与两板相碰并从极板左侧射出,求微粒入射速度的大小范围。
参考答案:负电?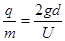 ?
?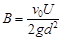 ?
?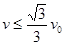

本题解析:(1)由题意可知,微粒所受电场力向上,上板带正电可得微粒带负电,(1分)
由于微粒做匀速直线运动可得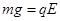 ?(1分)
?(1分)
又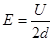 ?可得
?可得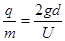 ?(2分)
?(2分)
(2) 由题意可得,微粒从下板P垂直射出,所以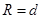 ?(1分)
?(1分)
根据牛顿第二定律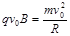 ?(2分)
?(2分)
解得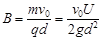 ?(2分)
?(2分)
(3)如图所示,要使粒子从左板射出,临界条件是恰从下板左边射出,此时根据几何关系可得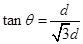 (2分)
(2分)
微粒做圆周运动的半径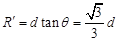 ?(1分)
?(1分)
又根据牛顿第二定律?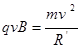 ?(1分)
?(1分)
解得?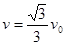 (2分)
(2分)
要使微粒从左板射出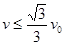 (1分)
(1分)
本题难度:一般