1、选择题  下列说法正确的是（　　）
A．合外力对质点做的功为零，则质点的动能、动量都一定不改变
B．合外力对质点施的冲量不为零，则质点的动量、动能都一定改变
C．某质点受到的合外力不为零，其动量、动能都一定改变
D．某质点的动量、动能都改变了，它所受到的合外力一定不为零

参考答案：
A、合外力对质点做的功为零，由动能定理知，动能一定不改变，但动量可能改变，比如匀速圆周运动．故A错误．
B、合外力对质点施加的冲量不为零，根据动量定理得知，质点的动量一定改变，但动能是标量，动能不一定改变．如果动量的大小没有改变，则动能不改变．故B错误．
C、某质点受到的合外力不为零，其动量一定改变，但动能不一定改变，比如匀速圆周运动．故C错误．
D、某质点的动量、动能都改变了，说明物体的速度大小和方向都改变了，一定有加速度，合外力一定不为零．故D正确．
故选D

本题解析：

本题难度：一般

2、选择题  质量为m的石子从距地面高为H的塔顶以初速v0竖直向下运动，若只考虑重力作用，则石子下落到距地面高为h处时的动能为(g表示重力加速度) (? )
A．mgH+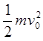
B．mgH-mgh
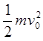C．mgH+-mgh
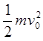D．mgH++mgh

参考答案：C

本题解析：由动能定理?mgH+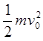-mgh，C对；

本题难度：一般

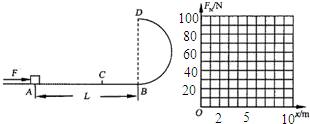
3、简答题  如图所示，固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接，轨道半径R=0.5m，一质量m=0.2kg的小物块（可视为质点）放在水平轨道上的A点，A与B相距L=10m，物块与水平轨道间的动摩擦因数μ=0.1．现用一水平恒力F向右推物块，已知F=3N，当物块运动到某点C时撤去该力，设C点到A点的距离为x．在圆轨道的最高点D处安装一压力传感器，当物块运动到D点时传感器就会显示相应的读数FN，压力传感器所能承受的最大压力为90N，g取10m/s2．
（1）当x=1m时，物块运动到圆轨道上的B点时对轨道的压力是多大？
（2）要使物块能够安全通过圆轨道的最高点D，求x的范围；
（3）在满足（2）问的情况下，在坐标系中作出压力传感器的读数FN与x的关系图象．

参考答案：（1）A到B的过程中推力与摩擦力做功，得：Fx-μmgL=12mvB2 ①
在B点时重力与支持力的合力提供向心力，得：NB-mg=mv2BR
联立解得：NB=6N根据牛顿第三定律可得NB′=NB=6N
（2）B到D的过程由动能定理得：
12mv2B=12mv2D+2mgR ②
到达D点时：FN+mg=mv2DR ③
联立①②③得：FN=2(Fx-μmgL)R-5mg=12x-18(N)
由于：0≤FN≤90N
解得：1.5≤x≤9m
（3）在坐标系中作出压力传感器的读数FN与x的关系图象如图．
答：（1）当x=1m时，物块运动到圆轨道上的B点时对轨道的压力是6N；
（2）要使物块能够安全通过圆轨道的最高点D，x的范围1.5≤x≤9N；
（3）在满足（2）问的情况下，在坐标系中作出压力传感器的读数FN与x的关系图象如图．

本题解析：

本题难度：一般

4、选择题  某人将一重物由静止举高h，并获得速度v，下列说法正确的是?（?）?
A．合外力物体做的功等于物体机械能的增加
B．物体克服重力做功等于物体动能的增加
C．人对物体做的功等于体克服重力做的功与物体获得动能之和
D．人对物体做的功等于物体机械能的增加

参考答案：CD

本题解析：合外力对物体做的功等于物体动能增加量，所以A错。克服重力做功等于重力势能增加两，所以B错。根据能量守恒定律人对物体做功，应等于物体重力势能增加量和动能增加量（机械能增加量），CD对。
点评：本题考查了动能定理以及机械能守恒定律的理解。在考虑问题时应优先使用动能定理，因为它不需要考虑条件。但是机械能守恒定律不需要求做功，因此在表达形式上要方便。

本题难度：简单

5、计算题  如图所示，图甲是杭州儿童乐园中的过山车的实物图片，图乙是过山车的原理图。在原理图中，半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道固定在倾角为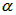=37°斜轨道面上的Q、Z两点，且两圆形轨道的最高点A、B均与P点平齐，圆形轨道与斜轨道之间圆滑连接。现使质量m=20kg的小车（视作质点）从P点以一定的初速度沿斜轨道向下运动。已知斜轨道面与小车间的动摩擦因数为μ=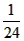，g=10m/s2，sin 37°=0.6，cos 37°=0.8。问：
（1）若小车能通过A、B两点，则小车在P点的初速度满足什么条件？
（2）若小车恰好能通过第二个圆形轨道的最高点B，则小车通过第一个圆形轨道最低点时，对轨道的压力大小是多少？
甲乙

参考答案：

解：（1）在B有：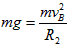
P点到B点的过程，由动能定理得：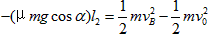
其中，l2为PZ之间的距离，根据几何关系可知满足：

解得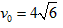：m∕s 即小车在P点初速度满足的条件为vp。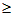
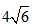（2）通过（1）问中的解可知，小车恰好能通过第二个圆形轨道的最高点B时，小车在P点初速度为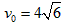m∕s 。
P点到A点的过程，由动能定理得：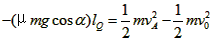
lQ为PQ之间的距离，根据几何关系可知满足：

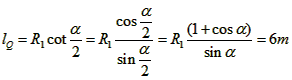
?设小车通过第一个圆形轨道最低点时的速度vc，由机械能守恒定律得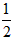：mvA2+2mgR1=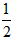m，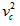
由牛顿定律得：FN-mg=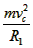
解得：FN=1920N
根据牛顿第三定律可得压力为1920N。

本题解析：

本题难度：困难