1、计算题  今年春季，我省极度干旱，缺水严重，部分地区用高射炮进行人工降雨来缓解旱情，已知所用高射炮的质量为M =5t，炮弹离开炮口时的速度为v=600m/s，炮弹的质量为m =10kg，发射时炮口和地面成60°角，求炮弹离开炮口时炮车后退速度？

参考答案：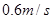

本题解析： 炮弹离开炮口时，炮弹和炮车在水平方向没有受到外力，则在水平方向动量守恒，取炮车后退的方向为正，则有：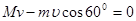
解得：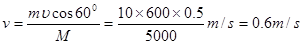
点评：关键是判断炮弹在水平方向上动量守恒，

本题难度：简单

2、选择题  如图所示，与轻弹簧相连的物体A停放在光滑的水平面上。物体B沿水平方向向右运动，跟与A相连的轻弹簧相碰。在B跟弹簧相碰后，对于A、B和轻弹簧组成的系统，下列说法中不正确的是（?）

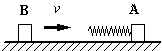
A．弹簧压缩量最大时，A、B的速度相同
B．弹簧压缩量最大时，A、B的动能之和最小
C．弹簧被压缩的过程中系统的总动量不断减小
D．物体A的速度最大时，弹簧的弹性势能为零

参考答案：C

本题解析：B的速度先比A大 后比A小 A、B的速度相同时 弹簧的压缩量最大 然后B会继续减速 A加速，A正确；整个系统外力之和为零 总能量不变 弹簧压缩量最大时?弹性势能最大 动能最小 就是A、B的动能之和最小，B正确；整个系统外力之和为零 所以系统动量守恒 总动量不变，C错误；物体A的速度最大时 弹簧没有内压缩 否则A会继续加速，D正确；故选C
点评：关键是根据两物体的速度变化，判断弹簧的压缩程度

本题难度：一般

3、简答题  在“验证动量守恒定律”的实验中，使用半径相同均为1 cm的两个小球A和B，它们的质量之比mA∶mB=3∶8，实验结果如图所示，O点为斜槽末端所装重垂线的竖直投影点，M、P、N为小球在白纸上的落点位置，且O、M、P、N在同一直线上.试用图示刻度尺上读出的数据和题设条件验证两小球碰撞前后的动量是否守恒.

参考答案：动量守恒

本题解析：由mA∶mB=3∶8得mA=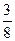mB
B球碰前的速度vB可用OP表示，OP="16.4" cm；B球碰后的速度可用OM表示，OM="8.0" cm，A球碰后的速度可用（ON-2r)表示，ON-2r="23.3" cm.
碰前的总动量
p=mBOP=16.4mB
碰后的总动量
p′=mBOM+mA(ON-2r)=8.0mB+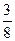mB×23.3=16.7mb
在误差许可的范围内，p′=p,即两球碰前的总动量等于两球碰后的总动量，验证了动量守恒定律.

本题难度：简单

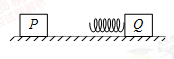
4、计算题  如图所示，位于光滑水平桌面上的小滑块P和Q均可视为质点，质量均为m，Q与轻质弹簧相连并处于静止状态，P以初速度v向Q运动 并与弹簧发生作用．求整个过程中弹簧的最大弹性势能．

参考答案：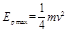

本题解析：由动量守恒得 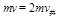    （1分）
由能量守恒定律得 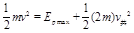（2分）
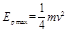 （1分）
考点：本题考查动量守恒

本题难度：一般

5、计算题  如图甲所示，一个小弹丸水平射入一个原来静止的单摆并留在里面，结果单摆的振动图线如图乙所示.已知摆球质量为小弹丸质量的5倍，试求小弹丸射入摆球的速度是多大？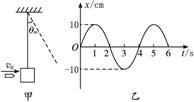

参考答案：0.94 m/s

本题解析：弹丸水平击中摆球的过程动量守恒，从图中可以读出振幅A和周期T，可求振动的最大速度，进而可求弹丸的速度.
设小弹丸的速度为v0，击入摆球后，摆球的速度为vm
最大偏角为θm，摆球质量为m.
根据机械能守恒定律有：
Ekm=Epm
即mvm2=mgl(1-cosθm)
=2mgl·sin2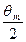
≈2mgl(·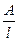)2
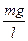=×A2
解之得：vm=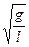A
又由单摆周期公式有：
T=2π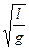
由以上各式得：vm=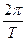A
从图乙中可以读出A="0.1" m，T="4" s.
则摆球振动的最大速度为
vm== 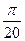m/s
根据动量守恒定律，有
mv0=(m+5m)vm
所以v0=6×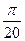 m/s="0.94" m/s

本题难度：一般