1、简答题  如图，ABCD是边长为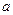的正方形。质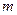量为、电荷量为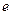的电子以大小为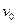的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场。电子从BC边上的任意点入射，都只能从A点射出磁场。不计重力，求：

（1）次匀强磁场区域中磁感应强度的方向和大小；
（2）此匀强磁场区域的最小面积。

参考答案：见解析

本题解析：（1）设匀强磁场的磁感应强度的大小为B。令圆弧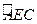是自C点垂直于BC入射的电子在磁场中的运行轨道。电子所受到的磁场的作用力


应指向圆弧的圆心，因而磁场的方向应垂直于纸面向外。圆弧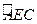的圆心在CB边或其延长线上。依题意，圆心在A、C连线的中垂线上，故B 点即为圆心，圆半径为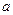按照牛顿定律有

联立①②式得

（2）由（1）中决定的磁感应强度的方向和大小，可知自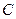点垂直于入射电子在A点沿DA方向射出，且自BC边上其它点垂直于入射的电子的运动轨道只能在BAEC区域中。因而，圆弧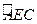是所求的最小磁场区域的一个边界。
为了决定该磁场区域的另一边界，我们来考察射中A点的电子的速度方向与BA的延长线交角为（不妨设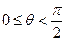）的情形。该电子的运动轨迹如右图所示。
图中，圆的圆心为O，pq垂直于BC边，由③式知，圆弧的半径仍为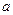，在D为原点、DC为x轴，AD为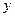轴的坐标系中，P点的坐标为

这意味着，在范围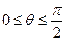内，p点形成以D为圆心、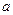为半径的四分之一圆周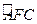，它是电子做直线运动和圆周运动的分界线，构成所求磁场区域的另一边界。
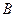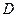因此，所求的最小匀强磁场区域时分别以和为圆心、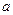为半径的两个四分之一圆周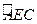和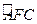所围成的，其面积为

本题难度：一般

2、简答题  如图所示，以O为原点建立平面直角坐标系Oxy，沿y轴放置一平面荧光屏，在y＞0，0＜x＜0.5m的区域有垂直于纸面向里的匀强磁场，磁场的磁感应强度大小B=0.5T．在原点O放一个开有小孔粒子源，粒子源能同时放出比荷为q/m=4.0×106kg/C的不同速率的正离子束，沿与x轴成30°角从小孔射入磁场，最后打在荧光屏上，使荧光屏发亮．入射正离子束的速率在0到最大值vm=2.0×106m/s的范围内，不计离子之间的相互作用，也不计离子的重力．
（1）求离子打到荧光屏上的范围．
（2）若在某时刻（设为t=0时刻）沿与x轴成30°角方向射入各种速率的正离子，求经过

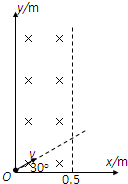
参考答案：（1）由qvB=mv2r得，r=mvqB，rm=mvmqB=1m




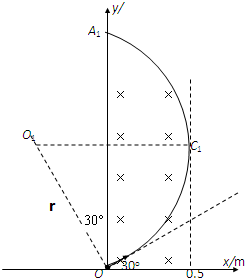
离子在磁场中运动最大轨道半径：rm=1m
由几何关系知，最大速度的离子刚好沿磁场边缘打在荧光屏上，如左图所示．
所以OA1长度为：y=2rcos300=

本题解析：

本题难度：一般

3、简答题  如图所示，一个质量为m，电荷量为e的质子从O点以速度v0垂直NP板射入两板之间区域，两个板间存在垂直纸面向里的匀强磁场，已知两板之间距离为d，板长也为d，O点是NP板的正中间，为使粒子能射出两板间，试求磁感应强度B的大小．

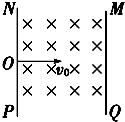
参考答案：当粒子从a点射出时，轨迹半径最小，设为r1．对应的速度最小，设为v1．当粒子从从b点射出时，轨迹半径最大，设为r2．对应的速度最大，设为v2．根据几何关系得：
r1=14d，
r22=d2+（r2-12d）2
则得：r2=54d，
根据牛顿第二定律得：ev0B=mv02r
得：B=mv0qr
故有：B1=4mv0de，B2=5mv04de
所以要使粒子能从ab边射出磁场，v0的大小范围为5mv04de≤B≤4mv0de．
答：要使粒子能从ab边射出磁场，v0的大小范围为5mv04de≤B≤4mv0de．

本题解析：

本题难度：一般

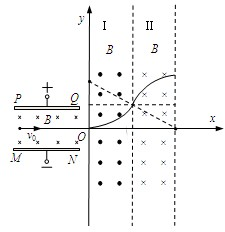
4、简答题  如图所示，带电平行金属板PQ和MN之间的距离为d，金属板之间有垂直纸面向外的匀强磁场，磁感应强度大小为B，x轴与金属板中心线重合，y轴垂直于金属板，在区域Ⅰ和区域Ⅱ内存在方向相同的匀强磁场，磁感应强度大小分别为B1和B2，且B1＜B2，一电子沿着x轴正向以速度v0射入平行板之间，在平行板间恰好沿着x轴正方向做直线运动，并由区域Ⅰ进入区域Ⅱ，然后经过y轴离开区域Ⅰ，已知区域Ⅰ沿x轴方向宽度为

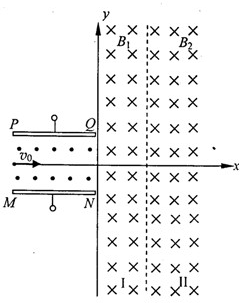
参考答案：（1）粒子在板间做直线运动，则洛伦兹力和电场力相等：ev0B=eUd
得：U=Bv0d
（2）粒子的轨迹如图，在区域I、II内，由qvB=mvR得：
R1=mv0eB1
同理：R2=mv0eB2
（3）由几何关系可知：LR1=sinθ1
得：θ1=60°
θ1=θ2=60°
由：T=2πRv
得：T=2πmqB
则t1=16T1=πm3eB1
t2=16T2=πm3eB2
t=2t1+t2=πm3e(2B1+1B2)
答：（1）两金属板之间电势差U为Bv0d；
（2）电子在区域Ⅰ和区域Ⅱ中运动的半径R1和R2分别为mv0eB1、mv0eB2；
（3）电子两次经过y轴的时间间隔t为πm3e（2B1+1B2）．

本题解析：

本题难度：一般

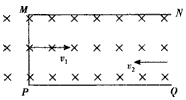
5、选择题  如图所示，用一块金属板折成横截面为“”形的金属槽放在磁感应强度为B的匀强磁场中，并以速度v1向右匀速运动，从槽口右侧射入的带电微粒的速度是v2，如果微粒进入槽后恰能做匀速度周运动，则微粒做匀速圆周运动的轨道半径r和周期T分别为（ ? ）

参考答案：B

本题解析：

本题难度：一般