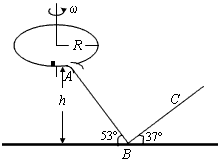
1、计算题  如图所示，一水平圆盘绕过圆心的竖直轴转动，圆盘边缘有一质量m＝1.0 kg的小滑块。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，经光滑的过渡圆管进入轨道ABC。已知AB段斜面倾角为53°，BC段斜面倾角为37°，滑块与圆盘及斜面间的动摩擦因数均μ＝0.5，A点离B点所在水平面的高度h＝1.2 m。滑块在运动过程中始终未脱离轨道，不计在过渡圆管处和B点的机械能损失，最大静摩擦力近似等于滑动摩擦力，取g＝10 m/s2，sin37°＝0.6，cos37°＝0.8。
（1）若圆盘半径R＝0.2 m，当圆盘的角速度多大时，滑块从圆盘上滑落？
（2）若取圆盘所在平面为零势能面，求滑块到达B点时的机械能。
（3）从滑块到达B点时起，经0.6 s正好通过C点，求BC之间的距离。

参考答案：解：（1）滑块在圆盘上做圆周运动时，静摩擦力充当向心力，根据牛顿第二定律，可得：μmg＝mω2R
代入数据解得：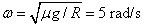
（2）滑块在A点时的速度：vA＝ωR＝1 m/s
从A到B的运动过程由动能定理得：mgh－μmgcos53°×h/sin53°＝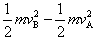
在B点时的机械能为：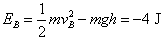
（3）滑块在B点时的速度：vB＝4 m/s
滑块沿BC段向上运动时的加速度大小：a1＝g(sin37°＋μcos37°)＝10 m/s2
返回时的加速度大小：a2＝g(sin37°－μcos37°)＝2 m/s2
BC间的距离：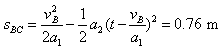

本题解析：

本题难度：一般

2、选择题  带电粒子M只在电场力作用下由P点运动到Q点，在此过程中克服电场力做了2.6×10-6J?的功．那么，（　　）
A．M在P点的电势能一定小于它在Q点的电势能
B．P点的场强一定小于Q点的场强
C．P点的电势一定高于Q点的电势
D．M在P点的动能一定大于它在Q点的动能

参考答案：A、从题目可知克服电场力做功，即电场力做负功，故电势能增加，P点的电势能一定小于它在Q点的电势能，故A正确；
B、电场分布情况不知，无法判断P点和Q点电场强度的大小关系，故B错误；
C、因为电荷正负不知，故无法判断电势高低，C错误；
D、因为只有电场力做功，因此只有电势能和动能之间的转化，电势能增加，则动能减小，故D正确．
故选AD．

本题解析：

本题难度：简单

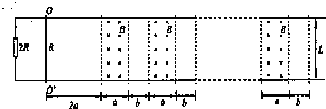
3、简答题  如图所示，两根相距为L的金属轨道固定于水平面上，导轨电阻不计；一根质量为m、长为L、电阻为R的金属棒两端放于导轨上，导轨与金属棒间的动摩擦因数为μ，棒与导轨的接触电阻不计．导轨左端连有阻值为2R的电阻．轨道平面上有n段竖直向下的宽度为a、间距为b的匀强磁场（a＞b），磁感应强度为B．金属棒初始位于OO′处，与第一段磁场相距2a．求：
（1）若金属棒有向右的初速度v0，为使金属棒保持v0的速度一直向右穿过各磁场，需对金属棒施加水平向右的拉力．求金属棒不在磁场中时受到的拉力F1，和在磁场中时受到的拉力F2的大小；
（2）在（1）的情况下，求金属棒从OO′开始运动到刚离开第n段磁场过程中，拉力所做的功；
（3）若金属棒初速度为零，现对其施以水平向右的恒定拉力F，使棒进入各磁场的速度都相同，求金属棒从OO′开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量．

参考答案：
（1）当金属棒匀速运动时，
? 进入磁场前，F1=μmg?
?进入磁场后，F2=μmg+F安?
?又F安=BIL
?I=BLV03R?
?解得：F2=μmg+B2L2v03R
?（2）金属棒在磁场外运动过程中，
? W1=μmg[2a+（n-1）b]
? ? 穿过 n?段磁场过程中，W2=nF2a
? 故拉力做功为：W=W1+W2=μmg[2a+（n-1）b]+nF2a=μmg[(n+2)a+(n-1)b]+n?B2L2v0a3R?
?（3）金属棒进入第一段磁场前，(F-μmg)?2a=12m?v21
? 穿过第一段磁场过程中，Fa-μmga-E电1=12mv22-12mv21
? 金属棒从穿出第一段磁场到进入第二段磁场的过程中，(F-μmg)b=12mv21-12mv22?
? 得到，E电1=（F-μmg）（a+b）
? 从OO′开始运动到刚离开第n段磁场整个过程中电路中产生总热量E电=n（F-μmg）（a+b）
? 由于金属棒与电阻的感应电流瞬时相等，根据焦耳定律Q=I2Rt，Q∝R
? 整个过程中电阻上产生的总热量为：Q=n2R3RE电
? 解得：Q=23n(F-μmg)(a+b)
答：（1）金属棒不在磁场中时受到的拉力F1=mg，在磁场中时受到的拉力F2的大小为μmg+B2L2v03R；
? （2）拉力所做的功为μmg[(n+2)a+(n-1)b]+n?B2L2v0a3R；?
? （3）金属棒从OO′开始运动到刚离开第n段磁场整个过程中导轨左端电阻上产生的热量为23n(F-μmg)(a+b)．

本题解析：

本题难度：一般

4、简答题  质量为 m =" 50" kg的滑雪运动员，以初速度 v0 =" 4" m/s ，从高度为 h =" 10" m的弯曲滑道顶端 A 滑下，到达滑道底端 B 时的速度 vt =" 10" m/s ．求：滑雪运动员在这段滑行过程中克服阻力做的功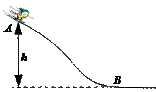

参考答案：
2900J

本题解析：
设摩擦力做功为Wf ?，
根据动能定理：mgh－wf=1/2mvt2－1/2mv02-----------5分
带入数值得：Wf =2900J-----------------------------3分

本题难度：简单

5、计算题  如图所示，倾角θ=30°，宽度L=1m的足够长的U形平行光滑金属导轨，固定在磁感应强度B=1T，范围充分大的匀强磁场中，磁场方向与导轨平面垂直．用平行于导轨、功率恒为6W的牵引力F牵引一根质量m=0．2kg，电阻R=1Ω。放在导轨上的金属棒ab，由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直)，当ab棒移动2．8m时获得稳定速度，在此过程中，金属棒产生的热量为5．8J(不计导轨电阻及一切摩擦，取g=10m／s2)，

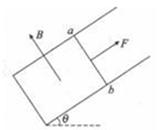
求：(1)ab棒的稳定速度；(2)ab棒从静止开始达到稳定速度所需时间．

参考答案：(1) v1=2m／s(2) t=1．5s

本题解析：(1)ab棒达到稳定速度后，应具有受力平衡的特点，设此时棒ab所受安培力为FB．则F－mgsin30°+FB，而FB=BIL=B2L2v/R，牵引力F=P/v，得P/v ="mgsin30°+" B2L2v/R
代人数据后得v1=2m／s，v2=-3m／s(舍去)
(2)设从静止到稳定速度所需时间为t．棒ab从静止开始到具有稳定速度的过程中在做变加速直线运动，据动能定理有：Pt-mgsin30°·s—Q=mv2/2－0，代人数据得t=1．5s。
点评：难度中等，能够根据导体棒匀速运动判断受力平衡，并列出受力平衡的关系式是求解本题的关键

本题难度：一般