1、计算题  如图14所示，一块磁铁放在铁板ABC上的A处，其中AB长为lm，BC长为0.8m，BC与水平面间的夹角为37°，磁铁与铁板间的引力为磁铁重的0.2倍，磁铁与铁板间的动摩擦因数μ=0.25，现在给磁铁一个水平向左的初速度v0=4m/s。不计磁铁经过B处的机械能损失，取g=10m/s2，已知sin37°=0.6，cos37°=0.8。则：

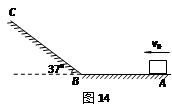
（1）求磁铁第一次到达B处的速度大小；
（2）求磁铁在BC上向上运动的加速度大小；
（3）请分析判断磁铁最终能否第二次到达B点。

参考答案：（1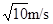）；（2）a = 8.5m/s2；（3）能第二次到达B点。

本题解析：分析：（1）小磁铁从A点到第一次到达B点的过程中，摩擦力做负功，摩擦力大小为f=μ（mg+F），F为磁铁与铁板的引力，F=0.2mg，根据动能定理求解小磁铁第一次到达B处的速度大小；
（2）小磁铁在BC段向上运动时受到重力、支持力和沿斜面向下的滑动摩擦力．滑动摩擦力大小为f=μ（mgcos37°+F），根据牛顿第二定律求解加速度．
（3）根据速度位移公式求出磁铁沿斜面向上运动至速度为零时经过的位移，与斜面的长度比较，再分析小磁铁能否第二次到达B处．
解答：解：（1）对磁铁在AB段进行受力分析如图所示，磁铁与铁板的引力为F=0.2mg，
根据动能定理得
-fx1=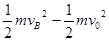
代入数据解得vB=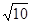m/s
（2）对磁铁在BC段受力分析，有摩擦力f′=μ（mgcos37°+F）．根据牛顿第二定律得
mgsin37°+f′=ma
代入解得a2=8.5m/s2．?
（3）磁铁以初速vB沿斜面向上运动至速度为零时其经过的位移为
x=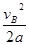=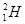m<0.8m
故磁铁不会滑出BC面，会第二次到达B处．?
答：
（1）小磁铁第一次到达B处的速度大小是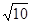m/s；
（2）小磁铁在BC段向上运动时的加速度大小8.5m/s2；
（3）小磁铁能第二次到达B处．
点评：本题比通常的问题只多个磁铁的引力，其他的解题方法和步骤都相同，中等难度．

本题难度：一般

2、简答题  如图所示，一质量为m带正电的小球，用长为L的绝缘细线悬挂于O点，处于一水平方向的匀强电场中，静止时细线右偏与竖直方向成45°角，位于图中的P点．重力加速度为g，求：
（1）静止在P点时线的拉力是多大？
（2）如将小球向右拉紧至与O点等高的A点由静止释放，则当小球摆至P点时，其电势能如何变？变化了多少？
（3）如将小球向左拉紧至与O点等高的B点由静止释放，则小球到达P点时的速度大小？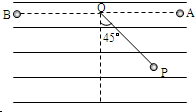

参考答案：（1）小球静止在P点时由平衡条件得
? cos45°=mgT
?T=

本题解析：

本题难度：一般

3、选择题  如图4所示，A、B两物体用一根跨过定滑轮的细绳相连，置于固定斜面体的两个斜面上的相同高度，处于静止状态，两斜面的倾角分别为37°和53°，若不计摩擦，剪断细绳后，下列说法中正确的是(以地面为参考面)(? )

A．两物体着地时的速度相同。?
B．两物体着地时的动能一定相同。
C．两物体着地时的机械能一定不同。?
D．两物体着地时所受重力的功率一定相同。

参考答案：CD

本题解析：两物体开始处于同样高度，运动到最低点时由动能定理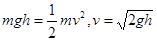，速度大小相等，但方向不同，A错；由于两物体质量不同，到达最低点时动能不同，C对；处于静止状态时，，到最低点时A的重力功率为，B的重力功率为，功率相等，D对；

本题难度：简单

4、简答题  如图所示，相距为d的A、B两平行金属板足够大，板间电压恒为U，有一波长为λ的细激光束照射到B板中央，使B板发生光电效应．已知普朗克恒量为h，金属板B的逸出功为W，电子质量为m，电荷量e，求：
（1）从B板运动到A板所需时间最短的光电子，到达A板时的动能；
（2）光电子从B板运动到A板时所需的最长时间．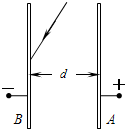

参考答案：（1）根据爱因斯坦光电效应方程?EK=hv-W?…①
光子的频率：ν=Cλ…②
所以，光电子的最大初动能：EK=hCλ-W…③
能以最短时间到达A板的光电子，是初动能最大且垂直于板面离开B板的电子，设到达A板时的动能为EK1，
由动能定理：eU=EK1-EK…④
所以：EK1=eU+hCλ-W…⑤
（2）能以最长时间到达A板的光电子，是离开B板时的初速度为零或运动方向平行于B板的光的电子．
∵d=12at2=12Uemdt2…⑥
∴t=d

本题解析：

本题难度：一般

5、简答题  跳水运动是我国体育运动的优势项目，某运动员参加10m跳台的跳水比赛，如其质量为m=60kg，其体形可等效为长度L=1.0m，直径d=0.3m的圆柱体，不计空气阻力，运动员站立在跳台上向上跳起到达最高点时，他的重心离跳台台面的高度为1.3m，在从起跳到接触水面过程中完成一系列动作，入水后水的等效阻力F（未包含浮力）作用于圆柱体的下端面，F的数值随入水深度y变化的函数图象如图所示，该直线与F轴相交于F=2.5mg处，与y轴相交于y=h?（某一未知深度），已知水的密度ρ=1×103㎏/m3，根据以上的数据进行估算（g取10m/s2）．
（1）运动员起跳瞬间所做的功；
（2）运动员起跳瞬间获得的速度大小；
（3）运动员刚接触到水面瞬间的动能；
（4）运动员入水可以达到的最大深度h?（结果保留两位有效数字）．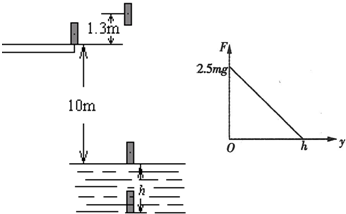

参考答案：（1）运用动能定理研究运动员站立在跳台上向上跳起到达最高点得：
运动员起跳瞬间所做的功为W，
W-mgh1=0-0
W=60×10×（1.3-0.5）=480J
（2）运动员起跳过程
W=12mv2-0?
v=4m/s
（3）运动员从起跳到刚接触水面，运用动能定理得：
mgh′=Ek′-12mv2
解得：运动员刚接触到水面瞬间的动能Ek′=6480J．
（4）运动员从刚接触水面到最深处
mgh-12×2.5mgh-12ρgVL-ρgV（h-L）=0-12mvˊ2
体积V=π（d2）2?L
解得：h=7.98m
答：（1）运动员起跳瞬间所做的功是480J；
（2）运动员起跳瞬间获得的速度大小是4m/s；
（3）运动员刚接触到水面瞬间的动能是6480J；
（4）运动员入水可以达到的最大深度是7.98 m

本题解析：

本题难度：一般