微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
1、选择题 如图宽度为d的有界匀强磁场,磁感应强度为B,方向垂直纸面向里,MM′和NN′是它的两条边界.现有质量为m,电量为+q的带电粒子沿图示方向与磁场边界夹角为60°垂直磁场射入.要使粒子不能从边界NN′射出,则粒子入射速率的最大值是( )
A.
B.
C.
D.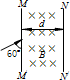
参考答案:
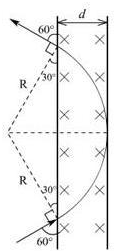
设带电粒子速率为v,轨迹半径为R,则由牛顿第二定律得,
? qvB=mv2R
得到,R=mvqB,可见,带电粒子速率越大,轨迹半径越大,当轨迹恰好与边界NN′相切时,粒子恰好不能从边界NN′射出,如图,由几何知识得到,R=2d.
则粒子入射速率的最大值v=qBRm=2qBdm.
故选A
本题解析:
本题难度:一般
2、选择题 如图所示,在平面直角坐标系中有一个垂直于纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L)。?一质量为m、电荷量为e的电子从a点以初速度v0沿x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度方向与x轴正方向的夹角为60°。下列说法正确的是:
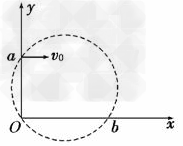
[? ]
A、电子在磁场中运动的时间为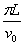
B、电子在磁场中运动的时间为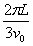
C、磁场区域的圆心坐标为 (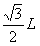 ,
,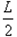 )
)
D、电子在磁场中做圆周运动的圆心坐标为(0,-2L)
参考答案:BC
本题解析:
本题难度:一般
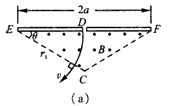
3、计算题 如图所示,在一底边长为2a,θ=30°的等腰三角形区域内(D为底边中点),有垂直于纸面向外的匀强磁场。现有一质量为m,电荷量为q的带正电的粒子从静止开始经过电势差为U的电场加速后,从D点垂直于EF进入磁场,不计重力与空气阻力的影响。
(1)若粒子恰好垂直于EC边射出磁场,求磁场的磁感应强度B为多少?
(2)改变磁感应强度的大小,粒子进入磁场偏转后能打到ED板,求粒子从进入磁场到第一次打到ED板的最长时间是多少?
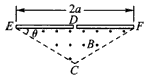
参考答案:解:(1)依题意,设粒子经电场加速射入磁场时的速度为v
由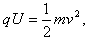 得
得 ?①
?①
粒子在磁场中做匀速圆周运动,其圆心在E点,如图(a)所示,半径r1=a ②
由洛伦兹力提供向心力 ?③
?③
由①②③式得
(2)粒子速率恒定,从进入磁场到第一次打到ED板的轨迹与EC边相切时,路程最长,运动时间最长,如图(b)所示,设轨迹半径为r2
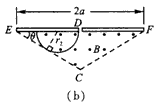
由图中几何关系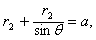 得
得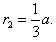
最长时间
由以上各式联立得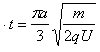
本题解析:
本题难度:困难
4、选择题 如图,在x>0、y>0的空间中有恒定的匀强磁场,磁感应强度的方向垂直于xOy平面向里,大小为B.现有一质量为m、电荷量为q的带正电粒子,在x轴上到原点的距离为x0的P点,以平行于y轴的初速度射入此磁场,在磁场作用下沿垂直于y轴的方向射出此磁场.不计重力的影响.由这些条件可知?
A.不能确定粒子通过y轴时的位置
B.不能确定粒子速度的大小
C.不能确定粒子在磁场中运动所经历的时间
D.以上三个判断都不对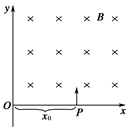
参考答案:D
本题解析:由题意可知,带电粒子要垂直于y轴离开磁场,可得知带电粒子逆时针运动,由左手定则可判断粒子带正电;带电粒子在磁场中的运动轨迹如图所示,可知离开磁场通过y轴时的位置的位置为y=x0;并得到运动的半径为R=x0,由半径公式R=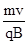
可求出粒子的速度为v=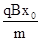 ;带电粒子是垂直于y轴离开磁场的,顾可知带电粒子在磁场中运动了
;带电粒子是垂直于y轴离开磁场的,顾可知带电粒子在磁场中运动了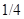 圆周,即时间是
圆周,即时间是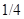 T,又因T=
T,又因T=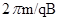 ,粒子的运动时间为
,粒子的运动时间为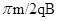 .故选D
.故选D
本题难度:一般
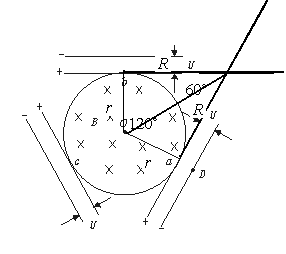
5、计算题 (12分)如图所示,有一半径为r的圆形有界匀强磁场区域,磁感应强度为B,方向垂直纸面向里,其周围对称放置带有中心孔a、b、c的三个相同的平行板电容器,三个电容器两板间距离均为d,接有相同的电压U,在D处有一静止的电子,质量为m,电荷量为e,释放后从a孔射入匀强磁场中,并先后穿过b、c孔再从a孔穿出回到D处,求:?
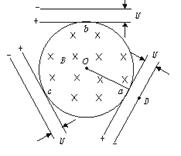
(1)电子在匀强磁场中运动的轨道半径R;
(2)匀强磁场的磁感应强度B;?
(3)电子从D出发到第一次回到D处所用的时间t。
参考答案:(1)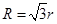 (2)
(2)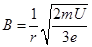 (3)
(3)
本题解析:(1)带电粒子在匀强磁场中做匀速圆周运动,从 a点进从b点出,粒子运动的半径和磁场半径的几何关系如下图,可得
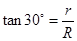
解得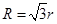
(2)粒子在平行板电容器中从D到A,经加速电场加速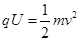
粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力即
带入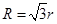 解得磁感应强度
解得磁感应强度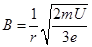
(3)根据运动电荷在磁场中做匀速圆周运动的周期公式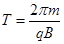 ,依题意分析可知电子在磁场中运动一次所经历的时间为
,依题意分析可知电子在磁场中运动一次所经历的时间为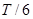 ,故电子在磁场中运动的总时间
,故电子在磁场中运动的总时间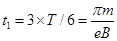 ;
;
而电子在匀强电场中做一类 似竖直上抛运动,所经历的时间 ,由
,由 可求得:
可求得: 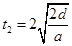 .
.
因为 , 所以
, 所以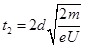 ,.?
,.?
故电子从出发至第一次回到出发点D处所用的时间为:?
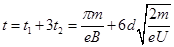 .?
.?
 ?(4分)
?(4分)
本题难度:一般