1、简答题  [选修3-5]
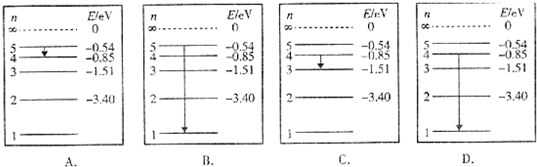
（1）已知处于某一能级n上的一群氢原子向低能级跃迁时，能够发出10种不同频率的光，下列能表示辐射光波长最长的那种跃迁的示意图是

（2）在实验室内较精准地测量到的双β衰变事例是在1987年公布的，在进行了7960小时的实验后，以68%的置信度认出

参考答案：（1）由图示可知，在A所示能级跃迁中释放光子的能量最小，辐射光波的波长越长．
（2）8234Se中有82-34=48个中子，发生双β衰变时有两个中子释放出电子而变为质子，则衰变后中子数为46个；
由质能方程可得，衰变过程中质量亏损△m=Ec2．
（3）以两球组成的系统为研究对象，系统动量守恒，
以A球的初速度方向为正方向，由动量守恒定律得：
mv0=m（-13v0）+2mvB，解得：vB=23v0，
碰后系统的总动能E=12m（-13mv0）2+12×2m（23v0）2=12mv02，
则碰撞前后系统机械能没有损失，则碰撞为弹性碰撞．
故答案为：（1）A；（2）46；Ec2；（3）碰撞为弹性碰撞．

本题解析：

本题难度：简单

2、简答题  静止的质量为M的原子核发生一次α衰变．已知衰变后的α粒子的质量为m、电荷量为q、速度为v，并假设衰变过程中释放的核能全部转化为α粒子和新核的动能．（注：涉及动量问题时，亏损的质量可忽略不计）
求：（1）衰变后新核反冲的速度大小；
（2）衰变过程中的质量亏损．

参考答案：（1）由动量守恒定律得：mv-（M-m）v"=0，
解得，新核的速度：v′=mM-mv；
（2）原子核衰变释放的能量：△E=12mv2+12(M-m)v′2，
由质能方程得：△E=△m?c2，
解得：△m=mMv22(M-m)c2；
答：（1）衰变后新核反冲的速度大小为mvM-m；
（2）衰变过程中的质量亏损为mMv22(M-m)c2．

本题解析：

本题难度：一般

3、简答题  如图，水平足够长光滑固定直杆AB上穿有质量为M的滑块，其上用光滑铰链着一个长为L的轻杆，杆的另一端固定着一个质量为M的小球，初始时，系统静止，轻杆水平。
小题1:1给小球以竖直向上的初速v01，球到达最高点时杆与水平方向呈θ角，（θ<900），求v01。
小题2:2给小球以竖直向上的初速v02，球到达最高点时的速度为v，求v02。
?

参考答案：
小题1:?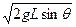
小题2: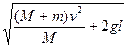

本题解析：
小题1:此题中须弄清的几个问题是，小球上升过程中，滑块是向左还是向右运动；小球到达最高点时是否有速度；此时滑块的速度方向如何；我们不妨这样来分析，若没有杆连接，则滑块不动，且小球将竖直向上运动。即最初杆有被拉伸的趋势。则滑块将向左运动。运动中小球和滑块在水平方向上不受外力，所以系统水平方向上动量守恒，①问中，假设小球在最高点时有水平向左的速度，则由水平方向动量守恒得滑块将有向右的速度，则上面的分析可知，滑块向左运动中出现向右的速度这是不可能的；若小球在最高点时有向左的速度，则由水平方向动量守恒可知，这时滑块将具有水平向左的速度，二者速度相反，则小球还是要上升，那么此时的位置就不是最高的；若小球具有向上或向下的速度，即小球处于上升或下降的过程中，则小球此时的位置也不是最高的。
①问中小球在最高点时不可能有速度。即速度为0，则由系统水平方向动量守恒得滑块此时的速度也是0，
则由系统机械能守恒（并非小球的机械能守恒）
得?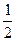mv012＝mgLsinθ，?解得v01＝?
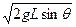小题2:2问中小球在最高点时的速度不为0，即小球到达最高点时轻杆竖直且速度向右。
由水平方向动量守恒得
mv－Mvx＝0
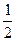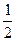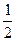又由系统机械能守恒mv022＝mgL+mv2+Mvx2
以上两式联立，可解得v02＝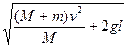

本题难度：简单

4、计算题  如图所示，质量为3m、长度为L的木块置于光滑的水平面上，质量为m的子弹以初速度v0水平向右射入木块，穿出木块时速度为2v0/5，设木块对子弹的阻力始终保持不变。
（1）求子弹穿透木块后，木块速度的大小；
（2）求子弹穿透木块的过程中，木块滑行的距离s；
（3）若改将木块固定在水平传送带上，使木块始终以某一恒定速度（小于v0）水平向右运动，子弹仍以初速度v0水平向右射入木块。如果子弹恰能穿透木块，求此过程所经历的时间。

参考答案：解：（1），则。?
（2）
解之得。
（3）
解之得。

本题解析：

本题难度：一般

5、计算题  某同学利用如图所示的装置验证动量守恒定律。图中两摆摆长相同，悬挂于同一高度，A、B两摆球均很小，质量之比为1：2。当两摆均处于自由静止状态时，其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角，然后将其由静止释放。结果观察到两摆球粘在一起摆动，且最大摆角成30°。若本实验允许的最大误差为±4％，此实验是否成功地验证了动量守恒定律？

参考答案：此实验在规定的范围内验证了动量守恒定律

本题解析：设摆球A、B的质量分别为mA、mB，摆长为l，B球的初始高度为h1，碰撞前B球的速度为vB.在不考虑摆线质量的情况下，根据题意及机械能守恒定律得①
②
设碰撞前后两摆球的总动量大小分别为P1、P2，则③
联立①②③式可得④
同理可得⑤
联立④⑤可得⑥
代入已知条件得⑦
⑧
所以，此实验在规定的范围内验证了动量守恒定律。

本题难度：一般