1、计算题  一个质量为M的雪橇静止在水平雪地上，一条质量为m的爱斯基摩狗站在该雪橇上。狗向雪橇的正后方跳下，随后又追赶并向前跳上雪橇；其后狗又反复地跳下、追赶并跳上雪橇，狗与雪橇始终沿一条直线运动。若狗跳离雪橇时雪橇的速度为V，则此时狗相对于地面的速度为V+u(其中u为狗相对于雪橇的速度，V+u为代数和。若以雪橇运动的方向为正方向，则V为正值，u为负值)。设狗总以速度v追赶和跳上雪橇，雪橇与雪地间的摩擦忽略不计。已知v的大小为5m/s，u的大小为4m/s，M=30kg，m=10kg。
（1）求狗第一次跳上雪橇后两者的共同速度的大小。
（2）求雪橇最终速度的大小和狗最多能跳上雪橇的次数。（供使用但不一定用到的对数值：lg2=0.301，lg3=0.477)

参考答案：解：（1）设雪橇运动的方向为正方向，狗第1次跳下雪橇后雪橇的速度为V1，根据动量守恒定律，有

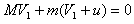
狗第1次跳上雪橇时，雪橇与狗的共同速度V1"满足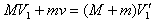
可解得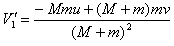
将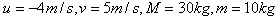代入，得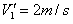
（2）设雪橇运动的方向为正方向，狗第（n－1）次跳下雪橇后雪橇的速度为Vn－1，则狗第（n－1）次跳上雪橇后的速度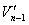满足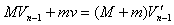
这样，狗n次跳下雪橇后，雪橇的速度为Vn满足
解得
狗追不上雪橇的条件是Vn≥v
可化为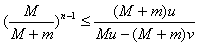
最后可求得
代入数据，得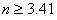
狗最多能跳上雪橇3次，雪橇最终的速度大小为V4=5.625m/s

本题解析：

本题难度：困难

2、计算题  在纳米技术中需要移动或修补原子，必须使在不停地做热运动（速率约几百米每秒）的原子几乎静止下来且能在一个小的空间区域内停留一段时间，为此已发明了“激光致冷”的技术．若把原子和入射光子分别类比为一辆小车和一个小球，则“激光致冷”与下述的力学模型很类似：一辆质量为m的小车（一侧固定一轻弹簧），如图所示，以速度v0水平向右运动，一个动量大小为p，质量可以忽略的小球水平向左射入小车并压缩弹簧至最短，接着被锁定一段时间Δt，再解除锁定使小球以大小相同的动量p水平向右弹出，紧接着不断重复上述过程，最终小车将停下来．设地面和车厢均光滑，除了锁定时间Δt外，不计小球在小车上运动和弹簧压缩和伸长的时间．求：
（1）小球第一次入射后再弹出时，小车的速度大小和这一过程中小车动能的减少量；
（2）从小球第一次入射开始到小车停止运动所经历的时间．

参考答案：解：（1）小球射入小车和从小车中弹出的过程中，小车和小球所组成的系统动量守恒
由动量守恒定律可得：mv0－p＝mv1"，mv1"＝mv1+ p
解得：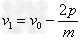
此过程中小车动能减少量
解得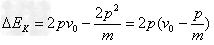
（2）小球第二次入射和弹出的过程及以后重复进行的过程中，同样有小车和小球组成的系统动量守恒
由动量守恒定律，得：mv1－p＝mv2"，mv2"＝mv2+ p
解得：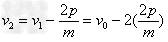
同理可推得：
要使小车停下来，即vn＝0，小球重复入射和弹出的次数为：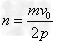
故小车从开始运动到停下来所经历的时间为：

本题解析：

本题难度：一般

3、简答题  

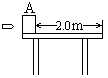
如图所示，水平桌面上有一木块A，质量198g，它与桌面间动摩擦因数为0.1，木块A距桌边2.0m，一子弹质量2.0g，水平射入木块后与木块一起在桌面上滑动，问子弹速度至少多大才能将木块击出桌面?

参考答案：
200m/s

本题解析：

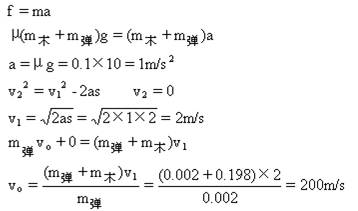
本题难度：简单

4、简答题  如图所示，质量m1=2.0kg的木板AB静止在水平面上，木板的左侧有一个固定的半径R=0.60m的四分之一圆弧形轨道，轨道末端的切线水平，轨道与木板靠在一起，且末端高度与木板高度相同．现将质量m2=1.0kg可视为质点的小木块C，从圆弧形轨道顶端由静止释放，小木块C到达圆弧形轨道底端时的速度v0=3.0m/s．之后小木块C滑上木板AB并带动木板AB运动，当小木块C离开木板AB右端B时，木板AB的速度v1=0.5
m/s，在小木块C在木板AB上滑行的过程中，小木块C与木板AB总共损失的动能△E=2.25J．小木块C与木板AB间的动摩擦因数μ=0.1．木板AB与地面间的摩擦及空气阻力可忽略不计．取g=10m/s2．求
（1）小木块C运动到圆弧形轨道末端时所受支持力的大小；
（2）小木块C在圆弧形轨道上下滑过程中克服摩擦力所做的功；
（3）小木块C在木板AB上运动过程中，小木块C相对于地面的位移．

参考答案：（1）小木块通过圆弧形轨道末端时，
由牛顿第二定律得：F-m2g=m2v20R，
解得小木块受到的支持力：F=25N；
（2）小木块在圆弧形轨道上下滑过程中，
由动能定理得：m2gR-Wf=12m2v02-0，
解得克服摩擦力做的功Wf=1.5J；
（3）木块C与木板AB间的摩擦力f=μm2g，
由动能定理得：
对木板：fs1=12m1v12-0，
对小木块：-fs2=12m2（v22-v02），
木块与木板间的位移关系：s2=s1+L，
小木块与木板总共损失的动能△E=fL，
解得：s2=2.5m；
答：（1）小木块C运动到圆弧形轨道末端时所受支持力大小为25N；
（2）小木块C在圆弧形轨道上下滑过程中克服摩擦力所做的功为1.5J；
（3）小木块C在木板AB上运动过程中，小木块C相对于地面的位移为2.5m．

本题解析：

本题难度：一般

5、简答题  如图所示，光滑水平面上有A、B、C三个物块，其质量分别为mA=2.0kg，mB=1.0kg，mC=1.0kg．现用一轻弹簧将A、B两物块连接，并用力缓慢压缩弹簧使A、B两物块靠近，此过程外力做功108J（弹簧仍处于弹性限度内），然后同时释放A、B，弹簧开始逐渐变长，当弹簧刚好恢复原长时，C恰以4m/s的速度迎面与B发生碰撞并粘连在一起．求
（1）弹簧刚好恢复原长时（B与C碰撞前）A和B物块速度的大小？
（2）当弹簧第二次被压缩时，弹簧具有的最大弹性势能为多少？

参考答案：（1）弹簧刚好恢复原长时，A和B物块速度的大小分别为υA、υB．
由动量守恒定律有：0=mAυA-mBυB
此过程机械能守恒有：Ep=12mAυA2+12mBυB2
代入Ep=108J，解得：υA=6m/s，υB=12m/s，A的速度向右，B的速度向左．
（2）C与B碰撞时，C、B组成的系统动量守恒，设碰后B、C粘连时速度为υ′，则有：
mBυB-mCυC=（mB+mC）υ′，代入数据得υ′=4m/s，υ′的方向向左．
此后A和B、C组成的系统动量守恒，机械能守恒，当弹簧第二次压缩最短时，弹簧具有的弹性势能最大，设为Ep′，且此时A与B、C三者有相同的速度，设为υ，则有：
动量守恒：mAυA-（mB+mC）υ′=（mA+mB+mC）υ，
代入数据得υ=1m/s，υ的方向向右．?
机械能守恒：12mAυA2+12（mB+mC）υ′2=Ep′+12（mA+mB+mC）υ2，
代入数据得E′p=50J．
答：（1）弹簧刚好恢复原长时（B与C碰撞前）A的速度为6m/s，B物块速度大小12m/s．
（2）当弹簧第二次被压缩时，弹簧具有的最大弹性势能为50J．

本题解析：

本题难度：一般